基于商空间和支持向量机的滚动轴承故障智能诊断

张金凤, 李 雪, 杨 蕊, 李继猛

(1. 燕山大学 里仁学院, 河北 秦皇岛 066004; 2. 燕山大学 电气工程学院, 河北 秦皇岛 066004)

1 引 言

滚动轴承是组成旋转机械设备的重要部件,其健康状况直接关系到整个设备能否正常、平稳运行,因此对滚动轴承进行状态监测和故障诊断,提高滚动轴承的诊断精度,对保障工业安全生产、提高企业效益具有重要意义[1,2]。目前研究较多且广泛应用于轴承故障诊断的智能诊断方法主要有:基于支持向量机(support vector machine,SVM)的智能诊断方法、基于人工神经网络的智能诊断方法、基于专家系统的智能诊断方法等。其中,SVM采用结构风险最小化原则,通过构建最优超平面的办法来分类,具有结构简单、能够适应小样本分类的特点,可以巧妙地将样本由低维转化到高维,能够有效解决小样本、非线性、高维度的问题,且具有运算速度快、泛化能力强等优点[3,4]。商空间理论是一种重要的粒计算模型[5,6]。它将不同的粒度世界与数学上的商集概念统一起来,将不同的粒度用不同的商集来表示,致力于研究论域、属性、结构在不同粒度下的表示与性质,以及这些表示、性质之间的相互依存、相互转换关系[7]。商空间粒度和层次的思想可在不同的粒度下分析问题,得到问题各个角度、不同层面的求解信息。在求解综合复杂问题时,商空间可以将一个大问题分解成若干子问题,子问题还可以进一步分解为更小的子问题,通过系列子问题的求解,综合得到原有问题的解。这种基于商空间的问题求解方法,不仅可以降低问题求解的复杂度,而且得到的解决方案更精确、更全面。目前商空间理论已被逐渐应用于图像检索[8]、目标搜索[9]、数据挖掘[10]等方面,但在机械故障诊断领域的研究较少,亟待进一步挖掘和探讨。

考虑到滚动轴承故障智能诊断中存在的问题(即振动信号非平稳且多样,与故障相关的有效特征向量难以有效选取等),本文利用商空间粒度和分层的思想,在从振动数据提取的时域和频域特征中找出对分类最敏感有效的整体和局部特征,作为SVM的输入特征向量进行分类,并通过对不同特征向量得出的分类结果进行加权融合得到最终的诊断结果。最后,滚动轴承不同健康状态的振动数据验证了所提方法的有效性和实用性。

2 商空间的理论基础

用三元组(U,f,T)来描述一个问题,其中U表示问题的论域,即全体研究对象;f(*)表示论域的属性,用函数f:U→Y表示,Y可以是具体的实数,也可以是立体模型;T表示论域的结构,即论域中各元素之间的相互关系。当问题(U,f,T)和一个等价关系R给定后,就得到一个新问题([U],[f],[T]),其中[U]为论域U相对于等价关系R的商集;[f]为商属性函数,定义为[f]:[U]→Y;[T]为商结构[6]。新问题([U],[f],[T])称为原问题(U,f,T)相对于等价关系R的商空间。由商空间的定义可知,一个等价关系对应一个商空间划分,即对应一个粒度。

为了更好地实现“清晰粒度”与“模糊粒度”的转化,文献[11]将商空间理论与模糊集理论相结合,将商空间推广到模糊商空间理论:设R是U上的一个模糊等价关系,令Rλ={(x,y)|R(x,y)≥λ},0≤λ≤1,则Rλ是U上的一个普通等价关系,称为R的截关系。令等价关系Rλ对应的商空间为U(λ),则由不同的λ构成商空间链{U(λ)|0≤λ≤1},即构成一个对U的分层递阶结构[11]。

该定理表明,确定了模糊等价关系,即可通过模糊等价关系的截关系,即普通等价关系,生成对应的商空间,即一个粒度层,多个普通等价关系生成商空间链,即分层递阶的粒度层结构。

3 基于商空间的特征约简

在滚动轴承故障诊断中,常用振动数据的时域和频域统计特征来表示其特点,并将其作为智能诊断算法的输入向量进行分类识别。但这些特征数量多,且对数据特点的描述缺乏针对性,如果盲目地全部利用反而降低分类识别精度。因此,研究如何从众多的时域和频域特征中选取尽量少且有效的特征作为智能诊断算法的输入,对提高算法效率和诊断精度有重要意义。

因此,文中利用时频域统计特征构成原始振动数据(样本/论域U)的属性集合,基于商空间不同粒度可以观察问题不同细节的思想,对其进行约简。在较粗的粒度层上,商空间可以看到对整体数据敏感的特征;在较细的粒度层上,商空间可以看到对局部数据敏感的特征。通过综合不同粒度层的特征,实现对故障数据的准确识别与分类。

3.1 等价关系的确定

在商空间中进行粒度划分,首先确定等价关系。由于工程实际中很难直接寻找等价关系,这里采用欧氏距离确定样本间的相似关系,并将其转化为等价关系。

(1)

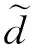
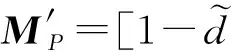
(2)

假设原始数据共包含N0种类别,以粒度层i上的样本作为一对象集合U,P为特征集合,由上述计算可得第i层的模糊等价关系矩阵R,粒度层i上的样本相对于特征集P的等价关系Rλ可定义为:

Rλ=mean(R)-s×(i-1)

(3)

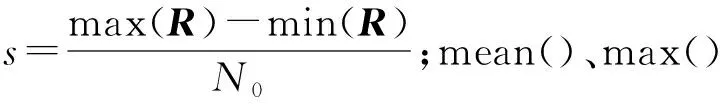
3.2 粒化分层与特征约简

一个等价关系对应一个商空间划分结果,即对应一个粒度层。特征约简是针对一个粒度层上的单个商集进行的。通过逐次计算不同特征加入后生成的等价关系对此商集进一步细化的影响,判断特征对商集的重要程度,约简出此商集的敏感特征。综合一个粒度层上所有商集的敏感特征,得到该粒度层的约简特征集。

文中以信息熵作为特征对商空间划分结果的评估指标,当增加某一特征后商空间划分结果差距越大,信息熵的改变越大,则表明该特征对该商空间论域样本的敏感度越高[14]。

给定一个论域U,P为U上的一个等价关系簇(特征集合),Xi为等价关系P对U进行划分得的一个商集,n为商集的个数,则信息熵H(P)定义为:

(4)

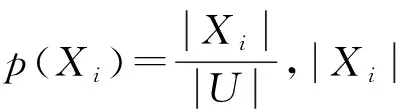
基于商空间的特征约简算法总体流程如图1所示,步骤描述如下:

1) 将初始的所有样本看成论域U,构成第一个粒度层,层数i=1,此粒度层只有一个商集,即论域U。

2) 对第i层上每一商集中的样本进行特征约简。特征约简之前,将所有样本的时频域特征按照距离评估法[15]进行评估,并按评估因子由大到小降序排序。

假定由若干样本构成的一商集U,A为所有时频域特征构成的初始特征集合,P为U上的一个特征集合,P⊆A且设置初始值P=∅:

a) 将初始属性集合A中距离评估因子最大的特征赋给特征集P,计算等价关系Rλ,并利用Rλ将商集划分到不同的子商集,计算划分结果的信息熵HP。

b) 将其余特征aj(aj∈A但aj∉P)依次与特征集P组合成特征集(P,aj),重新计算等价关系并进行分析,计算划分结果的信息熵HP,j,得到特征aj的重要度S(aj)=|HP,j-HP|。

d) 判断S(ak)是否小于设定值δ。若满足则停止约简,此时的特征集P即为该商集的敏感特征集;否则将ak加入特征集P=P∪ak,转到b),继续执行。

通过特征约简算法可得到该商集的约简特征集P以及基于特征集P得到的商集划分结果。组合各个商集的约简特征集,形成第i层的约简特征集,并进行输出;叠加各个商集中样本的划分结果,得到该层样本的所有子商集,假设共有m个子商集。

3) 终止条件判定,判断m个子商集中的样本个数是否都小于设定值σ。若所有商集均满足终止条件,则停止迭代,粒度层不再增加;若部分满足终止条件,将不满足终止条件的商集提取出来,组成一个更高的粒度层,层数为i=i+1,返回第2)步。图1中左边是同一粒度层的约简过程,最后得到该粒度层的约简特征集;右边是下一粒度层的判断和产生过程,得到商空间粒度层次结构。

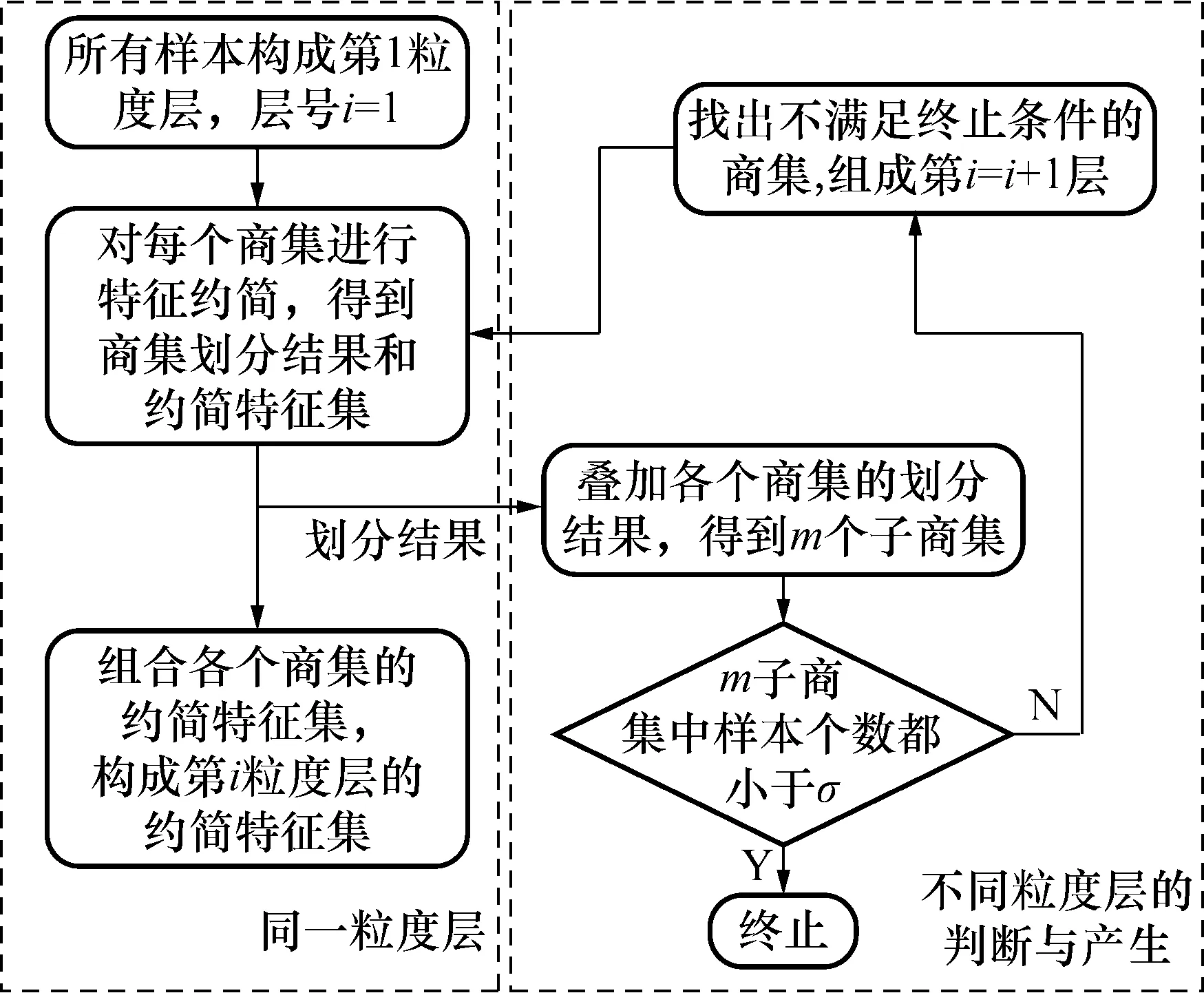
图1 基于商空间的特征约简流程Fig.1 The feature reduction process based on quotient space

基于商空间的特征约简方法,第一个粒度层以全体样本作为论域,约简出的特征代表整体样本的特点。其余粒度层都是部分样本作为论域,约简出的特征更能体现局部样本的特点,对部分故障类识别更有效。

4 基于商空间和SVM的智能诊断模型

运用基于商空间的特征约简方法,利用SVM对小样本问题决策的优良性能,构建基于商空间和SVM的滚动轴承故障智能诊断模型,如图2所示,主要步骤为:

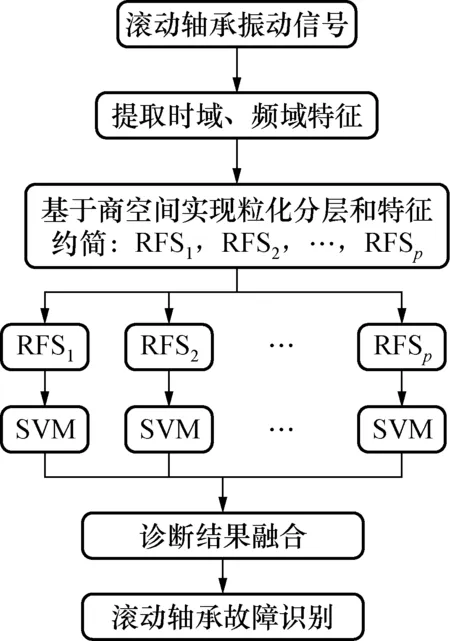
图2 基于商空间的智能诊断模型Fig.2 The intelligent diagnosis model based on quotient space

1) 数据采集和特征提取。采集滚动轴承的振动信号,构成初始论域U,并分为训练和测试两部分;提取振动信号的时域、频域特征构成初始特征集合A。将初始论域和初始特征集输入诊断模型。

2) 粒化分层与特征约简。利用训练样本,按照图1所示的特征约简流程,通过判断各个特征对商集划分的敏感度,约简得到每个粒度层的约简特征集RFS1,RFS2,…,RFSp。

3) 训练SVM分类器。利用每个粒度层约简出的特征集分别训练SVM分类器,p个粒度层共训练得到p个SVM分类器。将训练好的SVM用于测试集进行分类。

4) 测试样本诊断结果融合。根据分类器对训练样本每种故障的分类准确率和错误率确定各分类器结果的权值,采用加权投票的方法[16]将所有测试样本分类结果进行融合,得到各测试样本的诊断结果。

假定训练样本X={X1,X2,…,XN0},其中,N0为故障类别数,n为每一故障类的样本数。分类器i对训练样本X分类,设分到第j类的样本中,实际为第j类的样本数为b,误分样本数为d,则分类器i对故障类j的权值为:

(5)

因为商空间粒化分层时每一层上的样本不同,约简出的特征也是对部分故障类的识别更有效,所以权值的设定充分考虑了分类器对单个故障类的诊断效果,与商空间特征约简的特点相匹配。

4 实验验证

为验证所建模型的有效性,本文采用滚动轴承疲劳寿命试验台的轴承全寿命数据对所提方法进行分析。试验中选择的测试轴承为天马30311圆锥滚子轴承,加载轴承为天马N312圆柱滚子轴承。在试验过程中,采样频率为12 kHz,每隔5 min采集一次数据计算一个均方根值,则全过程得到的所有均方根值的变化趋势如图3所示。

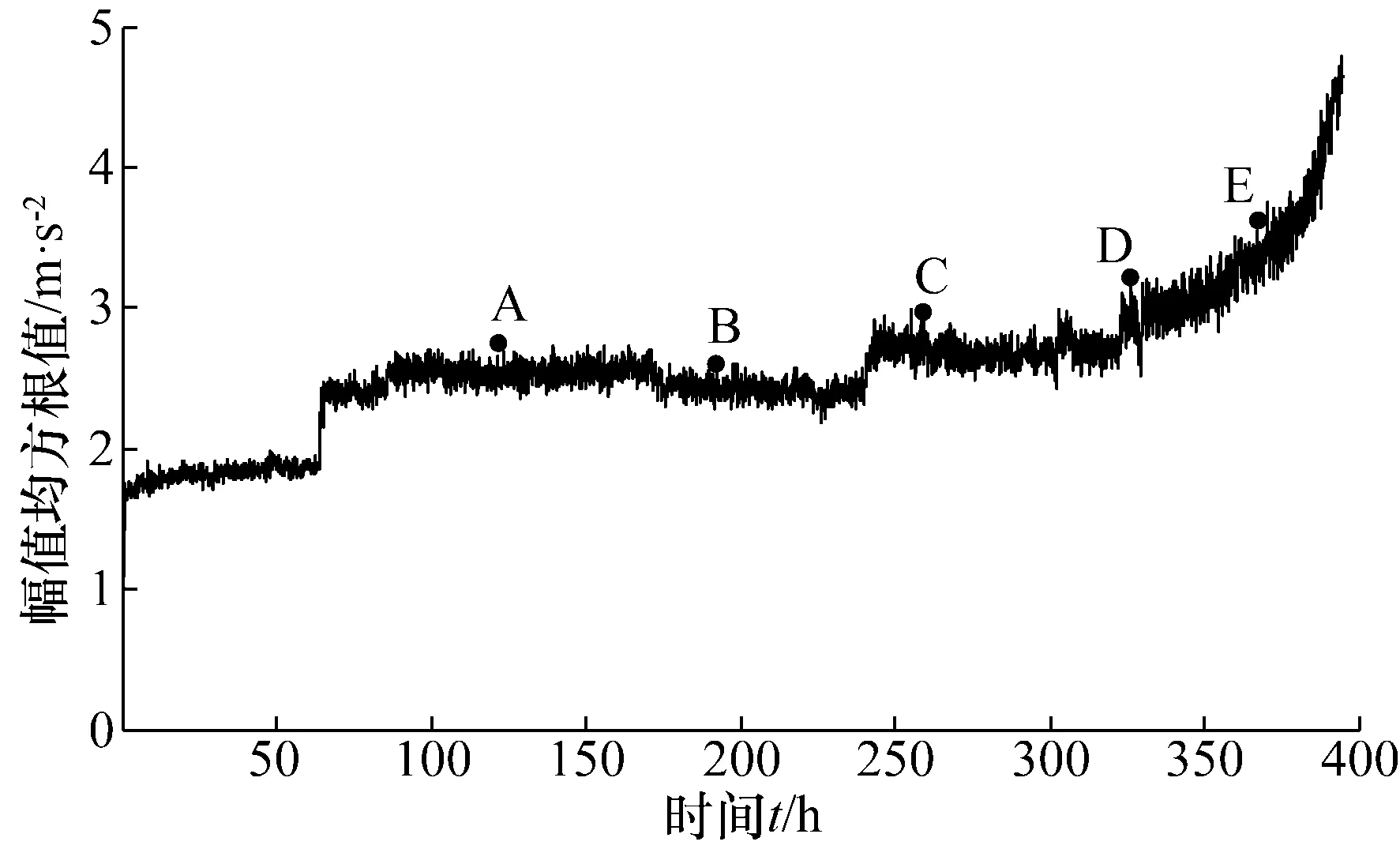
图3 滚动轴承实验全过程均方根值变化趋势图Fig.3 The change trend of RMS in the rolling bearing test process

依据滚动轴承在整个试验过程中均方根值的变化趋势,选取5个不同阶段(图3中A、B、C、D和E)的状态数据分别命名为工况1、工况2、工况3、工况4和工况5,用以表示滚动轴承在全寿命过程中的不同健康状态。每种状态数据采集28个样本,样本长度8 192。数据参数如表1所示,5种状态下滚动轴承的原始振动信号如图4所示。

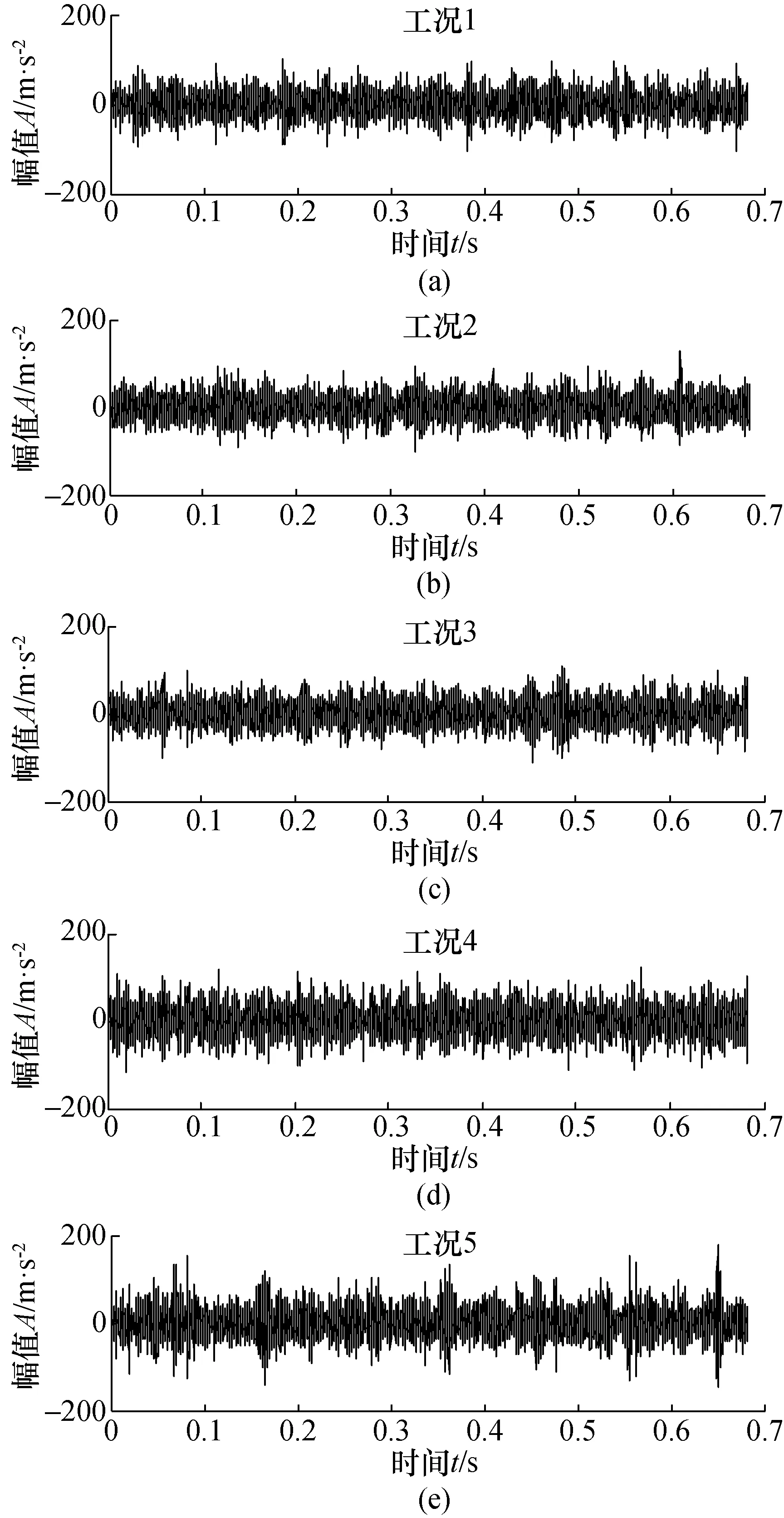
图4 5种状态下滚动轴承振动信号的时域波形Fig.4 Time domain waveform of vibration signal of Rolling bearing for 5 working conditions

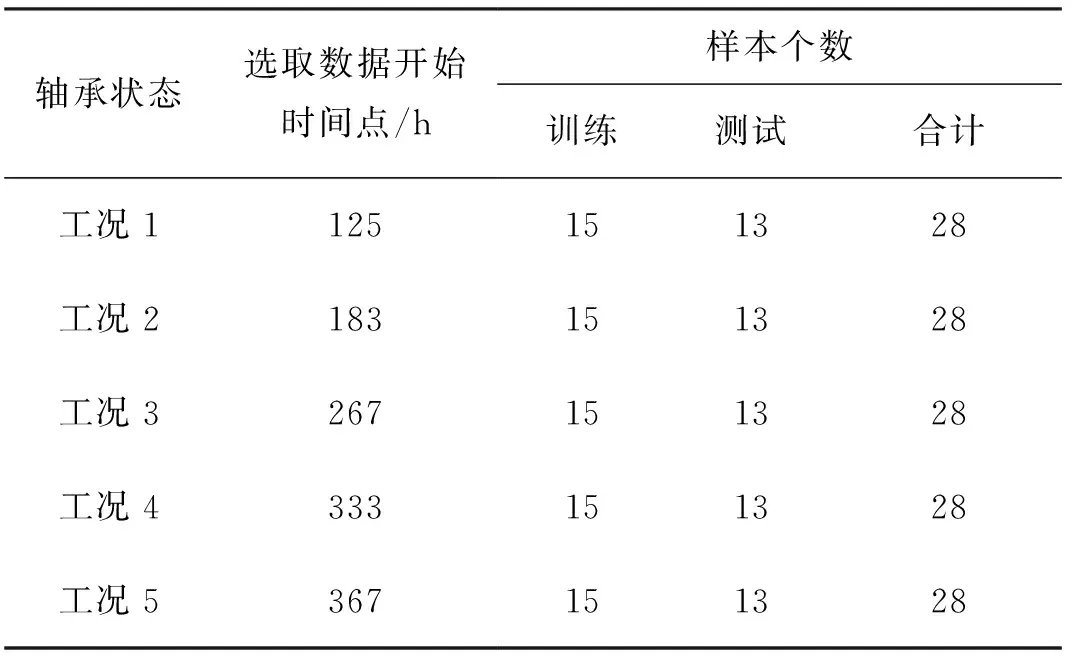
表1 轴承疲劳寿命实验5种工况Tab.1 5 working conditions of bearing fatigue life test

表2 时域、频域特征及计算公式Tab.2 Time and frequency domain features and calculation formula

2) 粒化分层和特征约简:设特征约简终止条件中的参数δ为0.65,分层终止条件中的参数σ设为12,即每个工况训练样本个数15的80%。运用特征约简算法,最终将所有训练样本划分为3个粒度层,每个粒度层约简得到的特征集如表3所示。

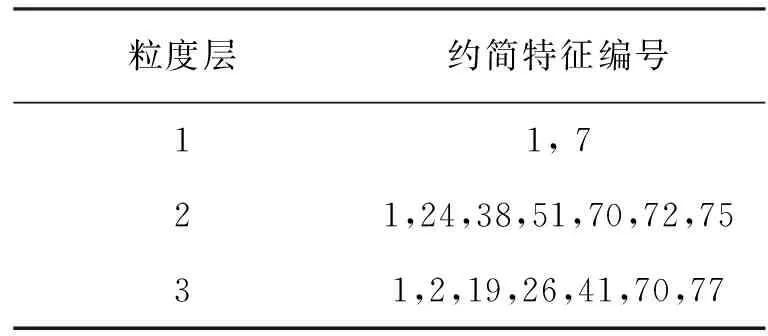
表3 各个粒度层上的约简特征集Tab.3 Reduced feature set of each granularity layer

3) 分类器分类与加权融合:利用训练样本产生的约简特征集训练一对多多分类SVM。SVM的参数如下:核函数类型kernel=‘gauss’,惩罚因子C=100,核函数宽度width=0.4。把每一层约简得到的特征集分别输入SVM进行训练,并对测试样本进行分类。采用加权投票法将3层的诊断结果进行融合,得到的分类结果如图5所示。作为对比,文中分别采用基于距离评估法选取的前16(3个粒度层共约简出16个特征)个特征和所有特征作为SVM的输入特征向量,对所有样本进行训练和测试,得到的分类结果如图6所示(这2种方法得到的分类结果相同)。可以看出,在图5中,有2个样本被错分到其它类别,而在图6中,有4个样本被错分。

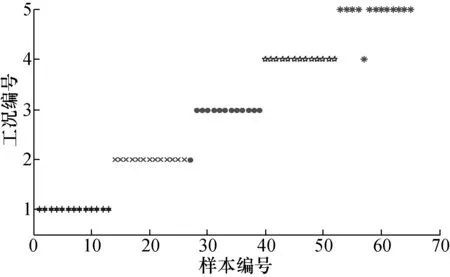
图5 基于商空间的智能诊断模型测试样本分类结果Fig.5 The test sample classification result based on quotient space intelligent diagnosis model

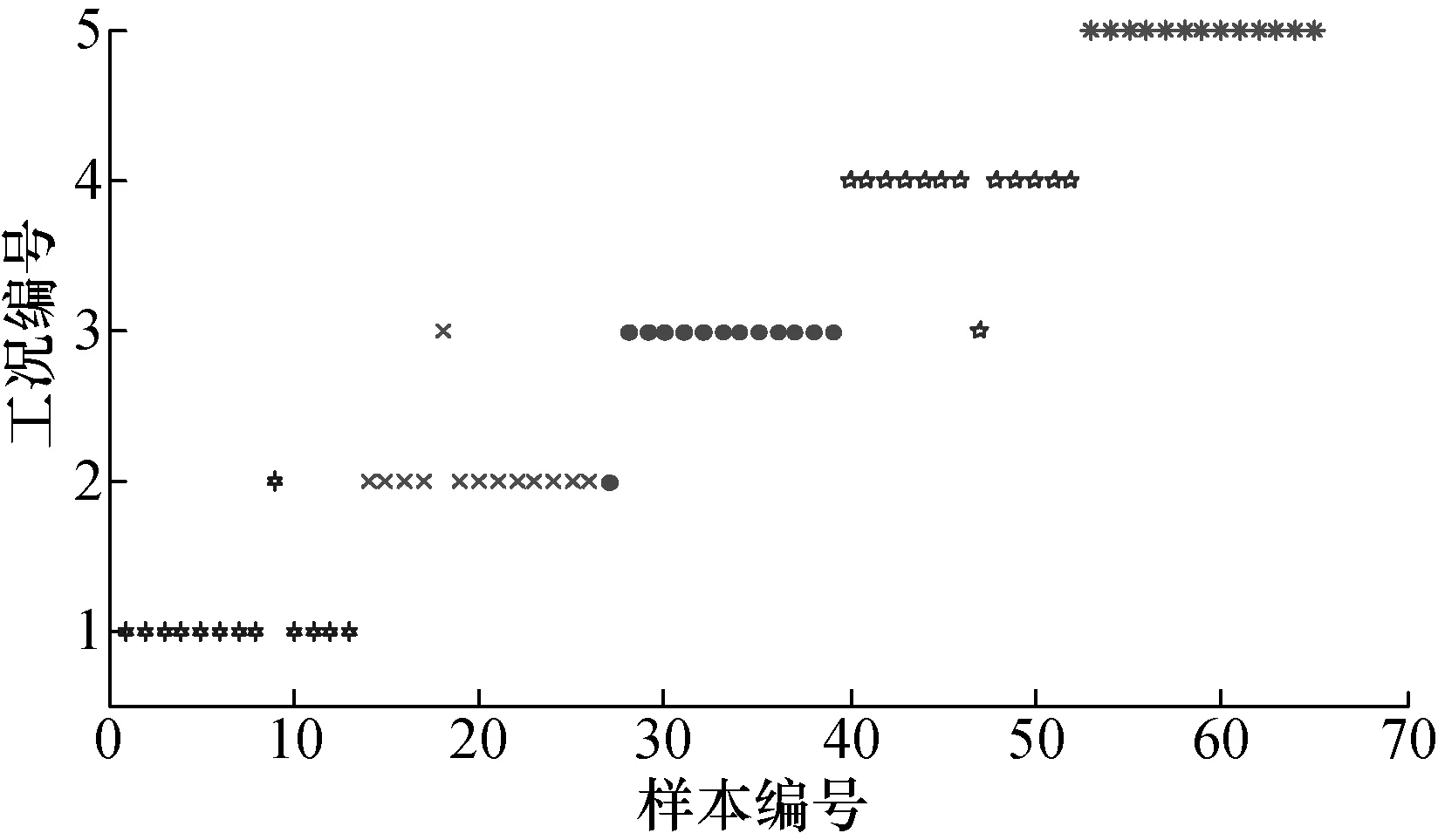
图6 基于距离评估法的测试样本分类结果Fig.6 The test sample classification result based on distance assessment

表4给出了3种方法的分类精度的对比结果。可以看出,运用基于商空间的智能诊断模型得到的最终诊断精度为96.92%,比单个粒度层的最高诊断精度(93.85%)高约3%。而利用基于距离评估法选取的前16个特征得到的分类精度是93.85%,利用所有特征向量去分类得到的诊断精度也是93.85%,均比商空间方法的诊断精度低约3%。由对比结果可以看出,基于商空间粒化分层思想的特征约简方法得到的特征对分类更敏感、更有效。同时也说明,基于商空间粒化分层思想约简出的特征集,代表了每一粒度层上不同样本的敏感特征,对部分样本的识别更精确。加权投票法的权值设定充分考虑了每一粒度层上SVM对每种健康状态的分类准确度,最终获取了较高诊断精度,实现了不同粒度层的融合。

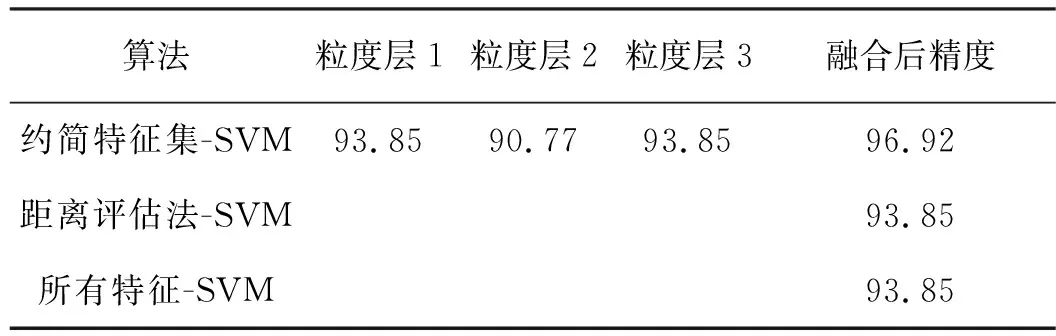
表4 分类精度对比Tab.4 Comparison results of classification accuracy (%)

5 结束语

本文提出了一种基于商空间和支持向量机的智能诊断模型,利用滚动轴承疲劳寿命试验数据验证了模型的有效性和实用性,并得出以下结论:

1) 基于商空间的粒度分层思想,将原始数据特征集合进行不同粒度层的特征筛选,分别作为支持向量机的输入特征向量,避免了输入特征向量过多且冗余对支持向量机分类精度的影响;

2) 将不同粒度层的支持向量机分类结果进行加权融合,提高了识别精度,改善了支持向量机对滚动轴承故障状态多分类问题的诊断性能;

3) 商空间粒化分层并集成的思想能够从不同角度、不同层面分析问题,通过合理的信息集成,得到解决方案。商空间在处理综合复杂问题方面具有独特优势,在故障智能诊断领域具有一定的研究价值和应用前景。