一道高考题的溯源与探究

丁春年

(甘肃省武威第十八中学，733000)

一、考题呈现与解法探究

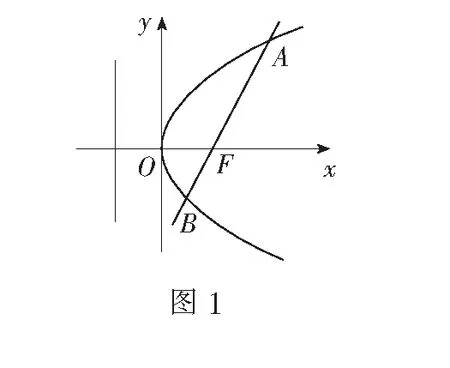
题目(2018年全国高考题)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A，B两点,|AB|=8.

(1) 求l的方程;

(2) 求过点A，B且与C的准线相切的圆的方程.

解(1)解法1由题意得F(1,0),可设直线l的方程为y=k(x-1),交点A(x1,y1)，B(x2,y2).

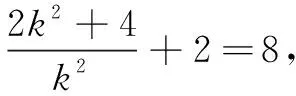
综上,直线l的方程为y=x-1.

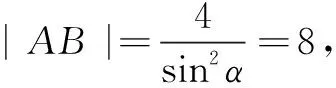
评注解法1是常规方法,解法2运用了抛物线焦点弦性质中的弦长公式,使得解答过程简洁明了.在实际应用中需要注意的是应用公式求解的方法适用于选择题或填空题,但在解答题中应用时需先证明公式.

(2) 由(1)知x1+x2=6,故弦AB的中点坐标为(3,2),直线AB的垂直平分线方程为y=-x+5.

评注上述解法是解析几何中求圆的方程的常规解法,若根据抛物线的焦点弦性质:以AB为直径的圆与抛物线的准线相切,易知所求圆的圆心为(3,2),半径为4,便可得出圆的一个方程,但这样做会漏掉另一个圆.

二、考题溯源

高考试题凝聚了命题人的智慧和心血.试题虽然新颖多变,但万变不离其宗,往往是源于课本而又高于课本,其切入点常常采用课本上的例题、习题或者阅读材料.上述考题就来源于人教A版选修2-1第81页复习参考题B组第7题:

习题过抛物线y2=2px(p>0)的焦点F作直线与抛物线交于A，B两点,以AB为直径画圆,借助信息技术工具,观察它与抛物线的准线l的关系,你能得到什么结论?相应于椭圆、双曲线如何?你能证明你的结论吗?

探究1过抛物线C:y2=2px(p>0)焦点F的直线与C交于A，B两点,则有

(1) 以AB为直径的圆与抛物线的准线l相切;

(2) 以AF或BF为直径的圆皆与y轴相切.

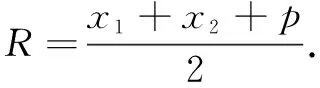
(2) 证明过程类似,从略.

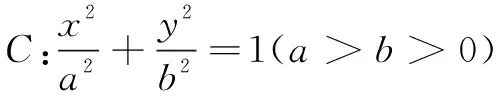
于是，|AB|=|AF|+|BF|=-e(x1+x2)-2a,从而以AB为直径的圆的半径R=-ex0-a.

三、高考链接

例1(2013年全国高考题)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5，若以MF为直径的圆过点A(0,2),则C的方程为( )

(A)y2=4x或y2=8x

(B)y2=2x或y2=8x

(C)y2=4x或y2=16x

(D)y2=2x或y2=16x

例2(2018年全国高考题)已知定点M(-1,1)和抛物线C:y2=4x,过抛物线C的焦点且斜率为k的直线与C交于A，B两点,若∠AMB=90°,则k=______.

解由题意,可设A(x1,y1)，B(x2,y2),且直线AB的方程为x=my+1.

由∠AMB=90°,可知点M在以AB为直径的圆上;又点M(-1,1)在C的准线上,由探究1知点M是以AB为直径的圆与抛物线的准线相切的切点,故y1+y2=2,得k=2.

综上所述，我们的高三复习备考应该立足于教材,而不是立足于复习资料.立足教材,不是把学过的教材拿过来重新学一遍,而是要对教材进行挖掘,科学整合教材中的例题、习题及其它材料,充分挖掘课本例题、习题的潜在教学功能,做到以少胜多,举一反三,这样才能提高学生的数学核心素养,培养学生的数学能力.