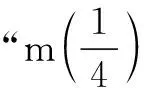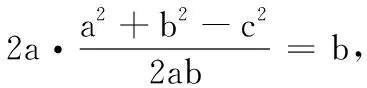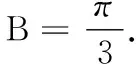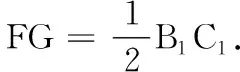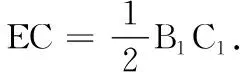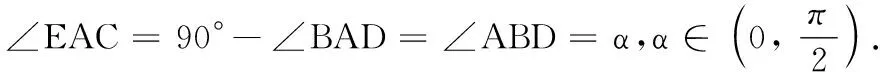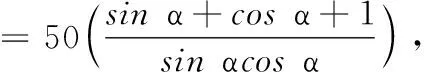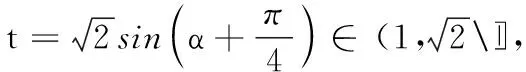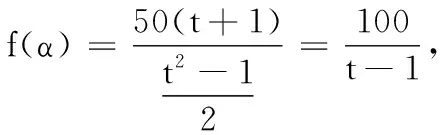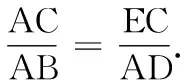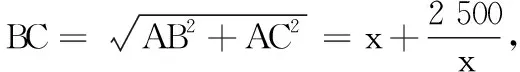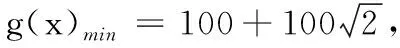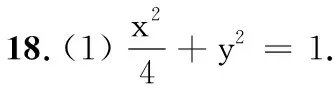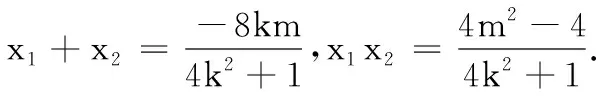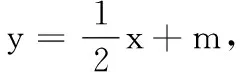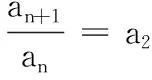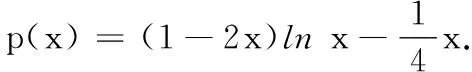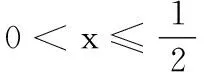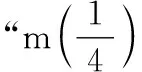高三数学综合测试

一、填空题(本大题共14小题，每小题5分，计70分)

1.已知集合M={-2,-1, 0, 1},N={x|x2+x≤0},则M∩N=______.

3.某同学5次数学练习的得分依次为114,116,114,114,117,则这5次得分的方差是______.

4.根据如图所示的伪代码,当输入的x为-1时,最后输出的m的值是______.

6.某同学参加“新冠肺炎防疫知识”答题竞赛活动,需从4道题中随机抽取2道作答.若该同学会其中的3道题,则抽到的2道题他都会的概率是______.

8.已知两非零向量b与a的夹角为120°,且|a|=2,|2a+b|=4,则|b|=______.

10.在平面直角坐标系xOy中,已知过定点(-10, 0)的圆M与圆x2+y2-6x-6y=0相切于原点,则圆M的半径是______.

12.已知函数f(x)=logax(a>1)的图象与直线y=k(x-1)(k∈R)相交.若其中一个交点的纵坐标为1,则k+a的最小值是______.

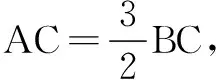
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)在斜三角形ABC中,角A,B,C的对边分别为a,b,c.

(1)若2acosC=b,且sin2C=sinAsinB,求B的值;

(2)若cos(2A+B)+3cosB=0,试求tanAtanC的值.

16.(本小题满分14分)如图,在三棱柱ABC-A1B1C1中,平面ACC1A1⊥平面BCC1B1,侧面BCC1B1是矩形,点E,F分别为BC,A1B1的中点.求证:

(1)BC⊥AC1;

(2)EF∥平面ACC1A1.

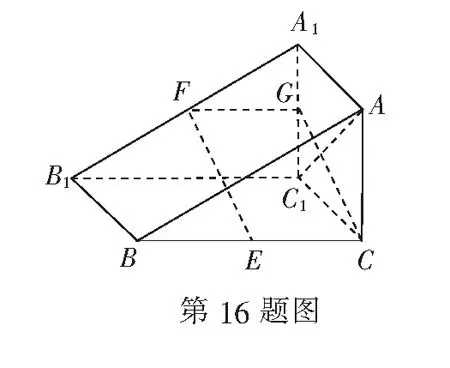
17.(本小题满分14分)如图,某森林公园内有一条宽为100米的笔直的河道(假设河道足够长),现拟在河道内围出一块直角三角形区域养殖观赏鱼.三角形区域记为∆ABC,A到河两岸的距离AE,AD相等,B,C分别在两岸上,AB⊥AC.为方便游客观赏,拟围绕∆ABC区域在水面搭建景观桥.为了使桥的总长度l(即∆ABC的周长)最短,工程师设计了以下两种方案:

方案1设∠ABD=α,求出l关于α的函数解析式f(α),并求出f(α)的最小值.

方案2设EC=x米,求出l关于x的函数解析式g(x),并求出g(x)的最小值. 请从以上两种方案中自选一种解答.(注:如果选用了两种方案解答,则按第一种解答计分)

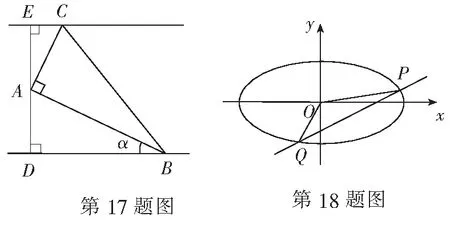
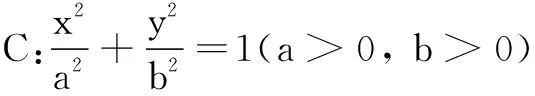
(1)求椭圆C的标准方程；

(2)直线l:y=kx+m(k>0,m≠0)与椭圆C交于P,Q两点,设直线OP,OQ的斜率分别为k1,k2.已知k2=k1k2.

① 求k的值;

② 当∆OPQ的面积最大时,求直线PQ的方程.

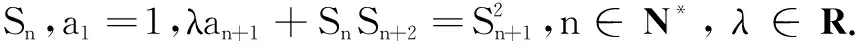
(1)若λ=-3,a2=-1,求a3的值；

(2)若数列{an}的前k项成公差不为0的等差数列,求k的最大值；

(3) 若a2>0,是否存在λ∈R,使{an}为等比数列?若存在,求出所有符合题意的λ的值;若不存在,请说明理由.

20.(本小题满分16分)对于定义在D上的函数f(x),若存在k∈R,使f(x)

(1)设函数h1(x)=f(x)+1(x≥1).若a=0,且h1(x)为“m(k)型函数”,求k的取值范围;

附加题

21.【选做题】本题包括A，B，C三小题,请选定其中两题作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.

(1)求矩阵A;

C.(本小题满分10分)若实数x,y,z满足x+2y+3z=1,求x2+y2+z2的最小值.

【必做题】(第22，23题,每小题10分,计20分.解答时应写出文字说明、证明过程或演算步骤.)

(1)求抛物线的方程；

(2)设线段AB的垂直平分线交x轴于点T.

① 证明:y1y2为定值;

② 若OA∥TB,求直线l的斜率.

23.(本小题满分10分)设n∈N*,k∈N,n≥k.

参考答案

一、填空题

二、解答题

(2)由cos(2A+B)+3cosB=0,可得cos[π+(A-C)]+3cos[π-(A+C)]=0,所以cos(A-C)=-3cos(A+C),整理可得2cosAcosC=sinAsinC,故tanAtanC=2.

16.(1)由侧面BCC1B1是矩形,得BC⊥CC1.

因为平面ACC1A1⊥平面BCC1B1,平面ACC1A1∩平面BCC1B1=C1C,BC⊂平面BCC1B1,所以BC⊥平面ACC1A1.

因为AC1⊂平面ACC1A1,所以BC⊥AC1.

(2)取A1C1的中点G,连结FG,CG.

所以EC∥FG,且EC=FG. 所以四边形EFGC为平行四边形,EF∥GC.

又EF⊄面ACC1A1,GC⊂面ACC1A1,所以EF∥平面ACC1A1.

(2)因为x>0,

(2)由前k项成等差数列,设公差为d,则a2=1+d,a3=1+2d.

d2+d+1=λ(1+d).

①

3d2+2d+1=λ(1+2d).

②

②-①，得2d2+d=λd,即2d+1=λ,代入① ，得d2+2d=0,所以d=-2,λ=-3.

所以k=4符合题意.

若k=5,则a1=1,a2=-1,a3=-3,a4=-5,a5=-7,S3=-3,S4=-8,S5=-15.

(3)假设存在λ∈R,使{an}为等比数列,设前3项分别为1,q,q2,则S1=1,S2=1+q,S3=1+q+q2.在(*)式中令n=1， 得λq+(1+q+q2)=(1+q)2,化简得q(λ-1)=0.由q=a2>0,得λ=1.

Sn+1(Sn+1-1)=Sn(Sn+2-1).

(**)

C.由柯西不等式,得(x+2y+3z)2≤(12+22+32)(x2+y2+z2),即

所以，抛物线的方程为y2=x.

所以kAM=±1,即直线l的斜率为±1.