从相似结构中寻找解题思路

丁正东

(江苏省泰州市姜堰区溱潼中学，225508)

解题过程是知识积累重现及再创造的过程,这其中的经验积累需要足够丰富.联想熟悉的数学结构模型,使之能够建立联系的切合点,是解题中最常用的手法之一.观察问题的角度不同,同一线索的数学结构模型认知就会不同,解题方法就会有所不同,这也是一题多解之源.本文通过一道压轴填空题的解法探究,展示结构分析在思路寻求中的引导作用.

一、试题呈现

题目在平面直角坐标系xOy中,已知点A(x1,y1),B(x2,y2)在圆O:x2+y2=4上,且满足x1x2+y1y2=-2,则x1+x2+y1+y2的最小值是______.

二、解法探究

解法1向量结构+圆的参数方程

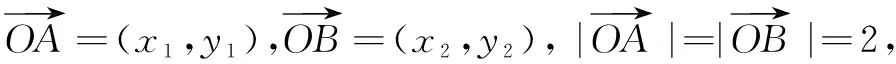
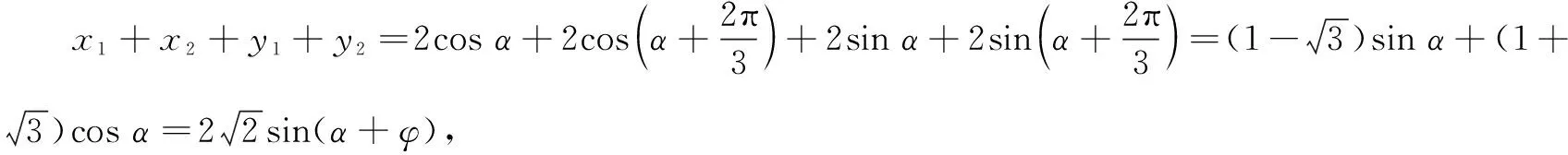
解法2向量结构+中点公式

解法3参数方程+中点公式

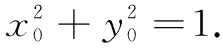
解法4中点公式+不等式法

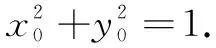
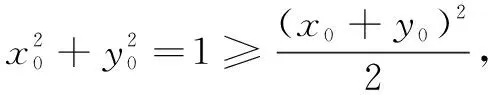
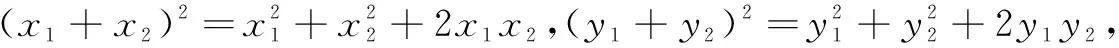
设x1+x2=2cosα,y1+y2=2sinα,α∈[0,2π),则可得

x1+x2+y1+y2

=2(sinα+cosα)

评注解法5在代数结构上虽然是从完全平方的联想开始,但本质上是利用了后续的圆参数方程及asinα+bcosα的结构形式,这也提醒我们综合性解题能力的培养在数学核心素养提升方面的重要性.当然，x1x2与x1+x2在结构上还可以往韦达定理的方向进行探讨.