小题纠偏的再纠偏

陆琳琳

(浙江省东阳市第二高级中学,322100)

光明出版社出版的2020新课标高考总复习《三维设计》第32页,在介绍了对数与对数函数的基本知识后,给出了如下一个小题纠偏题.

题目函数f(x)=log(x+1)(2x-1)的单调递增区间是______.

一、原题分析纠偏

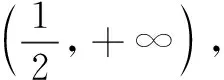
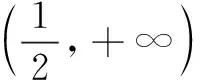
上述推理看似完美无缺,但仔细推敲却不符合逻辑.由于对数函数的底数为常数,当一个对数型函数的底数、真数都有变量时,直接用对数函数的性质进行如上简单处理不能令人信服.笔者利用换底公式对函数进行转化,并利用导数法研究f(x)的性质,发现原题的参考答案及上述推理确实是错误的.

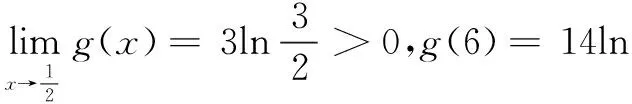
二、探究与改编

从上述解答过程可以发现x0是无法求出其精确值的,故该题作为填空题,属于无法给出准确答案的“错题”.笔者通过研究,给出以下两种修改方案.

首先利用换元,令t=x+1,将问题转化为求函数f(t)=logt(2t-3)的单调区间.

方案1寻找恰当的b,使函数f1(t)=logt(2t+b)的单调区间能求.

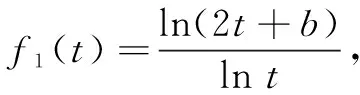
令g(t)=2tlnt-(2t+b)ln(2t+b),则

g′(t)=2lnt-2ln(2t+b).

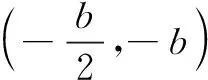
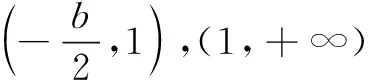
(ii)若b<-1,则g(t)max>0,此时方程g(t)=0的根无法解出.

(3)当b=0时, 易见g′(t)<0,f1(t)在(0,+∞)单调减.

改编题1函数f(x)=log(x+1)(2x+5)的单调减区间是______.

方案2寻找恰当的a,使f2(t)=logt(at-3)的单调区间能求.

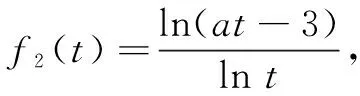
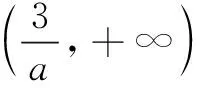
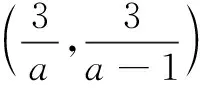
(ii)若10,此时h(t)=0的根无法解出.

(3)当a=1时,易见f2(t)在(3,+∞)单调增.

改编题4函数f(x)=log(x+1)(5x+2)的单调递减区间是______.

三、总结与反思

在高三的教与学过程中,我们偶尔会遇到错题.此时,师生可以通过探究、改编活动培养我们发现问题和解决问题的能力,从而激发学生学习数学的兴趣和向权威挑战的勇气.要切实转变教与学的理念,把学生从“学数学”的意识转到到“做数学”的意识上来,既要注重学习的结果,更要注重学习的过程,全面发展学生的数学核心素养.