例谈用“设而不求”法解决与隐零点相关的问题
2020-08-06邓辉
邓 辉
(江苏省无锡市北高级中学,214000)
近几年的高考压轴题中,用导数解决函数综合问题已成为命题的趋势.用导数解决函数综合问题,最终都会归结于函数的单调性的判断,而函数的单调性又与导函数的零点有着密切的联系.但是有很多导函数零点无法直接求出,我们称之为导函数的隐零点.本文将用“设而不求”的方法来探究相关问题的处理策略.
一、证明不等式问题
例1已知函数f(x)=lnx+x,g(x)=xex-1,求证:f(x)≤g(x).
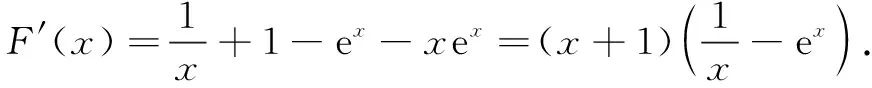

当x∈(0,x0)时,G(x)>0,F′(x)>0,F(x)为增函数;当x∈(x0,+∞)时,G(x)<0,F′(x)<0,F(x)为减函数.故F(x)≤F(x0)=lnx0+x0-x0ex0+1.


二、求含参不等式的参数的范围问题
例2已知函数f(x)=ax+xlnx(a∈R).
(1)若f(x)在[e,+∞)为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x-1) 解(1)依题意,f′(x)=a+lnx+1≥0在区间[e,+∞)恒成立,故a≥(-lnx-1)max=-2,即a的取值范围是[-2,+∞). 于是,当1 综上,k 评注本题通过参数分离法将问题转化为求g(x)的最小值.其关键在于寻找g′(x)(即h(x))的零点x0,并利用零点定理缩小其范围,通过等式lnx0=x0-2化简g(x0),达到设而不求得出k的最值的目的. 例3已知函数f(x)=(x+1)lnx-ax+a(a为正实常数).若不等式(x-1)f(x)≥0恒成立,求a的取值范围. 当0 当a>2时,设m(x)=(x+1)2-2ax=x2+(2-2a)x+1,则Δ=4a(a-2)>0,m(x)=0有两根x1,x2(x1 综上,a的取值范围是(0,2]. 解法2对解法1进行优化.当a>2时,因为m(1)=4-2a<0,故存在x>1,使得m(x)=0.于是,当x∈(1,x0)时,m(x)<0,即h′(x)<0,h(x)单调递减,所以h(x0) 评注本题讨论参数a时,将函数f(x)变形为h(x),变形后lnx系数为1,使导函数变得简单,便于寻找导函数的隐零点.解法2通过虚设零点x0,简化了解法1找点的难度. 评注近几年的各省高考题中时常出现指数与对数的混合型问题.总体来说,这类问题比较难,我们要尽可能把指数和对数分开,通过虚设零点,设而不求,并利用指数式与对数式的转化达到简化计算、回避难点的目的. 隐性零点问题的解决运用的是数学中的“设而不求”思想,通过虚设零点、限制范围、整体代换,将目标变形为可求最值的函数,进而解决不等式恒成立证明、求参数范围等问题.




三、证明含有参数的不等式问题