面向数据驱动的城市轨道交通短时客流预测模型
2020-08-06梁强升许心越刘利强
梁强升,许心越,刘利强
(1.广州地铁集团有限公司 运营事业总部,广东 广州 510330;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
1 引 言
城市轨道交通以其运量大、速度快、可靠性高等运行特点,已成为人口密集大城市的首选交通方式[1]。我国城市轨道交通建设快速增长,诱发了客流的急剧上升[2],导致轨道交通拥挤、服务质量下降。因此,如何分析管理城市轨道交通客流,特别是把握客流的短时变化规律已成为运营管理者提高城市轨道交通运行效率、缓解拥堵、提高服务质量迫切需要解决的问题[3]。
城市轨道交通客流短时预测方法主要分为经典的统计模型和机器学习模型。经典的统计模型主要包括自回归综合移动平均(ARIMA)和指数平滑模型,在早期得到了广泛的应用[4]。例如,NI等[5]将线性回归和ARIMA 模型相结合对纽约地铁的短期客流进行了预测。WILLIAMS 等[6]基于季节ARIMA 模型预测交通流量。然而,这些统计方法大多属于线性的时间序列模型,无法捕捉客流的非线性变化,导致其进行短时客流预测的误差较大[7]。
为解决这一非线性预测难题,机器学习方法应运而生。机器学习方法包括支持向量机、贝叶斯网络、k-邻近算法、人工神经网络等。例如,SUN等[8]提出了一种小波-支持向量机混合方法对北京地铁系统的换乘客流进行预测。ROOS 等[9]提出了一种利用不完整历史观测数据预测短期客流的动态贝叶斯网络方法。JIAO等[10]提出了一种基于贝叶斯组合和非参数回归的改进卡尔曼滤波模型来预测北京地铁13 号线高峰时段的客流。WEI 等[11]将经验分解模式与前馈神经网络相结合对短期客流进行预测,结果表明该模型的预测精度优于ARI⁃MA 模型。LI 等[12]提出用径向基函数神经网络预测单站客流。然而,所有这些模型都基于浅层结构,无法捕获数据中的复杂非线性关系[13-14]。
近年来,循环神经网络、长短期记忆神经网络、门控递归单元神经网络和卷积神经网络由于在捕捉时空关系方面具有优越的性能而受到广泛重视[15-17]。在时间预测方面,循环神经网络利用输入序列和时间步长之间的连续反馈来获得时间相关性;而长短期记忆神经网络和门控递归单元神经网络,可以处理比循环神经网络更长的序列[18]。同时,长短期记忆神经网络和门控递归单元神经网络都可以借助门控机制解决循环神经网络中的梯度消失和梯度爆炸问题[17]。在空间预测方面,由于卷积神经网络的参数共享机制和连接稀疏性,使得卷积神经网络具有很好的空间信息特征。因此,结合长短期记忆神经网络、门控递归单元神经网络和卷积神经网络进行客流预测时,可以综合考虑客流的时空特征。例如,DU 等[19]提出一种深度不规则卷积残差长短期记忆神经网络对城市交通客流进行预测。DO 等[20]应用卷积神经网络和门控递归神经网络预测流量,该模型可以有效地提取动态时空特征。然而,这些既有的模型仅适用于单条线路的客流预测,无法考虑路网间的客流特征,难以实现对路网的客流预测。
近年来,一种擅长解决这类网络空间相关性问题的图卷积神经网络方法被提出,并得到了广泛关注。YU 等人[21]采用图卷积神经网络提取路网的空间相关性,从而对交通速度进行预测。虽然图卷积神经网络被证明具有较强的预测精度和可解释性,但如何结合城市轨道交通自动售检票系统(AFC)和时刻表数据利用图卷积神经网络方法进行短时客流预测的研究尚属空白。
综上,本文提出了一种新的融合循环门控单元的时空图卷积神经网络(GCGRU)模型来预测城市轨道交通的短时客流。本方法提出使用图卷积神经网络来描述短时客流的空间特征,特别是提出了基于旅行时间的邻接矩阵构建方法,并进一步融合循环门控单元描述客流间的时间特征,形成了考虑客流时空演化关系的城市轨道交通短时客流预测模型,具有较强的预测精度和可解释性。
2 数据驱动的短时客流预测方法
2.1 问题描述
设城市轨道交通网络用1 个加权有向图G=(V,E)表示:V为城市轨道交通车站集合,E为线路区间集合。设邻接矩阵为A,矩阵中各个元素的值代表每2 个站点间的旅行时间;设站点特征矩阵为X:其中X的行数N为站点数量,列数P为车站的特征属性(即时间步长)。历史进站量为每个车站的特征属性,xi是每个站点在第i个时间步长的进站量。
不同车站类型(枢纽、通勤、商业等)和土地性质差异会产生不同的客流导向,导致不同站点在不同时段有不同的客流特征。土地性质及站点类型等因素造成进出站量的变化,并可通过进站量来反映这些变化,因此进站量常被作为主要输入变量进行出站量的预测。
某一车站的客流经过列车运输分散到路网各个相关车站,不同车站的客流经过特定列车运输到达同一个目的车站,因此车站的进站客流会影响到其他车站的出站客流。本文根据城市轨道交通路网中各站点的历史进站量来预测未来的出站量。因此,城市轨道交通短时客流预测问题可转化为根据邻接矩阵A和节点的进站客流量特征矩阵X来学习映射函数f,即

2.2 面向数据驱动的短时客流预测模型
本节提出面向数据驱动的短时客流预测方法分为2 部分:①用来提取序列空间特征的图卷积神经网 络GCN (Graph Convolutional Networks)神经网络;②用来提取时间特征的门控递归单元神经网络GRU(Gate Recurrent Unit)神经网络。第1 部分的输出作为第2 部分GRU 的输入。具体模型框架如图1所示。

图1 模型框架
2.2.1 空间图卷积网络模型
图中G=(V,E)具有2 种特征:节点特征和结构特征(节点之间的依赖关系)。GCN 神经网络有2 种:一种基于顶点域或空间域,另一种基于频域或谱域。本文采用基于空间域的GCN 来学习图的结构特征。
GCN 模型有2 个输入:邻接矩阵A和进站客流特征矩阵X。邻接矩阵A的表达式为

式中:tij为乘客从车站i到车站j的平均旅行时间。
GCN 的层与层之间的传播方式可表示为

式中:H(l),H(l+1)分别为第l层和第(l+1)层的特征矩阵;g为斜坡激活函数;为邻接矩阵与单位矩阵的和,=A+I;为的度矩阵;W(l)为第l层的权矩阵。初始层H(0)的特征矩阵为进站客流量特征矩阵X,且g和可由下面公式计算

由于GCN 层的最佳数量是2~3,本文选取2层GCN模型,故可将式(3)重新表述为

2.2.2 GRU模型
GRU用以捕捉预测数据间的时间信息,它有2个门:更新门(表示为zt)和重置门(表示为rt),如图2所示。更新门决定了客流预测保留多少以前的状态,重置门决定了新输入与前一状态融合的程度。更新门的值越大,则前一个时间步长内的信息被带入的就越多。重置门的值越小,则前一时间步长内的信息越容易被忽略。

图2 GRU的计算图
GRU的输入用矩阵X′=[x′t-P+1,x′t-p+2,...,x′t]表示,是H(2)(GCN模型的输出)的转置矩阵。
每个GRU的状态计算如下。

式中:Wrh,Wrx,Wzh,Wzx,Whh,Whx为加权矩阵,控制着隐藏层到相应的输入的连接;ht-1为第t-1个时间步长的隐藏状态;br,bz,为偏置项;为当前记忆内容;ht是第t个时间步长的隐藏状态,也是GRU 的输出;σ是sigmoid 函数,σ和tanh 是由以下公式定义的非线性激活函数。

2.2.3 损失函数
在模型训练过程中,目标是城市轨道交通网络实际客流量与预测值之间的误差最小化,即模型的损失函数为

本文提出的模型具有以下优点:
(1)可以通过邻接矩阵学习城市轨道交通网络系统中各站点之间的空间相关性,解决了传统CNN 模型不能预测网络层次客流的问题。目前应用于道路网络层次的GCN 都是基于地理距离来构建邻接矩阵,而本文基于旅行时间来构建邻接矩阵,能更准确地学习各站点之间的空间关系。
(2)采用的GRU 模型通过更新门和重置门对历史客流信息进行筛选,以解决序列之间的依赖关系,实现对较长时间序列的精准预测。此外,GRU 中的2 个门控单元均采用了非线性函数,能够有效识别客流中的复杂非线性关系。
(3)本模型结合GCN和GRU模型可以实现城市轨道交通全网的时空客流预测,与传统只考虑时间关系的模型相比,本模型的预测精度更高、解释性更强。此外,本模型采用数据驱动的方法来学习城市轨道交通网络中的时空关系,具有较强的稳定性和鲁棒性。
3 预测模型及分析
3.1 数据描述
选取广州地铁6 个重要的就业型站点为例,对客流预测模型进行有效性验证。所选取的车站具有客流量较大或是重要的换乘站等特点,即:客村、杨箕、珠江新城、体育西路、公园前、琶洲,如图3所示。预测数据采用2017年5月15日至5月27日的广州地铁路网数据、AFC 数据(见表1)和时刻表数据,这些数据含周末的客流量。基于以上数据构建预测模型相关的2个矩阵。
(1)描述城市轨道交通车站间空间关系的6×6邻接矩阵。矩阵的行表示车站,矩阵中的值为乘客在站与站之间的平均旅行时间,可由时刻表数据确定。

图3 典型的广州地铁车站示意图
(2)描述每个车站进站和出站客流随时间变化的特征矩阵和标签矩阵。矩阵的行表示一个时间步长内各站点的客流量,列表示在不同时间段内各站点的客流量。其中:客流量是根据AFC 数据进行15 min粒度统计后的量。进一步利用最小-最大规范化技术,将矩阵内的数值规范化到[0,1]范围内。

表1 AFC数据样本
3.2 评价指标
选取均方根误差(SRMSE)、平均绝对误差(SMAE)、精度(SACC)、决定系数(R2)和可释方差得分(SVar)5 个评价指标来评价模型的性能,它们的计算公式如下。

在上述评价指标中,SRMSE和SMAE都是用来度量预测误差的,两者都是绝对指标,且值越小,预测性能越好。SACC,R2和SVar都是相对指标,值越大,预测性能越好。
3.3 参数调整
GCGRU 模型的超参数主要包括学习率、批大小、训练次数、隐藏单元数和正则化参数。在本次实验中,学习率初始值设为0.001,并用Adam 优化器自动优化;批量大小一般设置成2 的n次方,批量大小越大,模型精度越低、训练速度越快,通过手动调节并综合考虑精度和训练速度,最终将其设为64;当训练次数达到2 000 时,模型的精度不再上升,因此将训练次数设为2 000;将λ分别设定为0,0.1,0.01,0.001,0.001 5,0.002,当λ为0.001 5 时,模型精度达到最高,因此将λ设置为0.001 5。以上参数对模型5 个评价指标的影响都很小,因此不再进一步分析。
由于隐藏单元数对深度学习模型的5 个评价指标有很大的影响[14],因此本文对不同数量隐藏单元下的GCGRU 模型进行了实验(分别设定8,16,24,32),以获取最优的隐藏单元数。实验结果如图4所示。随着隐藏单元数的增加,SRMSE和SMAE先减少后增加,SACC,R2和SVar的值呈现相反的变化趋势。当隐藏单元数为24 时,SRMSE和SMAE达到最小,SACC,R2和SVar的值同时达到了最大。因此,最优的隐藏单元数为24。

图4 不同隐藏单元数下评价指标的变化
3.4 模型评价
选取以下模型作为基线模型进行对比分析。
(1)ARIMA 模型是典型的时间序列模型,擅于处理时间序列数据。该模型有3个整数型的参数p,d,q,该模型通过自动遍历不同的p,d,q组合,确定最优组合为:p=1,d=1,q=1。
(2)支持向量机(SVR):SVR 是经典的机器学习模型,它利用历史数据对模型进行训练,得到输入和输出之间的关系,因此常用于预测客流。选取带有线性核的SVR模型作为比较模型。
(3)前馈神经网络(BP): BP 模型是基本的神经网络模型,能够处理非线性关系。BP 模型有学习率(自动调节)、批量大小、训练次数、正则化系数λ以及隐藏单元数5 个参数,其调节过程与3.3节所叙方法一样。调参结果为:批量大小为64,训练次数为2 000,λ为0.001 5,隐藏单元数为24。
(4)GRU:GRU 是深度学习模型,具有捕捉时间信息的能力。GRU 的参数与BP模型一样,调节结果为:批量大小为64,训练次数为2 000,λ为0.001 5,隐藏单元数为24。
本文在不同预测步长下利用以上各种模型进行了客流预测,结果见表2。
3.4.1 整体预测结果
首先,将本文提出的GCGRU 模型与其余4 个模型(ARIMA,SVR,BP 和GRU 模型)的SRMSE进行了比较,不同模型的SRMSE比较结果如图5所示。对于15 min 的预测步长,GCGRU 的SRMSE分别比ARIMA,SVR,BP和GRU 模型的SRMSE降低了80.5%,77.4%,33.7%和28.9%。因此,本文提出的GCGRU 比4 个对比模型的预测误差都低。

图5 5个模型的均方根误差比较结果
其次,将GCGRU 模型与不具备时间信息捕捉能力的非线性模型(SVR 和BP 模型)进行了比较分析。从表2中可以看出,SVR 模型的SACC太小以至于可被忽略,因此,只将GCGRU 模型的精度SACC与BP 模型和GRU 模型进行对比,如图6所示。对于15 min 的预测步长,GCGRU 模型的SACC分别比BP 模型和GRU 模型的SACC提高了10.4%和8.1%。因此,本文提出的GCGRU 模型比SVR模型和BP模型的预测精度都高。

图6 模型精度比较
最后,将GCGRU 模型与不具备空间信息捕捉能力的GRU模型进行了对比,结果如图7和图8所示。对于15,30,45 和60 min 的预测时间步长,GCGRU 模型的SRMSE比GRU 模型分别降低了28.9%,21.4%,29.8%和29.8%,SACC分别提高了8.1%,6.3%,10.9% 和10.6%。因此,GRU 和GCN 融合模型实现了数据中时空关系的高效挖掘,预测效果比既有的GRU模型好。

表2 GCGRU模型和基线模型预测性能的比较结果
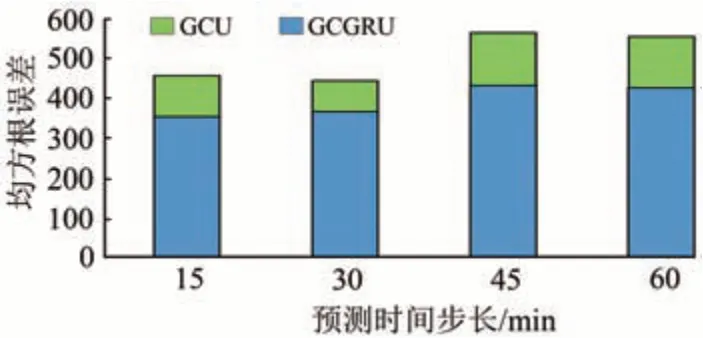
图7 GCGRU模型与GRU模型的均方根误差比较

图8 GCGRU模型与GRU模型的预测精度比较
综上,与所有基线模型相比,本文提出的GCGRU模型在不同的评价指标和预测时间步长情况下的表现性能都最好。
3.4.2 单个车站预测性能
将GCGRU 模型与GRU 模型在每个车站的预测性能进行了进一步的比较分析,得到图9和图10。由图可知,对于每个车站而言,GCGRU 模型的SRMSE比GRU 模型的都低,R2GRU 模型的也高;特别在公园前车站,GCGRU 模型与GRU 模型的SRMSE差距最大,前者相对于后者降低了47.8%;在体育西路车站,GCGRU 模型与GRU 模型的R2差距最大,前者相对于后者提升了23.9%。此外,GCGRU 模型预测结果中琶洲站的SRMSE最高,R2最低。这主要是因为琶洲车站附近有展览中心,经常会有展览活动,因此预测效果不是很好,未来需要进一步挖掘时空关系和外在因素。

图9 GCGRU模型和GRU模型在不同车站的均方根误差比较

图10 GCGRU模型和GRU模型不同车站决定系数比较
图11为6 个车站的2017年5月客流拟合图。由图可知:琶洲站和珠江新城站的客流呈单峰趋势,且都为早高峰;其余车站都呈现早晚双峰趋势。进一步分析,在琶洲站,GRU 模型在高峰时期的预测值比真实值低,如图11(c)所示;而在杨箕站,GRU 模型在高峰时期的预测值又比真实值高,如图11(e)所示。因此,GCGRU 模型的预测效果优于GRU模型。


图11 不同车站的客流拟合曲线图
3.4.3 邻接矩阵影响
为了验证旅行时间邻接矩阵的有效性,将GC⁃GRU 模型与地理邻接矩阵的模型进行了比较。令基于地理邻接矩阵的模型为GCGRU*,比较GC⁃GRU 与GCGRU*在不同预测步长下的SRMSE与SACC,如图12所示。针对15,30,45 和60 min 的预测步长,GCGRU 比GCGRU*的SRMSE分别减少了6.1%,2.7%,2.4%和5.3%;SACC分别增加了0.8%,1.0%,1.0% 和3.0%。由此可见,GCGRU 的预测性能更好,因此基于旅行时间构建的邻接矩阵更适合于城市轨道交通网络的短期客流预测。
4 结 语

图12 GCGRU与GCGRU*预测的均方根误差和精度比较
本文提出了1 种新的融合循环门控单元的时空图卷积神经网络模型(GCGRU)来预测城市轨道交通短时客流。循环门控单元用以提取时间特征,图卷积神经网络用以提取空间特征。以广州地铁路网6 个车站的短时客流预测为例进行模型的有效性验证。结果表明,该模型的预测性能优于ARI⁃MA,SVR,BP 和GRU 等基线模型,对于整体预测结果来说,精度至少提高了6.3%,最多可提高80.5%。对于单站客流预测结果来说,精度至少提高了1.4%,最多可提高23.9%。因此,本文提出的模型能够有效地刻画各车站客流间的时空演化关系,具有精度高、解释性强等特点,可以较好地为城市轨道交通日常客流组织和管理提供辅助决策。
本文提出的模型是1 个静态的空间卷积网络模型,其邻接矩阵不会随着时间而改变。但实际上,各站点之间的空间关系会随时间变化。因此未来可尝试将动态的GCN与GRU相结合来预测客流。本文提出的模型目前只考虑了邻接矩阵和进站客流对出站客流的影响。实际上,出站客流还受到周期、时段以及天气等因素的影响,未来可将这些因素考虑到模型中,以提高模型精度。此外,未来本模型还可以考虑应用在进站量预测上。
