考虑颗粒破碎的高铁路基粗粒土填料循环压密本构模型
2020-08-06叶阳升蔡德钩闫宏业尧俊凯
叶阳升,蔡德钩,耿 琳,闫宏业,尧俊凯,陈 锋
(1.中国铁道科学研究院集团有限公司,北京 100081;2.中国铁道科学研究院集团有限公司 高速铁路轨道技术国家重点实验室,北京 100081;3.北京铁科特种工程技术有限公司,北京 100081)
近几年,中国的高速铁路工程建设迎来了蓬勃发展。截至2019年底,我国运行高速铁路里程已达3.5 万km,占全球高速铁路长度的60%以上,位居世界第一。按照《中长期铁路网规划(2018年中期调整)》,今后我国仍将持续一定规模的高速铁路建设,但中国高速铁路发展已经从大规模建造进入长期安全稳定运营阶段,铁路路基结构层稳定与否是高速铁路安全、舒适运行的重要保障[1]。
图1为我国高速铁路无砟轨道路基结构典型剖面图,主要分为基床表层、基床底层和基床以下的路堤本体部分[2-3]。一般基床表层由级配碎石填筑,工程特性良好。而基床底层则由A,B 组填料填筑,且底层厚度为2.3 m,一般占路基总高度的一半以上,因此是引起路基结构变形的重要因素。为了能够对此部分路基结构在列车荷载作用下的变形特征进行定量描述,并对未来几十年路基运营状况进行安全评价,建立数值计算模型是必要手段,而选择合适的动本构模型又是数值模拟结果准确且可靠的重要保障。
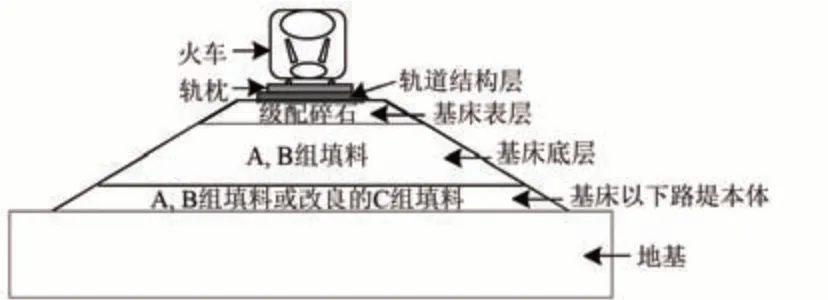
图1 中国高速铁路无砟轨道路基结构典型剖面图
在室内试验方面,随着大型室内动力三轴试验设备的快速发展,针对循环荷载作用下粗颗粒高铁路基填料的动力学特性,许多学者开展了大量的研究工作[4-12]。这些研究全面测试描述了与基床填料状态有关的物理和力学参数,研究了不同动应力幅值、不同围压、不同含水率对粗粒土土样累积变形的影响,揭示了累积变形随循环荷载振动次数的演化规律,建立了累积变形与循环振动次数、动应力幅值、围压等因素之间关系的经验表达式。但是这些基于试验结果建立的经验模型仅能捕捉每次循环荷载作用下产生的累积变形,无法模拟实际动力作用过程中的循环加卸载过程。
在本构模型方面,迄今为止,已经发展了多种土的动力本构模型。黏弹性模型的典型代表等效线性化模型最早由Seed 在1968年提出,该模型通过等价线性化的方法近似考虑土的动力非线性性能[13]。Hardin-Drnevich 模型[14]、Ramberg-Osgood模型[15]、双线性模型及一些组合曲线模型均属于不同形式的等效线性化模型。Mroz 于1967年首先提出了塑性模量场理论,代表着土体动力弹塑性模型研究的正式开始[16]。Iwan,Provest,Zienkie⁃wicz 和Yang,Elgamal 等也分别建立了各具特色的多屈服面模型[17-20]。在国内,王建华、徐干成、陈生水和庄海洋等均建立了各自的多屈服面模型[21-24]。继而,Dafalias[25]以剑桥模型为基础提出了更为简化的边界面模型。Tabbaa[26]将修正的剑桥模型推广为能够描述黏土在循环荷载作用下滞回反应特性的双面动力硬化模型。但是,上述提及的动本构模型普遍存在2 个方面的问题:其一,只能模拟循环荷载次数较小的情况(如地震荷载);其二,并没有考虑循环荷载作用下的颗粒破碎效应。
本文在文献[27]本构理论的基础上,基于临界状态土力学理论和经典塑性力学原理,结合循环荷载三轴试验,进行考虑颗粒破碎的高铁路基粗粒土填料循环压密本构模型研究。
1 高铁路基粗粒土填料变形特性
1.1 压密性
循环荷载作用下高铁路基粗粒土填料一般表现为非线性、应力依赖性等特征。甚至是应力水平与静强度十分接近的情况下,粗粒土填料依然表现出很强的压密特性[27-28]。在初始加载条件下,轴向应变迅速发展,并在卸载过程中部分回弹,而后的每次循环荷载都会产生持续的塑性应变增量。但是,塑性应变增量的幅值会随着振动荷载次数的增加而逐渐降低。这是因为,在循环荷载的作用下,由于应力历史的作用,导致粗粒土填料的刚度越来越大,进而在后续的荷载作用下,累积应变减小。在循环荷载作用下,高铁路基粗粒填料累积变形的发展是1 个逐渐发展的过程,其中每个单一荷载会产生1 个很小的应变增量。大量的动三轴试验表明,初始加载条件下产生的应变较大,但在应力幅值和围压不变的前提下,后续应变增量会不断减小。这就是粗颗粒填料在循环荷载作用下的压密特性,深刻理解和揭示这一特性,有助于指导建设期压路机振动荷载和运行期高速列车荷载对粗颗粒路基填料压实和振动效果影响的研究。
1.2 破碎性
在静动力荷载的作用下,高铁粗颗粒路基填料会产生不同程度的颗粒破碎。Hardin[29]提出用相对颗粒破碎率Rr描述循环荷载作用下粗粒土填料的破碎效应,即

式中:SMPQ为总颗粒破碎程度,用图2所示的加载前后高铁路基粗粒土填料级配曲线中初始级配曲线、加载后级配曲线和颗粒粒径等于0.075 mm 的直线围成的面积表示;SMPN为潜在颗粒破碎程度,用图2中初始级配曲线、100%直线和颗粒粒径等于0.075 mm的直线围城的面积表示。
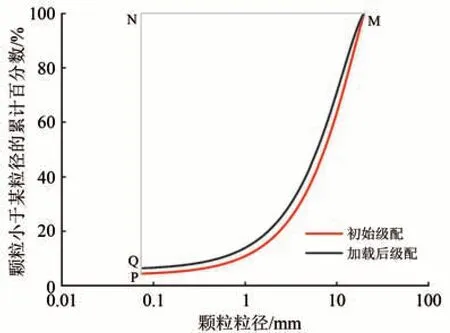
图2 加载前后高铁路基粗粒土填料级配曲线
2 高铁路基粗粒土填料循环压密模型的建立
2.1 模型假设
应力控制条件下的循环三轴荷载引起的高铁路基粗粒土填料应力路径如图3所示。首先,试样受到围压作用,等向固结到初始平均应力σp,0,继而在初始应力的作用下达到最大平均应力σp,max(点B),而后卸载至最小平均应力σp,min(点A),后继加卸载事件在点A和B之间,沿着路径AB进行。
为了简单方便地建立循环荷载作用下粗粒土填料动本构模型,提出了如下2点假设。
(1)在初始加载条件下,粗粒土填料产生弹塑性变形。将初始加载条件达到的最大应力状态作为当前加载条件下的最大加载面。
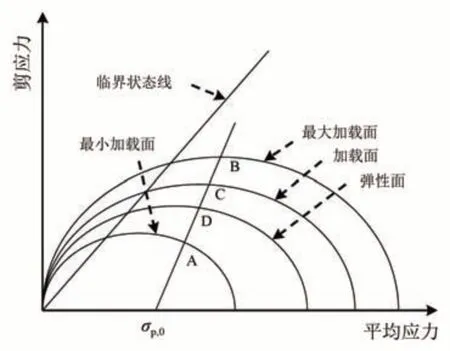
图3 3轴应力状态下粗颗粒路基填料理想化应力路径
(2)存在1 个随着振动次数而不断变化的弹性面。弹性面外部的变形为塑性变形,而弹性面内部则认为是弹性变形。
2.2 考虑颗粒破碎的剪胀方程
在3 轴应力条件下,基于能量守恒原理,可以得到应力、应变和颗粒破碎的如下关系[27]。

式中:σq和σp分别为偏应力和平均应力;dεv和dε1分别为轴向应变和体应变增量;φf为基本摩擦角;EB为每单位体积颗粒破碎所消耗的能量。
根据文献[30]的研究,EB可用单位体积塑性功Wp表示,而Rr与Wp存在双曲线关系,即

式中:a和b为经验参数。
针对循环荷载作用下高铁路基粗粒土填料的室内三轴试验,Wp可由滞回曲线围成的面积计算得到,进而由式(3)便可求得在循环荷载作用下的Rr。然后,将Wp和Rr与累积变形一一对应,最终可分别得到相对颗粒破碎率和单位体积塑性功消耗率可用线性关系表示[27]为

式中:β为经验参数。
据此,再结合应力不变量和应变不变量的表达形式,式(2)可以改写为

式中:dεs,p和dεv,p分别为塑性体应变和剪应变增量;ηM为临界状态应力比;ηi为当前应力比。
在实际工程中,高铁路基粗粒土填料受到诸多因素影响,采用对材料性能影响较为显著的循环应力比ηc和振动次数N作为影响因素,考虑其对颗粒破碎率的影响,为了描述不同工况下的振动荷载加、卸载幅值,引入乘子ln进而建立颗粒破碎率随应变发展的演化规律函数,即

式中:fSR和fN分别为循环应力比和循环振次对颗粒破碎率的影响修正函数。
在σq—σp应力空间内,根据轴对称应力条件下剪应变εs,p与轴向应变ε1和径向应变ε3的关系式并取泊松比等于0.3,可以得到ε1=1.15εs,p,联合式(6),代入式(5),得到
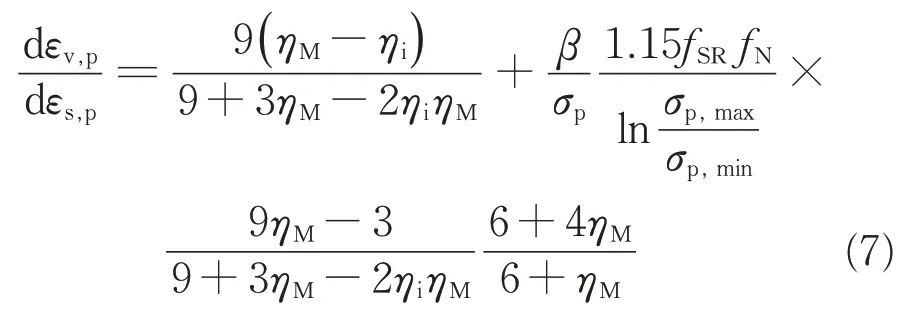
考虑到式(7)中一些为常数的参数,为后续表述方便,将式(7)改写为
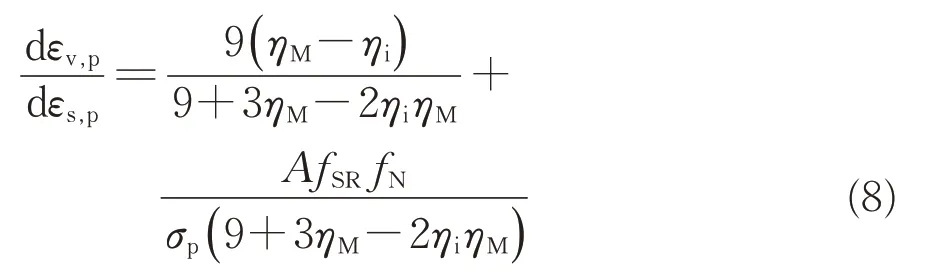
其中,

式(8)即为考虑颗粒破碎效应的粗粒土填料在循环荷载作用下的剪胀方程。
2.3 本构方程的增量表达形式
为了能够准确描述累积变形特性,同时也为了数值编程的方便,经典弹塑性理论常将总应变向量ε分解为

式中:εe和εp分别为弹性应变向量和塑性应变向量。
上式的增量形式可写为

式中:dε,dεe和dεp分别为总应变增量向量、弹性应变增量向量和塑性应变增量向量。
类似地,对于σq—σp应力空间内对应的应变不变量,剪应变增量dεs和体应变增量dεv可写为

式中:dεs,e,dεs,p,dεv,e和dεv,p分别为弹性剪应变增量,塑性剪应变增量,弹性体应变增量和塑性体应变增量。
在弹性范围内,dεs,e和dεv,e可分别采取下式进行计算。

式中:ei为剪切开始时刻的初始孔隙比;G为剪切模量;κ为等向压缩回弹试验回弹曲线的斜率。
塑性阶段的应变向量可由下式获得[27]。

式中:fh,fg和ff分别为硬化函数、塑性势函数和屈服函数。
2.4 塑性势函数
在σq—σp应力空间内,塑性应变增量的方向与塑性势面是垂直的,因此有

将式(16)代入式(8)可得
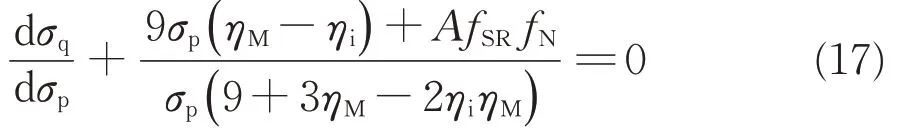
不难看出的是,式(17)的解即为塑性势函数。但是由式(15)可知,并不需要精确的塑性势函数,而仅需得到塑性势函数分别对σq和σp的偏微分形式即可,参考文献[27]给出的简化计算方法,可以得到塑性势函数对偏应力σq和平均应力σp的偏导数分别为


2.5 屈服函数
本文模型仅考虑剪应力引起高铁路基粗粒土填料的塑性变形,而忽略静水压力对填料塑性变形的影响。在σq—σp应力空间内,屈服函数ff可表示为

当循环荷载加载路径与屈服函数重合时,即屈服函数等于0 时,材料进入屈服,表现为塑性变形的特性。
2.6 初始加载条件下塑性应变计算
利用式(15)—式(20),并结合Indraratna和Salim 提出的由不排水应力条件推导硬化函数的方法[31],可以得到初始加载条件下的塑性应变为
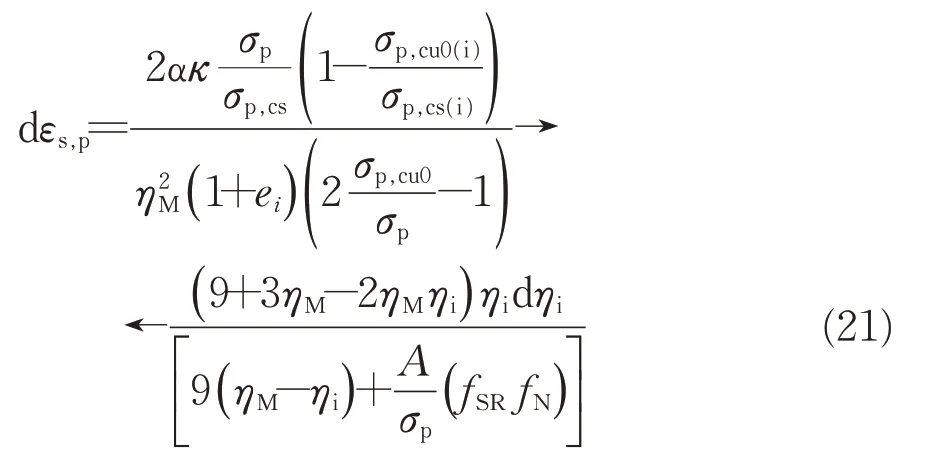
式中:α为与粗颗粒路基填料初始刚度有关的参数;σp,cu0和σp,cs分别为当前应力状态下不排水应力路径起点和临界状态线交点的应力;σp,cu0(i)和σp,cs(i)分别为开始加载时刻应力状态时σp,cu0和σp,cs的初值。
由于在低围压条件下,当前应力比有可能会趋近于临界状态应力比,如此会导致一个较大的剪应变增量值,因此文献[27]的建议,用η*i=替代ηi,使得数值计算过程中应力比的取值能够大于临界应力比,进而保证数值计算的稳定性和鲁棒性。根据文献[27]可知,式(21)和式(8)可以分别改写为


2.7 后继加载条件下塑性应变计算
如本文所述,在循环荷载作用下,高铁路基粗粒土填料初次加载产生的应变最大,而后随着振动次数的增加,累积变形逐渐趋于稳定,即表现出了压密性。从本构方程的数学表达的角度出发,可以采取修正代表材料刚度的参数来模拟路基填料的压密性。因此,对初始加载条件下的塑性应变计算公式进行刚度修正,从而得到新的后继加载条件下塑性剪切应变增量计算式
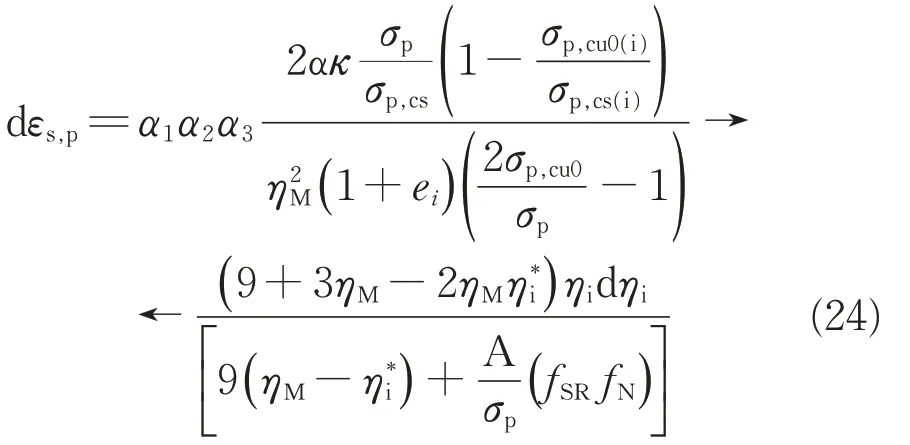
其中,
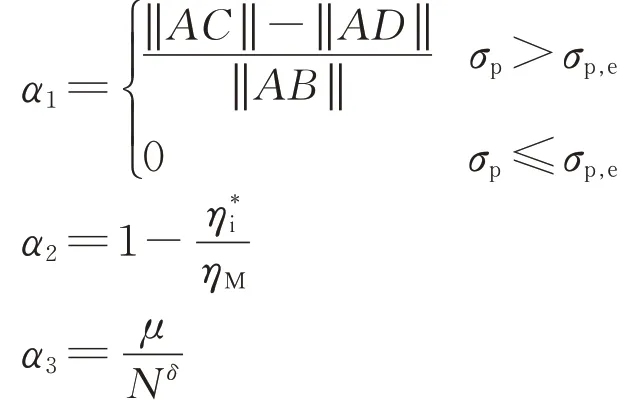
式中:α1为考虑随动硬化效应的参数;α2为考虑后继加载应力比影响的参数;α3为考虑振次影响的参数;μ和δ为与循环振次有关的模型经验常数;‖AB‖,‖AC‖和‖AD‖为σq-σp应力空间内两点之间的距离(见图3);σp,e为弹性平均应力(对应图3中的点D)。
α1的引入是为了准确模拟包辛格效应。由于在一定的振动次数之后,材料表现为弹性,因此引入弹性面来描述加载历史的影响。弹性面随着振次的增加而不断硬化。σp,e则在给定的应力路径AB之间变化,前人给出的σp,e与振次N之间的关系[27]为
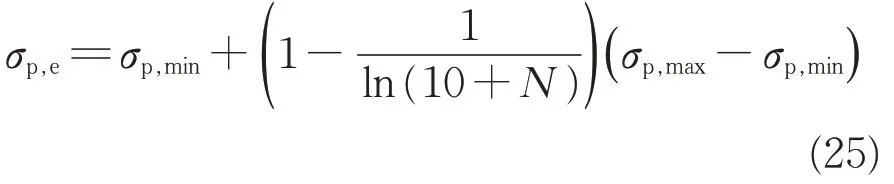
图3中,点D 是用来控制材料在后继加载条件下变形的,点C 代表当前应力位置。如果C 高于D,则材料表现为弹塑性,反之,则为弹性。
α2的引入是为了模拟应力比大小的影响。当填料受到较大应力作用时,即应力比越接近临界状态应力比,则填料的刚度越大,从而产生的变形则越小。
α3的引入是为了模拟循环振次的影响,它是1个与振次N有关的函数,随着加载次数的增加,参数α3逐渐增大,进而反应填料的刚度增加,累积变形减小。
通过上述公式计算得到剪应变之后,便可由式(24)计算得到塑性体应变增量。最终,总的剪应变和体应变增量可由式(11)和式(12)计算得到。
3 高铁路基粗粒土填料循环压密模型在ABAQUS程序中的实现
3.1 循环压密模型的数值实现流程
有限元软件ABAQUS 应用范围广、功能强大,可以模拟由简单线性到复杂非线性的各种问题,当中不仅提供了标准的有限元分析程序,还具有良好的开放性能。用户可以借助二次开发的平台,开发用户子程序接口和应用程序接口,以此扩展主程序的功能,在实际工程中得到广泛应用[32]。本文基于有限元软件ABAQUS 二次开发接口,选用FORTRAN 语言编写高铁路基粗粒土填料循环压密模型的UMAT 子程序。UMAT 子程序主要流程如图4所示。
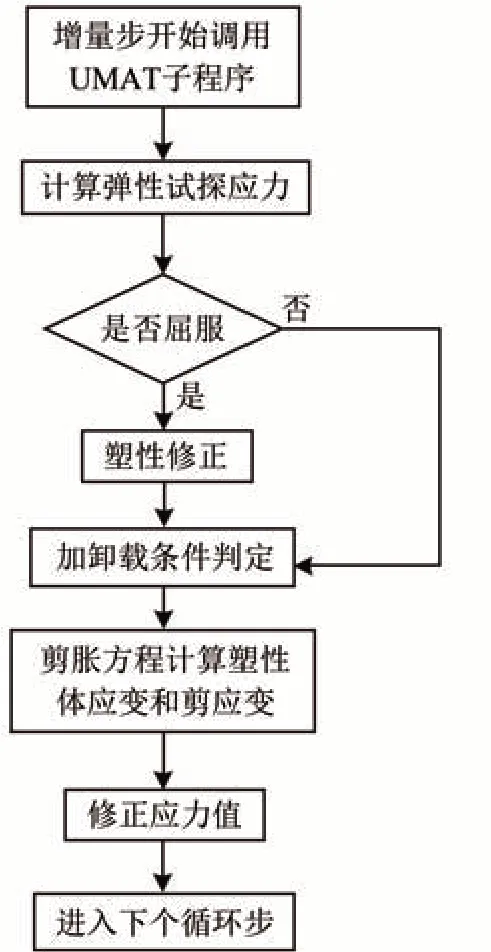
图4 循环压密模型数值实现流程
3.2 循环压密模型的数值实现和验证
基于上述对循环压密模型和有限元数值实现方法的描述,本节采用二维对称的方法,并编制有限元子程序,预测粗颗粒路基填料三轴测试结果。
图5为循环三轴试验的数值模拟示意图。为了方便,取圆柱形三轴试样的二维平面进行模拟,即图5(a)中三轴试样的阴影部分,采用ABAQUS中二维8节点对二次减缩积分单元;图5(b)显示了ABAQUS 模型的网格划分及边界条件。模型左边界为中心轴,不能发生侧向变形,而模型的下边界约束竖向和径向变形。模型顶部径向被固定,但竖向可以自由变形。采用2 个分析步模拟循环加载三轴试验过程:第1步,给定模型边界和围压;第2步:对模型施加竖向循环荷载。

图5 循环三轴试验数值模型
本文针对文献[33]和文献[34]中的循环荷载作用下粗粒土三轴试验进行数值计算。数值计算中,模型参数取值的方法如下。
根据室内振动压实试验结果,绘制相对颗粒破碎率与单位体积塑性功关系曲线,如图6所示。采用式(3)对试验结果进行拟合,可以得到高铁路基粗粒土填料的经验参数a和b分别等于1 855 和0.083。

图6 相对颗粒破碎率与单位体积塑性功关系
由循环荷载下三轴试验得到的应力—应变曲线围成的滞回圈面积计算Wp,由上述确定的参数a和b计算循环荷载作用下的Rr。然后,将Wp和Rr与累积变形一一对应,最终分别得到相对颗粒破碎率和单位体积能量消耗率如图7所示。由图7可见,二者呈线性关系,拟合得到经验参数β等于1 855。
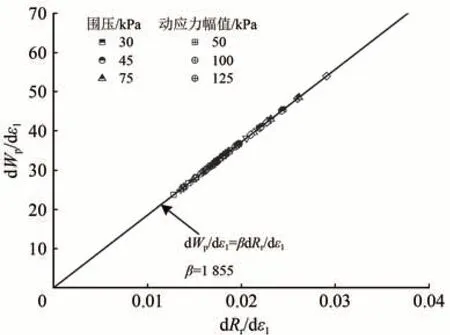
图7 相对颗粒破碎率与单位体积能量消耗率关系
由文献[34]的三轴试验结果,可以得到fSR与循环应力比以及fN与循环振次的关系如图8所示。基于最小二乘法原理,拟合得到fSR和fN的经验表达式为
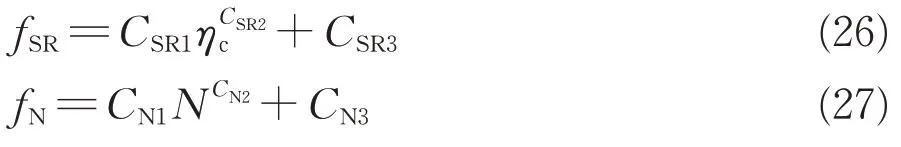
式中:σd为三轴试验竖向动应力幅值;σ3为三轴试验围压;CSR1,CSR2,CSR3,CN1,CN2和CN3为拟合参数。
表1给出了相对颗粒破碎率的修正函数式(26)和式(27)的拟合系数具体取值。
在循环荷载作用下高铁路基粗粒土填料三轴试验的模拟中涉及的其他参数可根据尝试试错法获得,具体取值见表2。

图8 相对颗粒破碎率修正函数
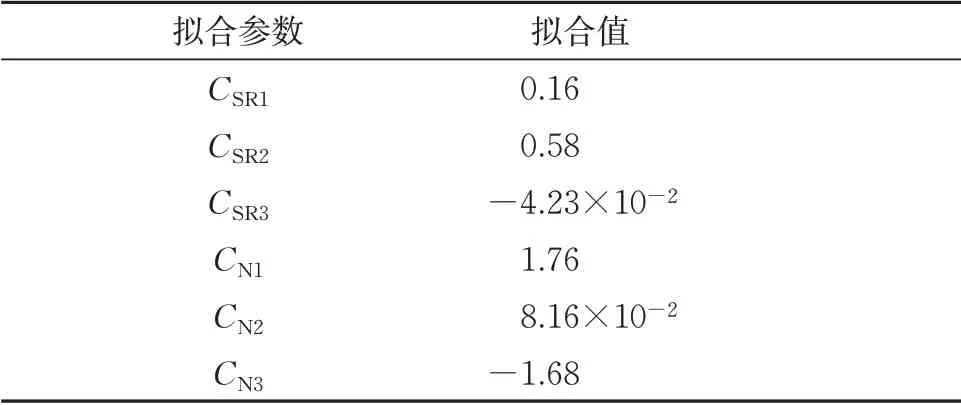
表1 颗粒破碎率修正函数参数取值

表2 数值实现中循环压密模型参数
图9给出了循环荷载作用下高铁路基粗粒土填料累积变形试验结果和数值计算结果,由图9可见,本文提出的循环压密模型计算结果可以较准确地预测不同围压和应力幅值作用下的累积变形,同时也准确预测了随着累积振次的不断增加,累积应变不断趋于稳定的循环压密特性。这充分说明了本文提出的循环压密模型理论公式以及有限元计算实现方法是准确且合理的。
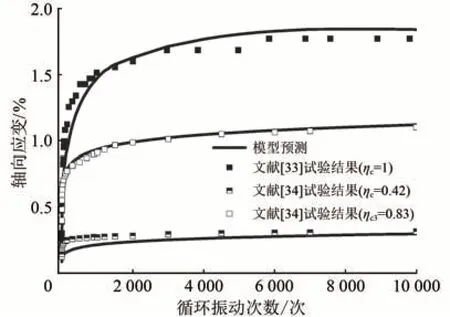
图9 高铁路基粗粒土填料累积轴向变形试验结果和数值结果
4 结 论
(1)基于高铁路基长期反复低幅循环荷载的受力特性,针对高铁路基粗粒土填料,依据临界状态土力学理论,给出了填料颗粒破碎与塑性功经验表达式,修正并提出可以考虑颗粒破碎与应力比影响的粗粒土填料剪胀方程。
(2)依托经典弹塑性理论,引入应力比与循环振动次数修正函数,通过弹塑性解耦,推导出基于修正剪胀方程的路基粗粒土填料循环压密本构模型。
(3)建立所提模型的“弹性预测-塑性修正”数值分析求解程序,采用FORTRRAN 语言编写计算程序,借助有限元软件ABAQUS 所提供的二次开发程序接口,实现本构模型的程序化计算。
(4)与前人所做循环荷载作用下高铁路基粗粒土三轴试验对比,表明本文提出的考虑颗粒破碎的循环压密模型能够较准确地模拟填料长期累积变形和循环压密特性。
