侧风下高铁列车交会运行时车—桥耦合振动

2020-08-06郭文华洪新民陈春霞

中国铁道科学 2020年4期

郭文华，洪新民，陈春霞

(1.中南大学土木工程学院，湖南长沙 410075；2.浙江省交通规划设计研究院有限公司公路设计研究院，浙江杭州 310006）

随着我国高速铁路网的建设采取了用桥梁代替传统路基的办法，不但保证了高速列车运行的高安全性、高平稳性和乘车舒适性的要求，而且避免了滥占更多农业耕地，因此我国高速铁路呈现出线路中桥梁占比高的特点，部分线路桥梁占比甚至超过了90%［1］，列车在桥上发生交会的概率也随之显著增加。由于空气的黏性，高速列车受到的气动力在列车交会过程中发生急剧的变化［2-3］，气动力的急剧变化会增大列车的振动。列车在运行过程中受到强侧风的作用，可能发生脱轨、甚至侧翻的事故［4-5］。在强侧风和列车交会气动力的共同作用下，将会大大降低旅客的乘车舒适性，增大列车发生脱轨、倾覆的可能性。

国内外学者通过数值模拟、风洞试验，实车试验等方法对列车交会时的气动力和高速列车在侧风下的运行安全性等问题开展了研究。李永乐等［6］等通过数值模拟的方法研究了侧风下列车在桥上交会时列车的气动力特性。邱晓为等［7］通过风洞试验模拟了单线列车运动与静止列车的交会，分析了车速、风速、合成风向角、等参数对车辆交会气动力系数的影响。翟建平等［8］利用动网格技术，数值模拟分析了桥梁高度对列车交会过程中的行车安全性的影响。陈厚嫦等［9］通过现场测试了高速列车在隧道内交会运行时的气动力作用。田红旗等［10］，熊小慧等［11］通过实测CRH2型列车以250 km·h-1等速交会时空气压力波数据，得到了4.4 m的线间距不会影响列车运行安全性的结论。郭向荣等［12］，夏禾等［13］等采用时域分析法，分析了脉动风作用下列车单线行车通过大跨度斜拉桥时的车—桥耦合动力响应，评价了列车的运行安全性，并提出了不同风速下对应的列车车速的限值。

在上述研究中仅考虑了列车交会对列车气动力的影响，或仅考虑了侧风对单线行车的安全性的影响，忽略了列车交会气动力对列车运行安全性的影响。在目前的风洞试验中尚无法实现2 个列车在运动中的交会以及获得列车的交会气动力，一般是根据列车不同相对位置的气动力系数计算列车交会过程的气动力，忽略了列车运动对周围流场改变的影响。

本文借助流体力学计算软件FLUENT 和动网格技术模拟计算2 组3 节列车在交会过程中受到的气动力，将计算得到的气动力时程通过自编程序扩展至2 组8 节列车交会的气动力时程，将列车和桥梁的气动力时程施加到由SIMPACK 软件和AN⁃SYS 软件联合建立的风—高速列车—多跨简支梁三维动力分析模型中，研究侧风下列车在多跨简支梁桥上交会运行时的动力响应，并根据列车运行的安全性指标提出在侧风下考虑列车交会气动力的列车安全运行的速度阈值。

1 列车和桥梁的气动力

1.1 列车气动力六分力

在自然风场中，作用于高速列车的气动力如图1所示，包括：侧力Fx、阻力Fy、升力Fz、俯仰力矩Mx、侧倾力矩My和侧偏力矩Mz。

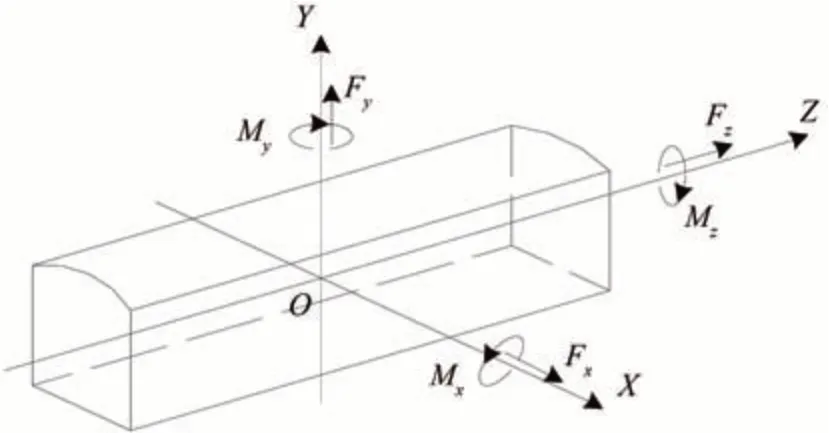
图1 列车气动力六分力示意图

1.2 桥梁气动力三分力

自然风流过桥梁时，桥梁受到空气动力形成的气动作用［14］，包括气动阻力Fd、升力Fl和力矩Fm，如图2所示。

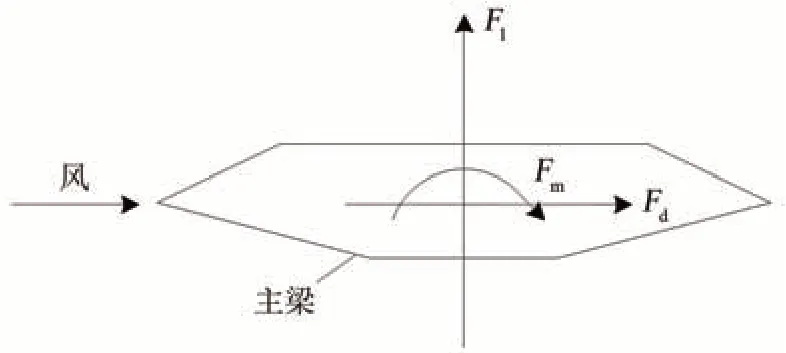
图2 桥梁气动力三分力示意图

1.3 列车交会气动力计算模型

以FLUENT 软件为计算平台，采用动网格技术建立2 列列车在桥上交会的1∶1 全尺寸三维模型，计算侧风下列车在桥上交会过程中受到的气动力。将列车在桥上交会过程中的流场视为黏性不可压缩非常定流场，并采用RANS 方法研究由列车高速运动引起的湍流运动。考虑到计算机的计算能力以及中间车的气动力特性的相似性，采用头车、中间车、尾车3 节车厢编组的列车进行数值模拟，每节车长25.25 m，宽3.27 m，高3.82 m。桥梁采用我国高速铁路常见的32 m 双线简支梁，共7跨。在保证计算精度和速度的同时，忽略列车的车窗、受电弓和桥梁护栏、轨道的影响。计算区域与整体坐标系如图3所示，计算区域的长、宽和高分别为300，240 和60 m，采用非结构化的四面体网格对流场进行划分。网格采用放射性网格，靠近列车与桥梁的网格足够小，远离这些构件的区域适当地放大，从而满足计算精度并兼顾计算工作量，整个区域网格最小单元尺寸为0.2 m，网格总量约399.45 万个。列车的运动通过编辑UDF 程序来实现。列车运动引起网格变形，当网格质量低于某个特定值时，通过使用局部网格重构（Local Remeshing Method）和光滑（Smoothing Method）动网格功能对局部的低质量网格进行更新，以保证列车运动时刻网格的质量和计算结果的精度。初始时，2 列列车头车鼻尖之间的距离为72 m，记为－72 m。分析时列车考虑等速交会且侧风方向垂直列车运行方向。

图3 计算区域及整体网格分布图（单位：m）

1.4 列车交会气动力结果

根据上述列车交会气动力计算模型，计算了在风速为10 m·s-1，湍流度为5%的侧风下列车交会运行时的气动力时程，其中列车头车与中车的气动力结果如图4所示。从图4可知：侧风下当2 列列车在交会之前和交会结束后，列车的气动力主要以侧风作用为主，气动力大小变化很小，而列车在交会的整个过程中，列车气动力会发生多次的突变，此时作用在列车上的气动力包括侧风作用和列车交会引起流场改变对列车作用的气动力，并且由于迎风侧列车的遮风效应，背风侧列车气动力变化值大于迎风侧列车的气动力变化值。

图4 3节编组列车交会时头车和中车气动力时程曲线

以列车头车的侧力说明列车交会过程中的气动力。

（1）当2 列列车头车的即将碰面时，头车前端的气压迅速增大成正压，此时列车将受到向外的推力作用，背风侧头车侧力迅速增大，迎风侧头车列车迅速减小。

（2）随着列车的前进，列车的气动力逐步达到一个峰值点后，列车周围的气压逐步减小，列车受到向外的推力作用逐步减小，背风侧头车侧力逐步减小，而迎风侧头车列车逐步增大。

（3）当列车头车与对面列车中车交会时，作用在列车头车上的气压比较稳定，此时列车头车的气动力也变化很小。

（4）当列车头车与对面列车尾车交会时，由于此时列车之间气压为负压，所以列车将受到向内的推力作用，背风侧头车侧力迅速减小，而迎风侧头车列车迅速增大。

（5）当列车头车与对面列车尾车相互离开时，由于此时列车之间气压逐步增大，所以列车受到向内的推力也逐步减小，背风侧头车侧力逐步增大，而迎风侧头车列车迅速减小。

（6）当2 列列车的尾车完全离开时，列车的气动力逐步恢复到列车交会之前的大小。

根据中间车厢气动力的相似特性，通过自行编写程序将3 节列车交会的列车气动力时程曲线延长至本文计算需要的8 节列车交会的列车气动力时程曲线。图5为列车头车侧力扩展为8 节车厢编组的交会气动力时程曲线。

图5 8节编组列车交会时头车侧力时程曲线

2 风—车—桥耦合系统力学模型

2.1 车辆动力学模型

列车模型采用二系悬挂四轴车辆，由1 个车体、2 个转向架和4 个轮对，共7 个刚体组成。每个刚体有伸缩、横摆、浮沉、侧滚、点头、摇头在内的6 个自由度，单节列车总共42 个自由度，如图6所示。图中：xc，yc，zc，θc，φc和ψc分别为车体在x，y，z，θ，φ和ψ方向的自由度；xt，yt，zt，θt，φt和ψt分别为转向架在x，y，z，θ，φ和ψ方向的自由度；xw，yw，zw，θw，φw和ψw分别为轮对在x，y，z，θ，φ和ψ方向的自由度；2d1和2d2分别为轮对间距和转向架间距；2a1和2b1分别为二系悬挂和一系悬挂的横距；h1，h2和h3分别为车厢质心至二系悬挂顶点、二系悬挂顶点至转向架质心、转向架质心至轮对质心的高度；cx1，cy1，cz1，kx1，ky1和kz1分别为一系悬挂在x，y和z方向的阻尼和刚度；cx2，cy2，cz2，kx2，ky2和kz2分别为二系悬挂在x，y和z方向的阻尼和刚度［15］。

图6 车辆动力学模型示意图

2.2 桥梁、轨道结构动力模型

桥梁、轨道以及桥墩均采用空间梁单元模拟，轨道视为由离散弹性点支撑的Euler 梁。轨道与主梁之间采用扣件连接，以弹簧—阻尼元件的形式考虑。桥墩地基基础的刚度叠加到相应的节点上。桥梁系统的阻尼按照Rayleigh 阻尼考虑，一般对应于低阶频率的阻尼比为2%～5%。桥梁二期恒载作为主梁质量的一部分考虑。

2.3 风—车—桥耦合仿真的实现

车—桥系统耦合振动涉及车辆与桥梁2 个子系统，采用ANSYS 建立桥梁的有限元模型，然后将其导入到SIMPACK 中，与车辆模型和轨道模型共同组成车—桥耦合振动动力分析模型，轨道不平顺作为耦合系统的内部激励，而列车气动力和桥梁气动力作为车—桥耦合系统的外部激励，通过SIMPACK 中的93 号力元作用到车—桥耦合系统上。在轮轨接触面上利用离散的信息点进行位移、速度和力等数据交换，实现风—车—桥的耦合振动仿真分析［16］。在风—车—桥的耦合振动计算中，将车辆和桥梁视为2 个系统，采用不同的算法求解刚体和柔性体的运动方程，列车作为刚体采用后向微分公式求解，而桥梁作为柔性体则采用模态叠加法求解，在时间步长内轮流迭代求解。采用Hertz非线性接触理论计算轮轨法向力，采用简化的kalker蠕变假定计算轮轨切向蠕变力［17］。

3 计算实例

3.1 模型基本参数

以7 跨高速铁路中常采用的32 m 双线简支梁组成多跨简支梁桥为研究对象，线间距为5.0 m。主梁采用箱形截面，材料选用C50混凝土。桥面净宽13.4 m，梁高3.05 m，梁长32.6 m，净跨径31.5 m。桥面二期恒载184 kN·m-1等效为主梁质量进行考虑。桥墩采用空心矩形截面，纵向长度3.3 m，横向长度6.8 m，壁厚0.5 m，墩高16 m，材料为C30混凝土，墩底支承以固结形式考虑，材料的弹性模量E和泊松比μ按现行桥规取值，模型阻尼比为0.02。列车采用德国ICE3 高速列车，车辆参数可参考文献［18］，列车编组为：1 动车+6拖车+1 动车。轨道结构采用双块式无砟轨道，钢轨采用标准60轨，轨道长660 m，轨距1.5 m，设定扣件间距为0.6 m，扣件横向刚度为60 MN·m-1，竖向刚度为120 MN·m-1，横向阻尼为0.12 MN·s·m-1，竖向阻尼为0.15 MN·s·m-1。轨道不平顺根据我国《高速实验列车技术条件》中建议，采用德国轨道低干扰谱进行模拟，空间步长采用0.2 m。

3.2 无侧风环境中列车交会气动力对列车动力响应的影响

为分析无侧风下列车交会气动力对车—桥耦合系统动力响应的影响，在无侧风的环境中分别计算列车在有交会和无交会2 种不同情况下列车以350 km·h-1的速度通过桥梁时的振动响应，其中列车头车的动力响应如图7所示。

由图7可知：①在无侧风环境中列车的动力响应主要是由轨道不平顺导致的，振动响应与轨道不平顺紧密相关；②在有、无列车交会气动力的2种情况下，列车的脱轨系数时程、轮轴横向力、列车竖向加速度时程曲线的变化趋势基本一致，考虑列车交会气动力，列车的轮重减载率有所增大；③列车交会气动力显著增大了列车的横向加速度，列车的横向加速度在3.5 和4.5 s 附近出现显著增大，这是由于列车受到的交会气动力在列车开始交会和交会结束时发生突变导致。

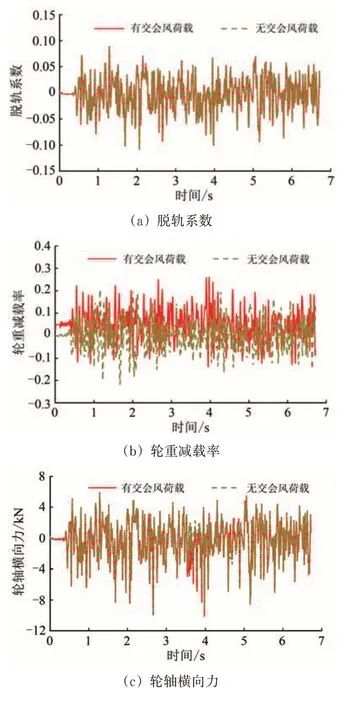
图7 无侧风环境中列车头车动力响应时程

3.3 侧风下列车交会气动力对列车动力响应的影响

为研究侧风下列车交会气动力对车—桥耦合系统振动响应的影响，在10 m·s-1的侧风下，分别计算了考虑列车交会气动力和不考虑列车交会气动力2 种不同情况下列车以350 km·h-1的速度交会通过桥梁时的振动响应，其中列车头车的动力响应如图8所示。

对比图7和图8可知：侧风显著增大了列车的脱轨系数、轮重减载率以及轮轴横向力，侧风对列车横向加速度和竖向加速度的作用比较小；侧风下列车交会气动力对增大列车的横向加速度作用显著，同时会些许增大列车的轮重减载率。

3.4 侧风下列车交会运行的车速阈值

为了保证列车在侧风中运行的安全性，高速铁路管理部门针对不同侧风下列车的运行设置1个车速阈值。计算不同速度的侧风下列车以不同速度在桥上交会运行时列车的动力响应，其中侧风的风速在0～25 m·s-1中以5 m·s-1的梯度递增，车速在200～350 km·h-1范围内以25 km·h-1的梯度变化，共计42 个工况。其中在20 m·s-1侧风下，列车以300 km·h-1速度交会运行时的列车动力响应如图9所示。由图9可知：列车的脱轨系数、轮轴横向力和轮重减载率在列车交会时有增大趋势；列车头车的脱轨系数、轮轴横向力和轮重减载率明显大于中车和尾车相应动力响应的数值。

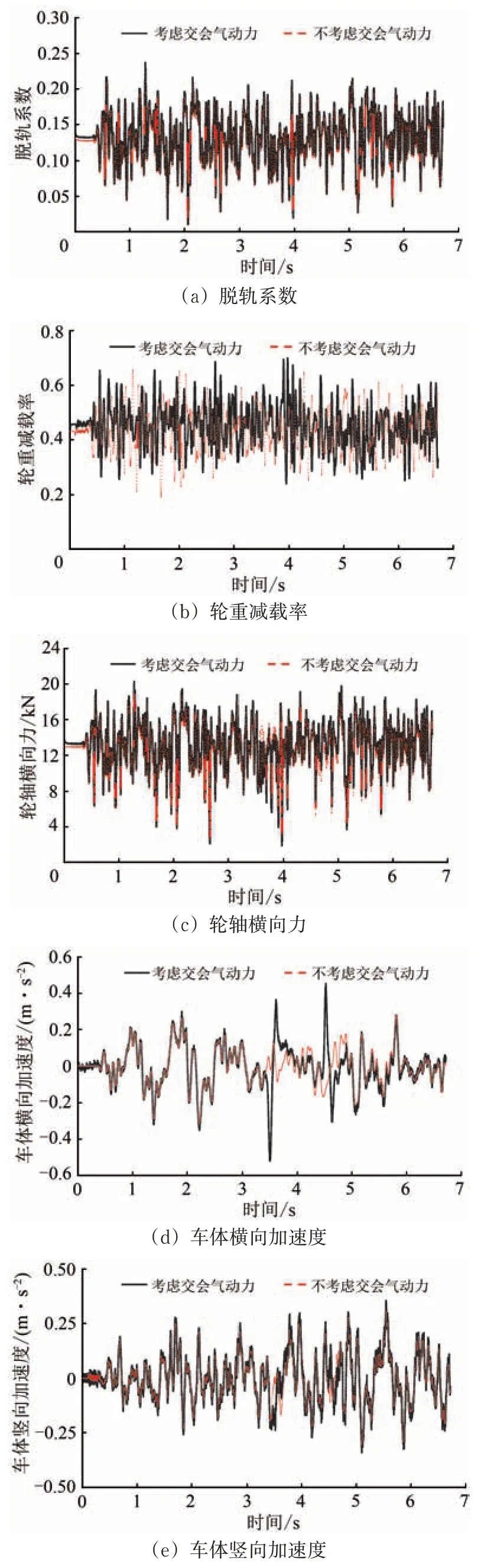
图8 列车头车动力响应时程图

图9 20 m·s-1侧风下列车以300 km·h-1速度交会时的列车动力响应时程

图10绘出了在0～25 m·s-1侧风风速下，列车以200～350 km·h-1车速交会时的列车动力响应。图中虚横线为规范中列车各动力响应的安全限值。由图10可知：列车的脱轨系数、轮轴横向力和轮重减载率均随着风速和车速的增大而增大；各工况下列车脱轨系数和轮轴横向力均满足相关规范要求，而在部分工况中列车的轮重减载率超出规范限值，可见轮重减载率成为控制列车在桥上交会运行安全车速的控制指标。

图10 不同风速下列车动力响应与车速的关系曲线

由图10（b）还可看出：侧风风速小于15 m·s-1、列车以350 km·h-1的车速交会时，列车的最大轮重减载率为0.548，小于相关规范对列车轮重减载率的安全限值0.6，故侧风风速小于15 m·s-1时，列车的车速阈值为350 km·h-1；侧风风速处于［15，20）m·s-1之间、列车以300 km·h-1交会时，列车的最大轮重减载率为0.618；列车以275 km·h-1交会时，列车的最大轮重减载率为0.578，故侧风风速在［15，20）m·s-1时，列车的车速阈值为275 km·h-1；侧风风速处于［20，25）m·s-1之间，列车以225 km·h-1交会时，列车的最大轮重减载率为0.631；列车以200 km·h-1交会时，列车的最大轮重减载率为0.589，故侧风风速在［20，25）m·s-1时，列车的车速阈值为200 km·h-1。