重载铁路钢轨疲劳裂纹萌生影响因素
2020-08-06贾昕昱黎国清刘秀波
贾昕昱,黎国清,刘秀波,杨 飞
(1.中国铁道科学研究院,北京 100081;2.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
滚动接触疲劳裂纹是重载线路上最为常见的一种伤损形式,这种裂纹的萌生和扩展与轮轨之间的接触状态有很大关系。李霞[1]分析了钢轨轨底坡与LM,LMA型2 种车轮的接触状态。Vo K D[2]分析了钢轨存在磨耗时的轮轨接触状态。但是对于轮轨接触状态与裂纹萌生之间关系的研究还相对较少。
有限元方法是分析轮轨接触状态非常有效的一种方法,三维瞬态滚动有限元模型可以得到车轮、钢轨的受力状态以及轮轨接触斑的应力分布等信息。于淼[3]采用三维瞬态有限元模型分析了车辆经过波磨区段时轮轨间的动力响应特性。在对裂纹萌生的分析中,周宇[4]采用多体动力学软件得到轮轨接触斑的应力分布状态,再将接触斑内的力施加到钢轨上,用以对裂纹萌生状态进行分析。但是这些分析过程忽略了车轮滚动过程中接触斑的分布状态是不断变化的。
本文基于临界平面理论建立钢轨疲劳裂纹萌生预测模型,采用三维瞬态滚动有限元模型模拟重载铁路的轮轨接触状态,并分析不同轨底坡和轮轨摩擦系数下轮轨间的接触状态及钢轨裂纹萌生特征,得到不同因素对裂纹萌生的影响。
1 钢轨疲劳裂纹萌生寿命预测模型
对于材料的疲劳裂纹萌生寿命预测,目前大体可分为2 种方法,一种是通过实际测量和模拟试验得到疲劳数据,但是这种方法没有较好的通用性,另一种是疲劳寿命分析法,通过考虑材料的载荷形式以及材料的相应参数分析结构的疲劳寿命,而临界平面法就是这种方法中较为有优势的方法。临界平面法是根据剪应力以及拉应力确定一个物理量,找到这个物理量的最大值所在的平面即临界平面,材料在临界平面上最先产生裂纹。
Jiang 和Sehitoglu[5-6]提出的疲劳参量FP,是基于应变能与临界平面法的一个物理量,为
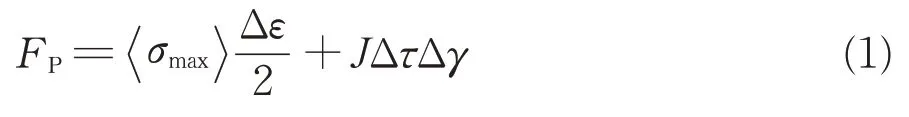
其中,

在有限元分析中,OXYZ为全局坐标系;O′X′Y′Z′为旋转平面上的局部坐标系,并且分别表示钢轨的纵向、横向和垂向,θ为裂纹所在平面的法向向量N与Z′轴间的夹角,ϕ为裂纹所在旋转平面的法向向量在X′Y′平面内的投影N′XY与X′轴的夹角,如图1所示。
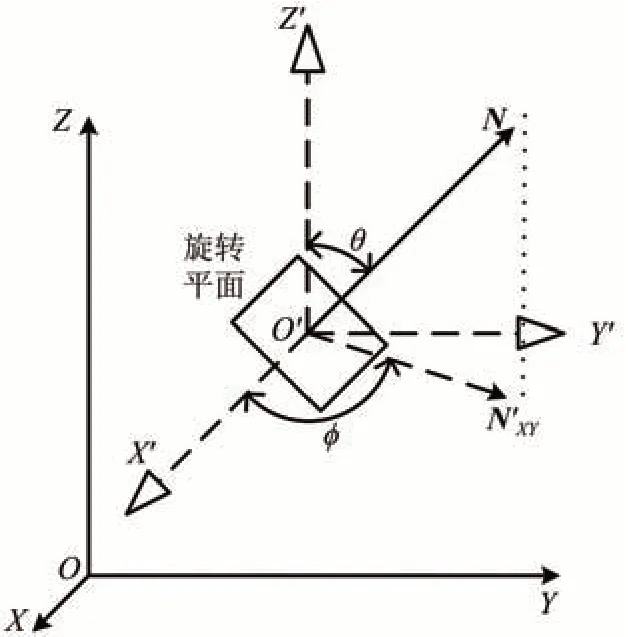
图1 旋转平面示意图
通过有限元分析可以得到所求节点的应力分量σij和应变分量εij,根据张量分析理论可以组成相应的应力矩阵σ和应变矩阵ε。将所得的应力、应变矩阵进行旋转变换,就可得到任意角度平面上的应力分量σ′ij和应变分量ε′ij,分别为
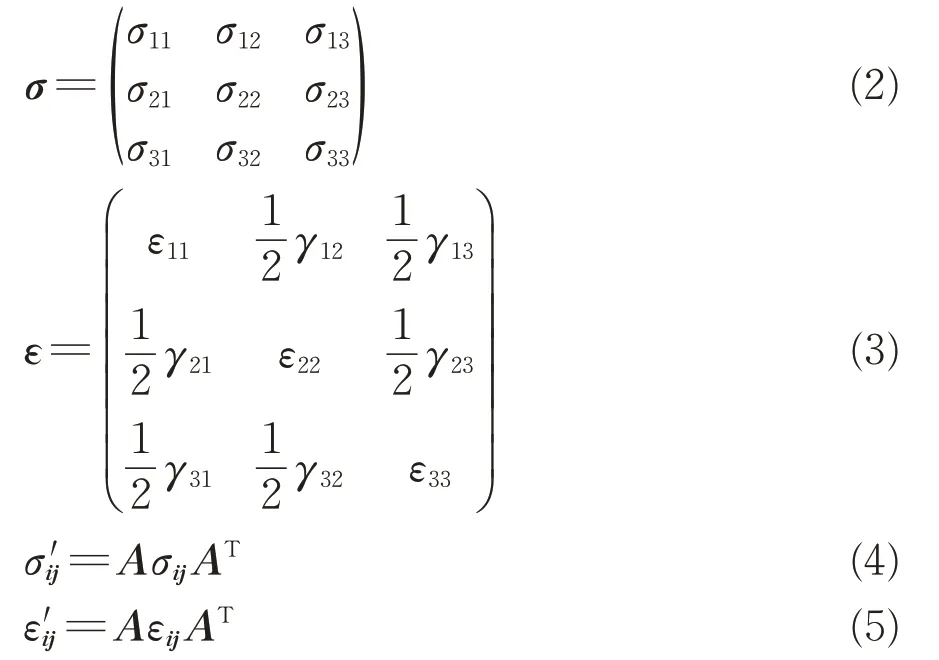
其中,
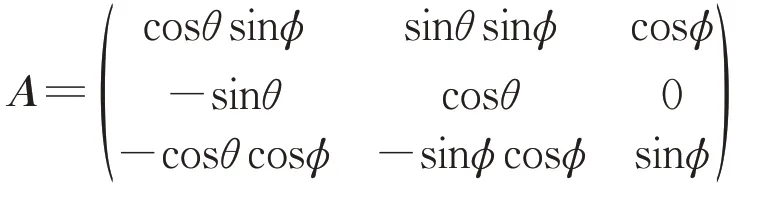
式中:A为张量旋转变换矩阵。
通过对相应单元的疲劳参量进行分析,找到疲劳参量FP的最大值FPmax,其所在平面就是疲劳裂纹萌生的平面,也就是临界平面。这一模型可以将拉应力、剪应力、拉应变、剪应变有机地结合起来,充分考虑到拉应力和剪应力同时对裂纹萌生和扩展的影响。
Akama[7]提出拉伸型裂纹寿命预测模型为
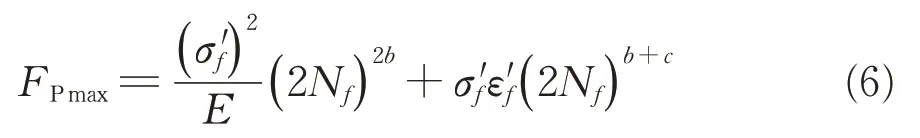
式中:σ′f为拉伸强度系数;E为弹性模量;Nf为轮对的通过次数;ε′f为拉伸延性系数;b为疲劳强度系数;c为疲劳延性系数。
王建西[8]采用剪切型裂纹寿命预测模型,为
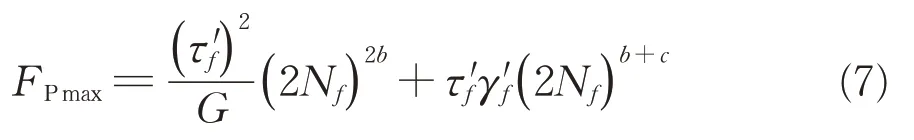
式中:τ′f为剪切强度系数;G为切变模量;γ′f为剪切延性系数。
2 轮轨三维瞬态滚动接触有限元模型
在分析车辆与轨道的相互关系时,传统的多体动力学软件往往倾向于分析结构相对低频的响应,对于高频响应有一定的缺失。而钢轨裂纹的产生和扩展更倾向于轮轨之间的高频作用,传统的多体动力学软件无法较好地解决高频振动问题,因此,采用ANSYS/LS-DYNA 软件建立轮轨三维瞬态滚动接触有限元模型,通过该模型可以分析重载列车与有砟轨道之间的相互关系。由弹簧质量、一系悬挂、轮对、钢轨、扣件、轨枕和道砟组成的有限元模型及轮轨尺寸如图2所示。
由于一系悬挂以上的车辆部分受到高频振动的影响较小,因此车辆一系悬挂以上的部分被简化为1 个刚性质量块,质量块的大小根据列车的轴重来决定。一系悬挂由8 根并列的弹簧阻尼结构组成,用以连接质量块及车轴。由于轮对滚过的距离较短,仿真时忽略滚动过程中轮对横移的影响,但对轮对的横向运动进行约束。车轮及轨道采用真实重载线路中的参数进行模拟,车轮踏面为LM 磨耗型,钢轨为75 kg·m-1的U75V 热处理钢轨。车轮与钢轨之间的接触采用基于罚函数的面—面接触准则,接触面之间的摩擦采用库仑准则。
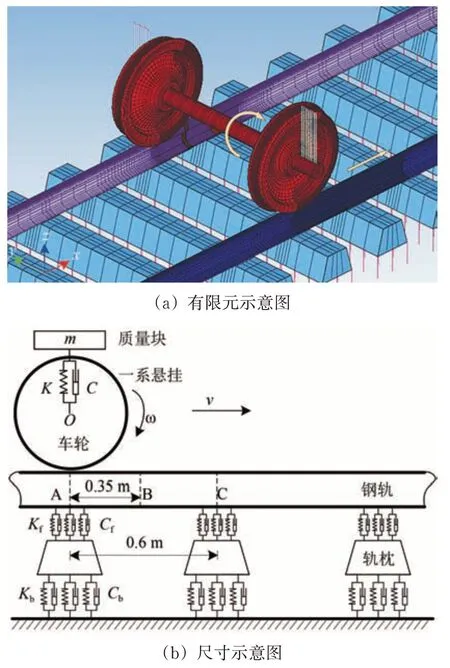
图2 轮轨三维瞬态滚动接触有限元模型
图2(b)中,A 点为轮对滚动的起始点,在该点计算轮轨系统的初始变形。从A点到B点为轮对的动态松弛区,以保证轮对能够平稳地滚动,距离为0.35 m。从B 点到C 点为疲劳裂纹萌生计算区,用以计算钢轨疲劳裂纹的萌生。轨道的总长度为18 m,其间包括30 个轨枕。在动态松弛区以及计算区内钢轨单元划分的较为细密,远离轮对滚动的地方单元划分较为稀疏。为了得到较为精确的轮轨接触状态,在车轮与钢轨可能的接触区域内均划分较为细密的单元,在轮对的起始滚动点即A 点处,钢轨的最小网格尺寸为1 mm,在动态松弛区内最小网格尺寸为2.5 mm,在疲劳裂纹萌生计算区内,最小网格尺寸为0.7 mm。整个模型的总节点数和总单元数分别为1.18×106个和1.04×106个。有限元模型中所用参数见表1[9]。
有限元分析得到车轮滚过平顺钢轨时的轮轨垂向力如图3所示。图中:A 点,B 点和C 点为图2(b)中的位置点。从图3可以看出:从A 点到B 点的范围内,轮轨垂向力的波动幅值较大,没有达到稳定的状态,这就是由于轮对从静态到动态转变时不可避免地会产生振动;随着时间的增加,在阻尼的作用下,轮对的振动幅值在逐渐减小,当到达B点时,轮对基本处于稳态滚动状态;根据Zhao 等人[10]研究的结论,当轮轨垂向力的波动幅值除以轮对的静轴重小于10%时,即可认为车辆达到稳态运动状态,有限元结果即可用于相应的计算分析,从B点到C点,轮轨垂向力基本平稳,其最大波动幅值除以单个车轮的静轴重约为5.5%,且轮轨垂向力在125 kN 附近波动,与轴重相吻合,表明所建模型可以用来进行进一步的分析计算。

表1 有限元模型中所用参数

图3 轮轨垂向力
3 轮轨接触状态
由于不同轨底坡会导致轮轨接触点的位置及接触斑几何形态的改变,这一改变可能导致疲劳裂纹萌生位置及萌生时间的改变,因此,分析不同轨底坡时的轮轨接触状态对预测疲劳裂纹的萌生起着重要的作用。我国的重载铁路中,轨底坡多数设置为1∶40,但是在一些早期的线路中,仍存在轨底坡为1∶20 的情况,因此考虑轨底坡分别为1∶40,1∶30,1∶20和1∶10的情况。
首先,分析轮对相对于轨道发生一定范围横移时的轮轨接触状态。轮背内侧距为1 353 mm,轨距为1 435 mm,以此确定车轮与钢轨的初始接触位置。以轮轨初始接触位置为起点,轮对分别向左右移动,移动的最大距离为12 mm,并用直线将车轮上的点与钢轨上的对应点相连,软件截屏得到整个移动范围内的最短接触长度如图4所示。图中:红线为轮对没有横移时的轮轨接触状态。

图4 不同轨底坡时轮轨接触状态(单位:mm)
从图4可以看出:轨底坡为1∶40 时,轮轨接触位置主要位于钢轨的轨距角处,集中在距轨距边9~22 mm 范围内;轨底坡为1∶30 时,轮轨接触位置主要还是集中在轨距角处,但是在轨顶处也出现了少量的分布,且集中在距轨距边12~27 mm范围内;轨底坡为1∶20 时,轮轨接触位置在轨顶处及轨距角处均有分布,并且主要集中在轨顶的两边,距轨顶2 侧13 mm 范围内;轨底坡为1∶10时,轮轨接触位置在轨顶外侧,距轨距边16~21 mm范围内。可以看出,改变轨底坡将改变轮轨接触位置,而轨底坡为1∶40 时轮轨接触位置主要集中在轨距角处,这一情况也有可能是钢轨斜裂纹的萌生因素,需要做进一步的分析。
通过分析车轮与钢轨在初始接触位置沿着轨道直线运动的情况,得到不同轨底坡时钢轨的压力分布如图5所示,从而得到不同轨底坡时的法向节点力和接触斑形态,如图6所示。图6中:上半部分为接触斑内的法向节点力,映射到下平面中的为接触斑的形态。

图5 不同轨底坡时钢轨压应力分布
从图5和图6可以看出:轨底坡为1∶40 时,轮轨接触斑不在钢轨轨顶处,而是偏向于轨距角处,接触斑呈椭圆形,其长半轴和短半轴的长度分别为9.0 和4.5 mm,最大压应力为1.20 GPa;轨底坡为1∶30 时,接触斑的位置比轨底坡为1∶40时更靠近轨顶,接触斑的面积增大,不再是标准的椭圆形,最大压应力略微降低,为1.16 GPa;轨底坡为1∶20 时,接触斑不再是1 个椭圆形,而变成了1 个带状分布的图形,整个接触斑位于轨顶处,在轨顶2 侧有2 个峰值,最大压应力大幅降低,为0.70 GPa;轨底坡为1∶30时,接触斑从钢轨轨顶内侧转移到钢轨轨顶外侧,最大压应力为1.31 GPa;当轨底坡为1∶20时,车轮和钢轨发生了共形接触,导致接触面积增大,同时压应力大幅降低,这种轨道参数与LM型车轮更为匹配。
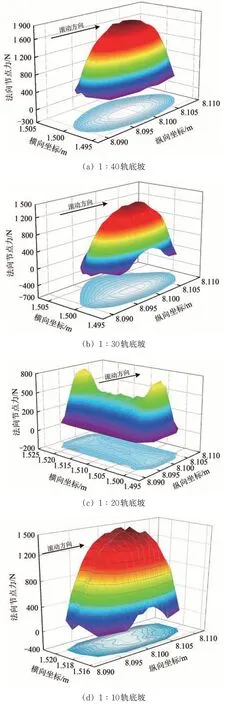
图6 不同轨底坡时法向节点力和接触斑形态
最后,为了验证上述的轮轨接触状态,仿真得出不同轨底坡时车轮与钢轨的接触区域,且由于轮轨接触区内单元的变形为0.05 mm,仅选择车轮与钢轨接触距离小于0.05 mm 的线段,结果如图7所示。从图7可以看出:图(a),图(b)和图(d)中的轮轨接触区域均靠近轨距角处;图(c)中均匀分布在轨顶的2 侧,且接触区域远大于图(a),图(b)和(d),这一结果也与图5中的结果相一致。

图7 不同轨底坡时轮轨接触区域
4 钢轨疲劳裂纹萌生影响因素
为了找到疲劳裂纹萌生平面,将应力应变矩阵进行旋转,旋转矩阵A中θ和ϕ的变化范围均为0°~360°,步长为5°。分析轨底坡为1∶40、摩擦系数为0.5 的情况,提取出计算区域内各单元随时间变化的应力应变数据,代入式(1)中进行计算,求出各单元在不同旋转角度下的疲劳参量如图8所示。
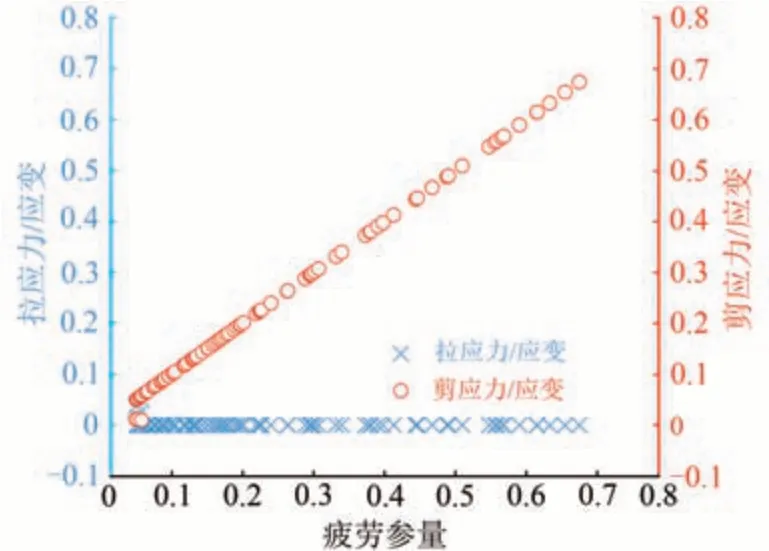
图8 各单元疲劳参量
图8中左侧纵坐标数值为式(1)中的拉应力/拉应变部分;右侧纵坐标数值为式(1)中的剪应力/剪应变部分。从图8可以看出:当疲劳参量FP小于0.1 时,有部分单元是由拉应力及剪应力共同作用;当FP大于0.1 时,单元受力以剪应力为主;图8中,当单元受到压应力的作用时,式(1)中拉应力/拉应变部分的值为0,疲劳参量值由剪应力/剪应变部分决定;当单元受到拉应力的作用时,式(1)中剪应力/剪应变部分近似为0,疲劳参量值由拉应力/拉应变部分决定。在各单元中,疲劳参量的最大值为0.67,拉应力/拉应变为0,因此寿命预测公式选择剪切型裂纹寿命预测模型,即式(7)。
在单元疲劳参量为最大值时,对应的旋转角度为θ=40°,ϕ=10°。将所得角度与在实际线路中观察到的裂纹形态进行对比,结果如图9所示。图中:行车方向水平向右,裂纹面的垂线用虚线表示,与X轴的角度为θ,与Z轴的角度为ϕ。从图9可以看出,计算结果中的角度与实际裂纹的形态较为一致。

图9 裂纹角度
分析得到各单元的疲劳参量如图10所示。图中:红线轮廓为轨头廓形,柱状图的长度为疲劳参量。从图10可以看出:疲劳参量最大值发生于轨顶以下1.96 mm 处,到轨距角的水平距离为21.5 mm,这一结果与现场观测到的斜裂纹基本一致。
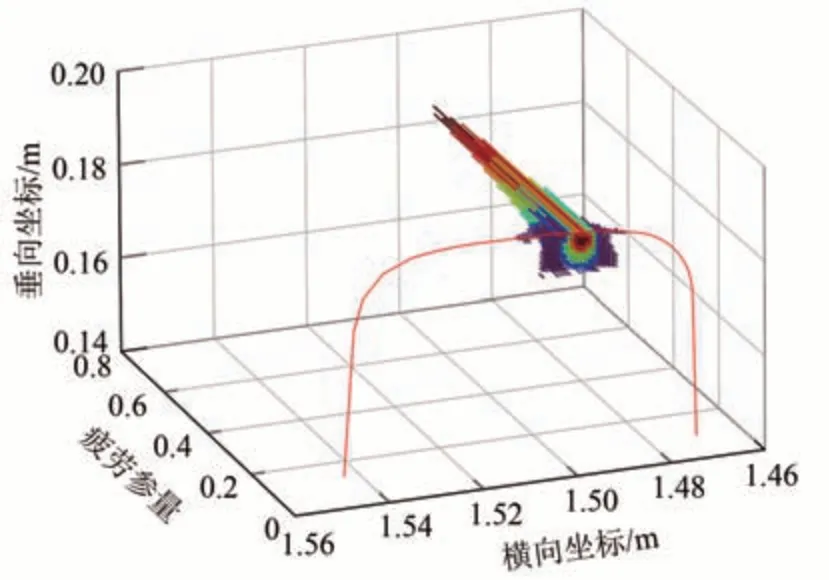
图10 各单元的疲劳参量
对不同轮对横移量时裂纹的萌生进行分析,将轮对向外轨方向进行横移,横移量分别为6 和12 mm,轮对横移后的轮轨接触状态如图11所示。从图11可以看出:当轮对横移量为12 mm 时,接触斑位于轨距角处,接触班呈长条状,最大压力为1.83 GPa;轮对横移量为6 mm 时,接触斑呈近似圆形,最大接触压力为953 MPa。

图11 不同轮对横移量时轮轨接触状态
不同轮对横移量时对应的疲劳参量如图12所示。从图12可以看出:当轮对向外轨侧横移时,疲劳参量在增大,更容易导致裂纹的萌生。

图12 不同横移量的疲劳参量
由于疲劳参量为最大值时,对应单元的拉应力/拉应变部分为零,只存在剪应力/剪应变部分,因此采用剪切型寿命预测公式,即式(7)进行裂纹萌生寿命分析。材料参数参考Jiang[11]所提供的数据,式中的τ′f,γ′f,b和c分别取为1 015,0.509 4,-0.104 8 和-0.550 1。计算得出在这种情况下,钢轨疲劳裂纹萌生时轮对的通过次数Nf为9.19×105次,通过总重为2 298 万t。由于实际轮轨接触位置是在1 个接触区域内随机变化的,而文中所分析的接触区域是相对固定的,因此实际的萌生寿命比文中预测的要长,文中得出的计算结果是偏于安全的。
采用相同的方法,计算出轨底坡为1∶30,1∶20 和1∶10 时钢轨疲劳裂纹的萌生寿命分别为3 934 万t、9.88 亿t 及3 875 万t,如图13所示。从图13可以看出:轨底坡由1∶40 增加到1∶20 时,钢轨疲劳裂纹的萌生寿命增加;轨底坡由1∶20 增加到1∶10 时,萌生寿命降低,而且轨底坡为1∶20 时的萌生寿命最大,说明LM 型车轮在轨底坡为1∶20 时与75 kg·m-1钢轨更为匹配,此时可以大幅提升裂纹的萌生寿命,提高钢轨的使用时间。
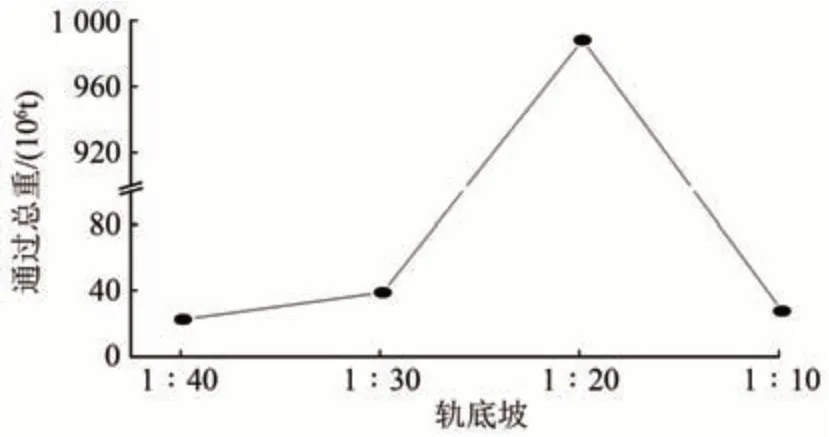
图13 不同轨底坡裂纹萌生寿命
1∶40 轨底坡时不同摩擦系数对钢轨疲劳裂纹萌生寿命的影响结果如图14所示。从图14可以看出:随着摩擦系数的增大,通过总重随之减小,也就是摩擦系数越大越容易导致裂纹提早萌生。

图14 不同摩擦系数对钢轨疲劳裂纹萌生寿命的影响
为了探究这一原因,分析不同摩擦系数下接触斑内节点的最大法向力和最大切向力,结果如图15所示。从图15可以看出:节点最大法向力随摩擦系数的变化不大,节点最大切向力随摩擦系数增大而增大,也就是法向力对裂纹萌生不起主要作用,而切向力越大越容易导致裂纹尽早萌生,切向力是裂纹萌生的主要影响因素。
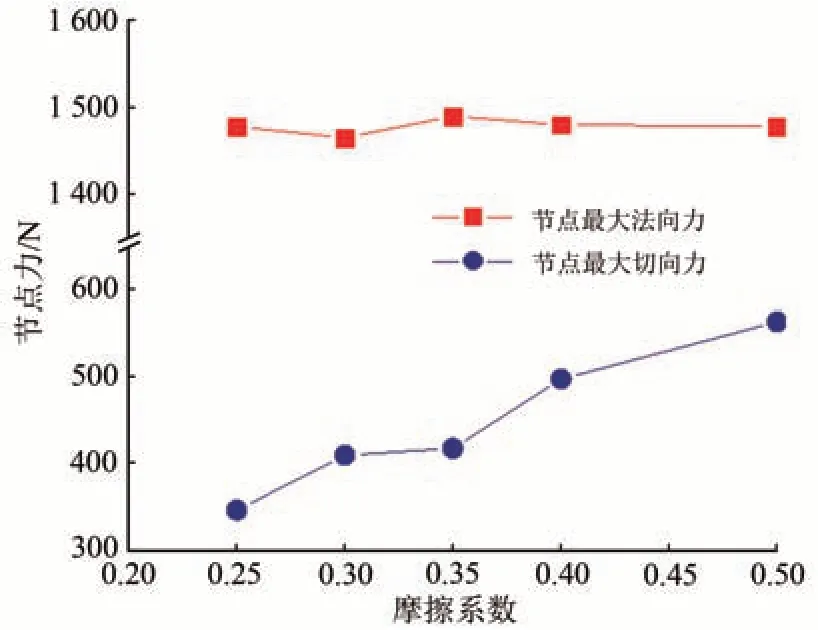
图15 不同摩擦系数时节点最大法向力和最大切向力
5 结 论
(1)轨底坡分别为1∶40,1∶30,1∶20 和1∶10 时,随着轨底坡的增大,接触斑的位置先逐渐向轨顶发展,再向轨顶外侧发展,接触斑的面积先逐渐增大,再降低。车轮踏面为LM 型时,在1∶20轨底坡时与75 kg·m-1钢轨更为匹配。
(2)轨底坡为1∶40 时,疲劳裂纹的萌生位置位于轨顶下方1.96 mm 处,到轨距角的水平距离为21.5 mm,这一结果与现场观测到的斜裂纹基本一致,证明了文中所使用的模型可以有效预测钢轨斜裂纹的萌生。
(3)轨底坡分别为1∶40,1∶30,1∶20 和1∶10 时,随着轨底坡增大,钢轨疲劳裂纹萌生时的通过总重先增大再降低,在轨底坡为1∶20 最大,1∶20的轨底坡可以减缓疲劳裂纹的萌生。
(4)摩擦系数分别为0.25,0.30,0.35,0.40 和0.50 时,随着摩擦系数增大,节点法向力基本不变,节点切向力逐渐增大,疲劳裂纹的萌生寿命逐渐降低,表明摩擦系数越大,切向力越大,疲劳裂纹越容易萌生。
