几类图运算对受控着色数的影响

周洋洋， 许 进

(北京大学 信息科学技术学院， 北京 100871)

若无特殊声明，本文所涉及的图皆指有限、简单和无向图.对于给定图G，分别用V(G)和E(G)表示G的顶点集和边集，G中所含顶点数(|V(G)|)和边数(|E(G)|)分别称为G的阶和规模.对任意v∈V(G)，v的开邻域，记作N(v)，表示G中与顶点v相邻的所有顶点构成的集合，即N(v)={u|uv∈E(G)}.v的闭邻域N[v]=N(v)∪{v}. 顶点v的度数，记作d(v)，是指N(v)中元素的个数.用δ(G)和Δ(G)分别表示G的最小度和最大度，并分别简记为δ和Δ. 设v∈V(G)，S⊆V(G)，如果v与S中的每个顶点都相邻，则称v控制S，也称S被v控制.令S是G的一个顶点子集，如果S中任意两个顶点在G中均不相邻，则称S为G的一个独立集.若V′⊂V，E′⊂E，且E′中每条边的两个端点均在V′中，则称图H=(V′,E′)是图G的一个子图.设H是G的一个子图，如果V(H)=V(G)，则称H是G的生成子图.如果对于子图H中任意两个顶点u和v、u、v在G中相邻当且仅当它们在H中相邻，则称H为G的一个由V′导出的子图，记为G[V′].用Pn=v1v2…vn-1vn表示n个顶点，长度为n-1的路，并用Cn=v1v2…vn-1vnv1表示n个顶点，长度为n的圈，常将长度为n的圈称为n-圈.文中未说明的概念及记号，可参见文献[1].

图G=(V,E)的一个正常k-顶点着色，是指从顶点集V到颜色集{1,2,…,k}的一个映射f，使得G中任意两个相邻的顶点都着不同颜色.事实上，图的k-顶点着色问题等价于将顶点集V(G)划分为k个独立集{V1,V2,…,Vk}，其中Vi={x∈V|f(x)=i}，i=1,2,…,k. 笔者将着相同颜色的顶点的集合称为一个色组.图G的色数，记作(G)，是G的一个正常着色所需颜色数的最小值.一个(G)-着色是G的具有最小基数的顶点着色.

图G的一个控制集是指一个顶点子集S，使得G中每个顶点要么在S中，要么与S中的顶点相邻.图G的控制数，记作γ(G)，是指G的一个控制集的最小基数.

图的着色理论和控制理论是图论中两个非常活跃的重要领域，都有着广泛丰富的研究成果，分别详见文献[2-9].此外，许多学者从多个方面讨论了这两个领域之间的联系，并提出了一些新的概念.

2004年，Chellali等[10]展示了图的色数与一些控制参数之间的关系.Cockayne等（1）Cockayne E,Hedetniemi S,Hedetniemi S M, et al. Dominator partitions of graphs, Unpublished manuscript, 1979.在1979年引入并介绍了图的控制划分的概念，在此推动下，2006年，Gera等[11]提出了控制着色的概念.

图的控制着色是一个正常顶点着色，使得每个顶点都控制至少一个色组(可能是顶点自身所构成的色组).图的控制着色数，记作d(G)，是指图G的一个控制着色中色组的最小值.

在控制着色的基础上，Kazemi[12]在2015年提出了全控制着色的概念，全控制着色是指一个正常顶点着色，使得每个顶点都与某个色组中的所有顶点相邻.关于控制着色和全控制着色的更多结论，参见文献[13-21].

2015年，Merouane等[22]提出了受控着色的概念.图的受控着色是一个正常顶点着色，使得每个色组都被至少一个顶点控制.图的受控着色数，记作dom(G)，是指图G的一个受控着色所需颜色数的最小值.

基于控制着色和受控着色的研究，笔者在文献[23]中提出了统治着色的概念，并研究得到了一些基本性质和结论.

图的统治着色，是指一个正常顶点着色，使得每个顶点都控制至少一个色组(可能是顶点自身所构成的色组)，且每个色组都被至少一个顶点控制.图的统治着色数，记作dd(G)，是指图G的一个统治着色所需颜色数的最小值.

基于上述概念，学者们自然地关注了另一个有趣的问题：当对图G实施某些运算时，这些参数会发生什么变化？针对这个问题，Ghanbari等[24]在2016年研究了某些运算对全控制着色数的影响.2018年，Alikhani等[25]讨论了一个图的k-细分图的全控制着色数.2019年，Alikhani等[26]在研究几类特殊图的受控着色数的同时，还讨论了它们的受控稳定临界数，即使得受控着色数dom(G)改变所需删除的顶点(边)数的最小值.同年，笔者在文献[27]中研究了一些图运算对统治着色数的影响.

1 删除顶点和边

顶点和边的移除是图运算中最基本的运算，本节讨论删除顶点和删除边运算对图的受控着色数dom(G)的影响.

设v是G中任意顶点，e是G中任意一条边.G-v是通过在图G中删除顶点v以及所有与v相关联的边所得到的图.G-e是通过在G中删除边e所得到的图.

定理1 设G是一个连通图，v∈V(G)且v不是割点，则

dom(G)-1≤dom(G-v)≤dom(G)+d(v)-1.

证明先证明左边不等式.给定G-v的任意受控着色，考虑G的受控着色如下：在G-v中添加顶点v和所有相应的边，给顶点v着一种新的颜色i，其他顶点着色不变.顶点v所在的色组可被v的任意一个邻点控制，而其他色组仍由原来的顶点控制，这样得到了图G的一个受控着色.于是，dom(G)≤dom(G-v)+1.

下面证明右边部分.对于图G的任一受控着色，假设顶点v着颜色i，则有下面两种情况：

情况(1):存在其他顶点着颜色i. 如果存在色组仅被顶点v控制，那么给此色组中的每个顶点一种新的颜色.显然，至多有d(v)个这样的顶点.因为v不是割点，每一个新着色的顶点作为一个色组必然被其他邻点(除v外)控制，而其他色组仍由原来的顶点控制.于是得到了G-v的一个受控着色，且dom(G-v)≤dom(G)+d(v)-1. 如果不存在上述性质的色组，则由图G原来的着色即可得到G-v的一个受控着色，且dom(G-v)≤dom(G).

情况(2):不存在其他顶点着颜色i. 按照情况(1)的分析，如果存在色组仅被顶点v控制，则dom(G-v)≤dom(G)+d(v)-2. 否则，dom(G-v)≤dom(G)-1.

定理得证.

定理2 设G是一个连通图，e∈E(G)且e不是割边，则

证明设e=uv∈E(G). 首先，证明左边不等式.考虑G-e的一个受控着色，若在G-e中添加边e，则存在两种情况：

情况(1):顶点u和v在G-e的受控着色中着相同颜色.对u和v中之一着新的颜色i，其他顶点着色保持不变，这样就得到了G的一个受控着色，且满足dom(G)≤dom(G-e)+1.

情况(2):顶点u和v在G-e的受控着色中着不同颜色.那么，G-e的受控着色也是G的受控着色，于是dom(G)≤dom(G-e).

下面证明右边不等式.考虑G的一个受控着色，假设u∈Vi，v∈Vj，即顶点u着颜色i，顶点v着颜色j. 于是，存在下面三种情况：

情况(1):顶点u不控制色组Vj，且顶点v不控制色组Vi. 在这种情况下，G的受控着色也是G-e的一个受控着色.从而，dom(G-e)≤dom(G).

情况(2):顶点u控制色组Vj，而顶点v不控制色组Vi. 根据定义，u与Vj中每个顶点都相邻，而Vi必由其他顶点控制.在图G-e中，给顶点v一种新的颜色k. 由于e不是割边，G-e是连通图且顶点v有其他邻点.那么，v自身构成的色组必被其他邻点控制，色组Vj{v}被顶点u控制，其他保持不变，这样得到了G-e的一个受控着色，且dom(G-e)≤dom(G)+1.

情况(3):顶点u控制色组Vj，且顶点v控制色组Vi. 在这种情况下，给顶点u和v分别着新的颜色k和l. 由于e不是割边，则G-e是连通图.在新得到的着色中，顶点u和v各自所在的色组都会由它们其他的邻点所控制.又因其他顶点着色不变，这个新得到的着色即是G-e的一个受控着色，且dom(G-e)≤dom(G)+2.

定理得证.

2 收缩顶点和边

设图G=(V,E)，S⊆V是一个顶点子集，在G中收缩S，记作G∘S，是通过将S中的所有顶点替换为一个新的顶点，并将原来与S中顶点相关联的边均与这个新的顶点关联所得到的图.特别地，当S={u,v}时，有下面两种情况：

(1) 顶点u和v相邻，即e=uv∈E(G). 在图G中收缩边e=uv，记作G∘e，是通过删除边e，并将顶点u和v替换为一个新的顶点，使得原来与u或v相邻的顶点均与这个新的顶点相邻而得到的图.收缩边运算，简称为缩边运算，如图1所示，其中顶点周围的黑色省略号标记表示可能存在边与该顶点关联.

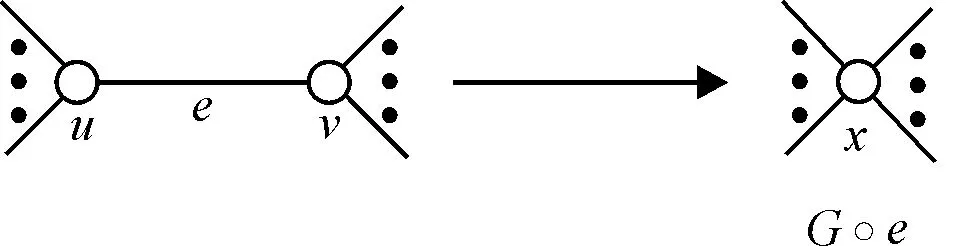
图1 缩边运算Fig.1 The edge contraction operation

(2)顶点u和v不相邻.将此时的收缩运算记作G∘ {u,v}，简称为缩点运算，如图2所示.

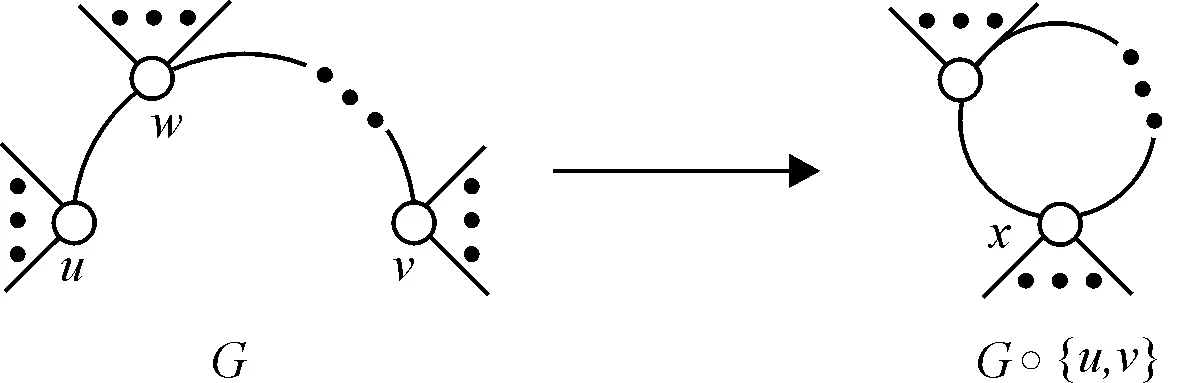
图2 缩点运算Fig.2 The vertex contraction operation

定理3 设G是一个连通图，e∈E(G)，则

证明设e=uv∈E(G). 首先，证明左边不等式.考虑G∘e的一个dom(G∘e)-受控着色.通过在G∘e中添加删除的顶点以及所有相应的边，得到图G. 将e的端点的原来的着色删除，并对顶点u和v分别着新的颜色k和l，其他顶点着色不变.易验证，这样得到的是G的一个受控着色，且dom(G)≤dom(G∘e)+2.

再证明右边不等式.考虑G的一个dom(G)-受控着色f，其中f(u)=i，f(v)=j. 令x是替换u和v的新顶点.下面构造G∘e的受控着色.给顶点x着新的颜色k，其他顶点着色不变.顶点x自身构成的色组可由其任意邻点控制，于是得到了G∘e的一个受控着色，且dom(G∘e)≤dom(G)+1.

定理得证.

定理4 设G是一个连通图，u和v为G中任意两个不相邻的顶点，则

证明设u，v为G中任意两个不相邻的顶点.首先,证明左边不等式.考虑G∘ {u,v}的一个dom(G∘ {u,v})-受控着色.在G∘ {u,v}中添加删除的顶点以及相应的边，得到图G. 将u和v原来的颜色删除，并分别给它们着新的颜色k和l，其他顶点着色不变.易验证，这是G的一个受控着色，且dom(G)≤dom(G∘ {u,v})+2.

接着，证明右边不等式.考虑G的一个dom(G)-受控着色f，基于f来构造G∘ {u,v}的受控着色.令x是替换u和v的新顶点.给x着新的颜色k，其他顶点颜色保持不变.易验证，这样得到的是图G∘ {u,v}的一个受控着色，且dom(G∘ {u,v})≤dom(G)+1.

定理得证.

3 边细分

设G是一个连通图，k是一个正整数.G的k-细分图，记作Sk(G)，是通过将G中的每条边替换成长度为k的路而得到的图.对于每条边e=vivj∈E(G)，用Pvivj表示替换vivj的k-路，并称Pvivj为超边，Pvivj的任意新顶点都是内部顶点.注意到，如果k=1，则S1(G)=G.

边的细分是一种典型的图运算.本节研究一个图G的k-细分图的受控着色数，以及dom(G)和dom(Sk(G))之间的关系.

定理5 设G是一个含m条边的连通图，k≥2是正整数，则

(m-1)dom(Pk)+dom(Pk+1).

证明首先,证明左边不等式.设e=uv为G中任意一条边，Puv=ux1x2…xk-1v是Sk(G)中替换uv的路，如图3所示.令f是Sk(G)的一个dom(Sk(G))-受控着色，考虑f在导出子图Puv上的限制，记为f′. 由于f是受控着色，端点u(v)要么自身构成色组，要么和其他顶点同在一个色组，都存在邻点控制其所在色组，又因Puv内部顶点的着色不变，那么f′的每个色组也必有顶点控制.因此，f′是Puv的一个受控着色，且dom(Pk+1)≤|f′|≤|f|=dom(Sk(G)).

图3 边细分运算Fig.3 The edge subdivision operation

下面证明右边不等式.设G是一个含m条边的连通图.对任意u∈V(G)，令N(u)={v1,v2,…,vp}，边uvi分别由超边Puvi替换，i=1,2,…,p.类似一般Pk+1的受控着色，可用dom(Pk+1)种颜色给超边Puv1的顶点着色.对Puvi(i=1,2,…,p)的顶点着色，使得顶点u的着色唯一(即u在Puvi(i=2,…,p)中的着色均与Puv1中一致)，并且满足

f(Puvi)∩f(Puvj){f(u)}=∅，

其中,i,j=1,2,…,p，i≠j，f(Puvi)表示Puvi中顶点的颜色的集合.这样，用至多(p-1)dom(Pk)+dom(Pk+1)种颜色得到了Puvi(i=1,2,…,p)的一个受控着色.接着，考虑与vi(i=1,2,…,p)相关联的边所对应的未着色的超边.继续重复上述过程，直到Sk(G)的所有顶点均被着色.注意到，某些位于圈上的顶点会被重复着色，但这不会影响最后结果.容易验证，最后得到的着色是Sk(G)的一个受控着色，且使用了至多(m-1)dom(Pk)+dom(Pk+1)种颜色.因此，右边不等式成立.

定理得证.

4 扩圈运算

本节讨论扩圈运算，以及受控着色数在扩圈运算下的变化.

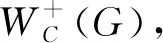
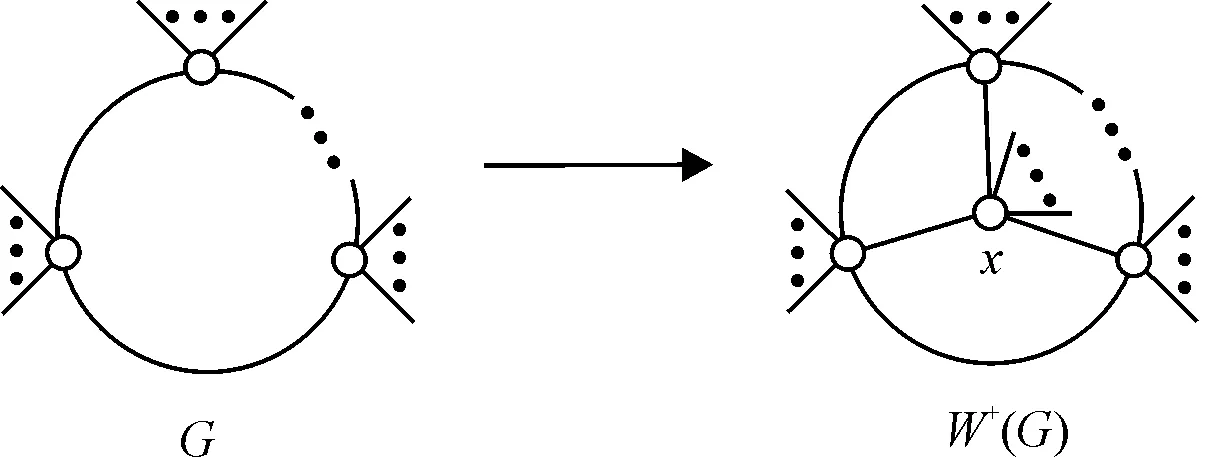
图4 扩圈运算Fig.4 The cycle extending operation

定理6 设G是一个连通图，C是G中任意长度为l(≥3)的圈，则

证明首先,证明右边不等式.对于G的任意一个dom(G)-受控着色，给中心顶点x着一种新的颜色，而其他顶点颜色不变，这样就得到了W+(G)的一个受控着色.因此，dom(W+(G))≤dom(G)+1.

接着，证明左边不等式.设f是W+(G)的一个dom(W+(G))-受控着色，下面基于f构造G的一个受控着色，在W+(G)中删除顶点x及与它相关联的边，得到图G. 需要考虑那些仅被顶点x控制的色组，显然，这些色组中的元素只可能是圈C上的顶点，因此，只需添加至多l种新的颜色给这些顶点重新着色，就可得到G的一个受控着色.于是，dom(G)≤dom(W+(G))+l.

定理得证.

5 结论与展望