对称逆半群的奇异部分的自同态
2012-12-22黄丽丽杨秀良
黄丽丽,杨秀良
(杭州师范大学理学院,浙江杭州 310036)
对称逆半群的奇异部分的自同态
黄丽丽,杨秀良
(杭州师范大学理学院,浙江杭州 310036)
通过对同态核的讨论和研究,刻画了有限对称逆半群的奇异部分的所有自同态,从而对有限对称逆半群的理论进行有效补充.
对称;奇异;半群;自同态;同余
0 引 言
集合X上的所有部分单变换构成的集合称作X的对称逆半群,记作.集合X上的所有置换构成的集合称作X的置换群,记作.若g,t均为变换,则定义变换got如下:对任意的x∈X,都有got(x)=g(t(x)).易见,当且仅当g(t(x))有意义时,got(x)有意义.为简化记法,可将got记作gt.对称逆半群是半群理论中很重要的一部分,它的许多性质已经被前人所研究.特别的,Schreier[1]证得的所有自同构均为内自同构(即对的任意一个自同构α,存在唯一确定的g∈,使得对任意的t∈,都有α(t)=gtg-1).在此基础上,Schein等[2]讨论了的所有自同态.
以下介绍一些符号和名词.将t∈\Sn的定义域记作dom(t),值域记作im(t).特别的,im(st)⊆im(s).称im(t)的基数为t的秩,即rank(t)=|im(t)|.对任意的x∈X,ax={(x,x)}.即ax∈X×X,且只含有一对有序数对(x,x).对任意的Y⊂X,记ΔY={(x,x):x∈Y}.定义0∈\如下:

即dom(0)=φ.称0为\的空变换.

1 主要结果

2 定理证明

y∈X.则αδ(x)=α(y)=z≠y=δ(x).故αδ≠δ.
综上所述,引理得证.
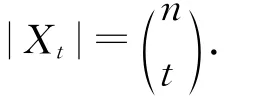


综上所述,定理得证.
[1]Schreier J.Über abbildungen einer abstrakten menge aufihre teilmengen[J].Fund Math,1936,28:261-264.
[2]Schein B M,Teclezghi B.Endomorphisms of finite symmetric inverse semigroups[J].Journal of Algebra,1997,198(1):300-310.
[3]Ganyushkin O,Mazorchuk V.Classical finite transformation semigroups:an introduction[M].London:Springer &Verlag,2009.
The Endomorphisms of the Singular Parts in Symmetric Inverse Semigroup
HUANG Li-li,YANG Xiu-liang
(College of Science,Hangzhou Normal University,Hangzhou 310036,China)
This paper discussed and studied the homomorphic kernel,described all the endomorphisms of the singular parts in finite symmetric inverse semigroup,and supplemented the theory of finite symmetric inverse semigroup.
symmetric;singular;semigroup;endomorphism;congruence
O152.7 MSC2010:43A22
A
1674-232X(2012)06-0524-04
10.3969/j.issn.1674-232X.2012.06.010
2011-12-01
杨秀良(1963—),男,教授,主要从事半群代数研究.E-mail:yxl@hznu.edu.cn
