几类确定型网络模型的最多叶子生成树数目和最大独立集
2020-08-04马飞,姚兵
马 飞, 姚 兵
(1.北京大学 信息科学技术学院, 北京 100871; 2.西北师范大学 数学与统计学院, 甘肃 兰州 730070)
1 引言及定义
众所周知,复杂系统在人们生活的世界中无处不在,如科学家合作网络、细胞中新陈代谢网络、机体中蛋白质交互网络、生物链中捕食-被捕食网络和万维网等[1-3]. 为了揭示这些复杂系统背后的演化机理,以及刻画这些系统上发生的动力学行为,过去的几十年,研究者们已经提出了很多数学模型并发展了许多研究技术,其中最为知名的是Erdös等[4]和Newman等[5]在20世纪五六十年代提出的ER-模型. 特别地,随着近二十年复杂系统研究的发展,一个崭新的交叉学科——复杂网络已经掀起了网络研究热潮.作为一个新兴的、强有力的研究工具,复杂网络可以很方便地描述现实世界中的众多复杂系统,以此为载体帮助人们揭示了复杂系统中很多普适的规律[6].
尽管ER-模型能够刻画复杂网络中存在的随机性,但是却在某些方面展现出一些与真实网络相异的结构特点.研究表明,ER-模型中节点的度分布服从 Poisson分布,即大量节点的度值集中在度平均值附近.另外,大量的网络实例却展示网络中节点的度分布近似地服从重尾分布,包括幂律分布、指数分布等[7-8].所以,发展新的理论模型以适应真实网络研究已经势在必行.1999年,Barabási等[9]提出服从幂律分布的BA-模型,并提供了两条现实网络演化的简单规则:择优连接和增长.自此以后,为了模拟网络中的幂律分布特征,建立了大量的数学模型,其中一部分是随机模型[10-12],另一部分是确定模型[13].
一般地,复杂网络模型可以用数学语言描述成图论中的图G(V,E)[14].其中,V表示网络中的节点集合,E代表了网络中的边集合,相应地,符号|V|和|E|分别被定义成网络的节点数和边数.正因如此,复杂网络的研究刺激了传统图论的研究,为图论的发展注入了新的活力.同时,图论中一些经典的研究问题为开展复杂网络的深入研究提供了理论支撑和科学依据.例如,生成树是图论中研究图拓扑性质的一个重要参数,可以作为一个结构参数来刻画网络在受到攻击时自身所表现出来的结构稳定性.尽管任意一个图的生成树数目可以通过Matrix-Tree定理得到[14],但是为一些特殊图类建立便捷的生成树计数技术也是一个有趣且富有挑战的研究课题.另一个图论中的经典问题就是寻找任意指定图的最大独立集,如此一个指标可以帮助研究者优化网络自身的拓扑结构.实际上,这是一个NP问题.但在部分图类的研究中,最大独立集问题却是P问题.
为了进一步体现复杂网络和图论之间强大的关联性和互补性,一些为模拟部分复杂网络所建立的理论模型将被介绍,尽管这些模型中的一些结构参数已经在其他的文献中被详细讨论过,但这里主要研究这些模型的最多叶子生成树以及最大独立集,采用这些拓扑参数去更好地体现模型之间的结构差异性,为构建更合理的模型提供理论依据.
本文在此规定: 所有讨论的模型都是简单连通图,图和网络会被不加区分地交替使用.
定义1给定一个图G(V,E), 一个包含G的所有节点的连通子图T是一棵生成树,当且仅当T所包含的边数恰等于节点数减一.为了方便起见,让所有的生成树构成树集合T.对于一棵生成树T∈T而言,若用记号LT表示其叶子节点数的数目,那么,图G的最多叶子生成树T便有如下性质:
∀T∈T,LT≤LT.
同理,所有最多叶子生成树构成的集合记作Λ, 其基数就是|Λ|.
定义2给定一个图G(V,E)和一条边uv∈E, 删除任意一条边后节点u和v分属两个子树的所有生成树构成集合Ωuv,相应地,其基数被定义为|Ωuv|.
定义3 给定一个图G(V,E), 一个节点子集A⊆V被称为独立集,当且仅当不存在一条边e∈E连接了集合A中的任意一对节点.所有独立集构成一个集合A.特别地,若元素A∈A满足如下性质:
∀A∈A, |A|≤|A|,
则称其为图G(V,E)的最大独立集,|A|称为图G(V,E)的独立数,简记作Φ.所有最大独立集构成的集合记作Ψ, 相应地,其基数定义为|Ψ|.
2 网络的构造
2.1 模型 N1(t)
初始,一条边被选择作为模型N1(0).在t=1时刻,模型N1(1)可以通过连接一个外部节点到模型N1(0)的两个节点得到.接下来,当t≥2时,模型N1(t)就可以通过采取和上述一样的构造方法获得,具体地说,对模型N1(t-1)的每一条边都添加一个新的外部节点,然后用两条边把这个新节点连接到那条边的两个节点上.为了使这里的构造方法更容易理解,图1展示了构造模型N1(t)的前四个阶段.
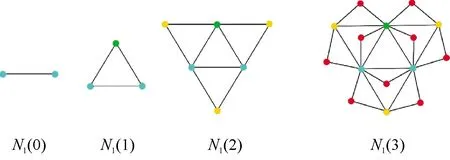
图1 网络模型N1(t)生成过程的前四个阶段Fig.1 The first four generations of model N1(t)
鉴于上述的构造方法,模型N1(t)的节点数|V1(t)|和边数|E1(t)|满足如下的递推方程:
|V1(t)|=|V1(t-1)|+|E1(t-1)|,
|E1(t)|=3|E1(t-1)|
(1)
将初始值|V1(0)|=2和|E1(0)|=1代入方程(1)便可以计算得到
(2)
显然,模型N1(t)是稀疏,因为它的平均度的极限是一个常数,如下:
(3)
实际上,模型N1(t)已经被其他的研究者进行了广泛的研究.例如,在文献[15]中,作者已经分析了模型N1(t)的其他一些包括度分布在内的结构参数.研究表明,模型N1(t)的度分布服从幂律分布
P1(k)~k-γ1,γ1=1+ln3/ln2.
因此,和大多数真实的网络一样,其展现出了无标度特征.
2.2 模型N2(t)
类似于模型N1(t)的构造,这里将介绍模型N2(t)的具体构造过程.实际上,模型N2(t)也是通过循环迭代的方式产生的,具体细节如下:
在t=0时,模型N2(0)仍是一条连接了两个节点的边.在t=1时,模型N2(1)和模型N1(1)是一样的,都是将一个外部节点连接到一条初始边的两个节点.类似地,在t=2时,模型N2(1)可以采用构造模型N1(1)方式得到.然而,在t>2时,模型N2(t)是通过仅仅给上一个时刻新出现的每一条边引入一个外部节点,并用两条边连接到该条边的两个节点生成的.最终,如此一个细微改变的构造方式将产生一个与模型N1(t)截然不同的模型.为了便于理解,构造模型N2(t)的前四个阶段如图2所示.
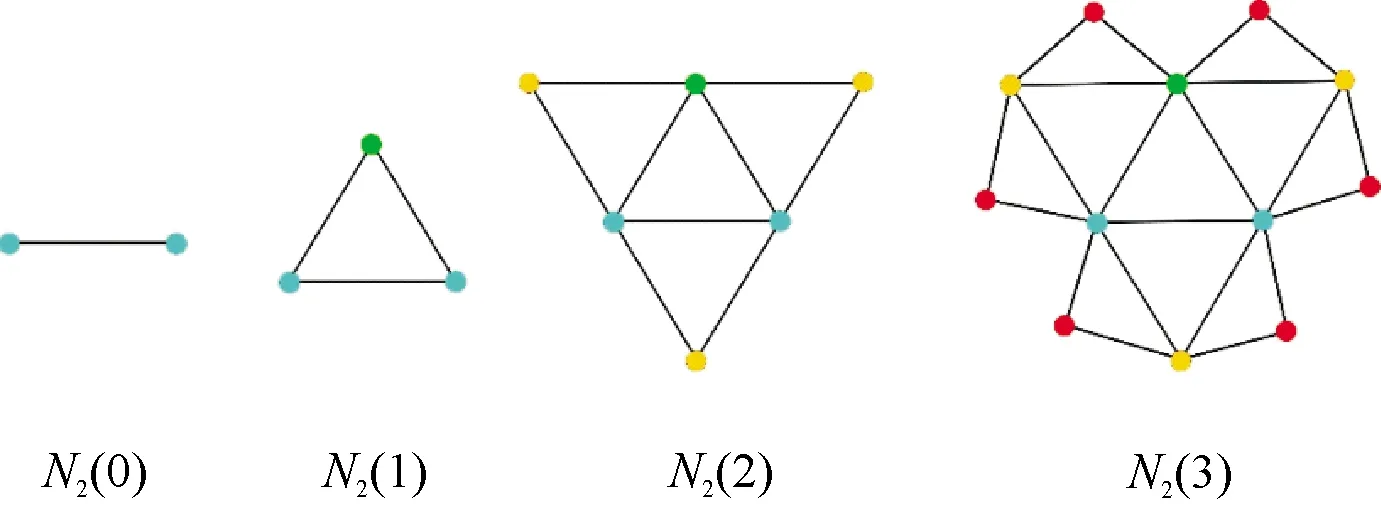
图2 网络模型N2(t)生成过程的前四个阶段
循环迭代生成模型N2(t)的构造方式有助于建立一组被其节点数|V2(t)|和边数|E2(t)|满足的方程组,如下:
|V2(t)|=|V2(t-1)|+|ΔV2(t)|,
|E2(t)|=|E2(t-1)|+|ΔE2(t)|
(4)
这里,符号ΔV2(t)和ΔE2(t)分别表示了t时刻产生的点集合和边集合,相应地,|ΔV2(t)|和|ΔE2(t)|表示对应的点数和边数.基于模型N2(t)的构造方式,可以发现它们满足如下的递推关系:
|ΔV2(t)|=|ΔE2(t-1)|,
|ΔE2(t)|=2|ΔE2(t-1)|
(5)
将初始值|ΔE2(2)|=6代入方程(5)的第二个式子中便可以计算得到:|ΔE2(t)|=3×2t-1.进而,可以准确计算节点数|V2(t)|和边数|E2(t)|(t≥1)如下:
|V2(t)|=3×2t-1, |E2(t)|=3×2t-3
(6)
基于上述的计算结果,模型N2(t)很容易被证明具有稀疏性,这是因为它的平均度k2满足以下方程:
(7)
至此,可以发现模型N2(t)和模型N1(t)具有相同的平均度.另一方面,正如文献[16-17]所指,模型N2(t)是一个度分布服从指数分布的网络模型,其具体形式如下:
基于上述两个模型,便证实了一个显然的事实,平均度是一个很平凡的研究网络的度量指标.度分布便可以作为一个进一步细化的研究指标,帮助人们更好地区分不同的网络模型.尽管,幂律度分布已被证实广泛存在于许多复杂网络中,但是,生活中也不乏满足指数度分布的网络模型,如经典的WS-小世界网络模型[18].
2.3 模型N3(t)
现将主要致力于模型N3(t)的具体构造.实际上,这个模型在二十年前已经被Ravasz等[19]提出来了,他们的目的是为了阐释网络中出现的等级结构,具体的构造细节可参见文献.这里,为了体现文章的可读性和完整性,介绍模型N3(t)的一个简单构造过程如下:
在t=0时,模型N3(0)是一个孤立的节点,为了便于后面叙述,这个节点可以被标记成h0;t=1时,将模型N3(0)复制两份,即添加两个新节点,然后用边将这两个节点连接到节点h0上,而后,便得到了模型N3(1),此时,节点h0将被重新标记作h1;以此类推,在t≥2时,首先将模型N3(t-1)复制两份,然后用边将这两个模型最底层的节点都连接到模型N3(t-1)的节点ht-1上,进一步,更新节点ht-1的标号为ht,至此,可以得到模型N3(t).为了便于理解,用图3具体展示构造模型N3(t)的前四个阶段.

图3 网络模型N3(t)生成过程的前四个阶段
基于如此一个构造方式,模型N3(t)的节点数|V3(t)|和边数|E3(t)|便可以满足如下一组方程:
|V3(t)|=3|V3(t-1)|,
|E3(t)|=3|E3(t-1)|+2t
(8)
进一步,将初始值|V3(0)|=1和|E3(0)|=0代入上述方程便可得到如下等式:
|V3(t)|=3t, |E3(t)|=2×3t-2t+1
(9)
同理,可计算模型N3(t)的平均度如下:
(10)
这就表明,模型N3(t)也是稀疏的.
正如文献[19]已经证实的,模型N3(t)也是一个服从幂律度分布的网络模型,具体如下:
P3(k)~k-γ3,γ3=1+ln3/ln2.
至此,文中要讨论的三个确定型网络模型已经都建立了,一些基本的结构参数也解析得到了.基于它们各自具体的构造过程,这里需要注意以下几点:①三个模型都是稀疏的,并且它们的平均度在极限下都是同一个不变的常数4;②三个模型都是平面图;③三个模型都具有自相似性;④度分布一样的模型可以有不同的拓扑结构.
3 主要结果
这一节主要讨论上述三个模型的一些结构参数.第一部分关注模型的最多叶子生成树,第二部分讨论模型的最大独立集.
3.1 最多叶子生成树的数目
命题1模型N1(t)的最多叶子生成树S1(t)具有的叶子数L1(t)为
(11)
证明当t=0,1时,方程(11)很容易被证实,因此这里略去具体的细节.接下来,当t≥2时,欲证明方程(11)成立,则需建立如下的等式
L1(t)=|V1(t)|-|V1(t-2)|
(12)
为证明上式成立,依据节点进入网络的时间,下面将考虑三类情况.
情形1t时刻进入模型N1(t)的节点一定是最多叶子生成树S1(t)的叶子.
假设t时刻进入模型N1(t)的节点v不是最多叶子生成树S1(t)的叶子,那么它必然连接了两个更早时刻进入模型的节点u和w. 显然,这两个节点u和w中至多只能有一个节点成为树S1(t)的叶子.
情形1.1 当节点u和w都不是叶子节点时,根据模型N1(t)的构造方式,在删除边uv后, 添加一条新边uw便可以得到一个新的树S1(t)′.如此一来,树S1(t)′的叶子数比树S1(t)的叶子数多1.假设不成立,原命题为真.
情形1.2 不失一般性,假设节点u是叶子节点,依据模型N1(t)的构造方式,同上述情况一样,在删除边uv后, 添加一条新边uw便可以得到一个新的树S1(t)″.显然,树S1(t)″的叶子数比树S1(t)的叶子数多1. 这与S1(t)是最多叶子生成树矛盾,原命题为真.
至此,情形1是真的.
情形2t-1时刻进入模型N1(t)的节点一定是最多叶子生成树S1(t)的叶子.
类似地,假设情形2为假,即:t-1时刻进入模型N1(t)的节点u不是最多叶子生成树S1(t)的叶子,那么,根据模型N1(t)的构造方式,在t时刻不妨设连接节点u的四条边依次为:uw1、uw2、uv1和uv2.不失一般性,假设节点v1和v2是t时刻进入模型N1(t),那么,根据情形1可知,它们必为树S1(t)的叶子节点,因此,树S1(t)中必包含路w1uw2.此时,可以删除边uw1或者边uw2, 然后再添加边w1w2, 这样就可以构造出一个新树S1(t)′. 显然,树S1(t)′的叶子数比树S1(t)的叶子数多1. 故而,假设不成立,情形2为真.
通过情形1和情形2,如下讨论第三类情形.
情形3t-1时刻以前进入模型N1(t)的节点一定不是最多叶子生成树S1(t)的叶子.
不失一般性,这里只证明t-2时刻进入模型N1(t)的节点u一定不是最多叶子生成树S1(t)的叶子, 更早时刻节点的情形可以通过类似的证明得到.根据模型N1(t)的构造方式,一定存在一个长度为3的圈C1(t):uvwu, 其中节点v在t-1时刻进入模型N1(t),节点w在t时刻进入模型N1(t).如果节点u是一个叶子节点,那么这三个节点便都是最多叶子生成树S1(t)的叶子,这是不可能的,因为节点w的度等于2.
综上知,方程 (12) 是成立的.进一步,命题1为真.
命题2模型N1(t)的最多叶子生成树S1(t)的数目|Λ1(t)|为
(13)
这里,符号Γ1(t-2)表示模型N1(t-2)的生成树数目.
证明命题2可以通过命题1得到.
显而易见,为获得t≥3时刻|Λ1(t)|的显示表达式,必须计算出Γ1(t-2).以下采用文献[20]的技术来获取Γ1(t)的具体表达式.
考虑到模型N1(t)的自相似性和定义2,对于连接两个最大度节点的任意一条边可设参数|Ω1(t)|, 进一步可以得参数所满足的递推公式:
Γ1(t)=3Γ1(t-1)2|Ω1(t-1)|,
|Ω1(t)|=2|Ω1(t-1)|2Γ1(t-1)
(14)
经过简单的运算后,Γ1(t)的具体数值解如下:
(15)
鉴于类似的构造方式,可以直接得到如下的两个命题.
命题3模型N2(t)的最多叶子生成树S2(t)具有的叶子数L2(t)为
(16)
命题4模型N2(t)的最多叶子生成树S2(t)的数目|Λ2(t)|为
(17)
这里,符号Γ2(t-2)表示模型N2(t-2)的生成树数目.
采用同样的计算方法[20],Γ2(t)的解析值可被计算得
(18)
命题5模型N3(t)的最多叶子生成树S3(t)具有的叶子数L3(t)为
(19)
证明由于模型N3(t)具有等级结构,因此,连接两个叶子节点的节点一定不是最多叶子生成树S3(t)中的叶子节点.其次,不失一般性,模型N3(t)最底层中与一个度为2的节点w相关联的任意一对节点u和v可能同时为最多叶子生成树S3(t)的叶子节点,亦不可能同时为最多叶子生成树S3(t)的非叶子节点.假设节点u和v同时为叶子节点,那么与它们相关联节点w将是一个孤立节点,这恰恰与生成树的概念矛盾.另一方面,假设节点u和v同时为最多叶子生成树S3(t)的非叶子节点,根据树的定义,不妨设节点w与节点u相接,与度为kv的节点v相接的节点依次被记作y1,y2,…ykv.在删除边vy1,vy2,…,vykv-1后,添加边uy1,uy2,…,uykv-1便可获得一个生成树S′3(t),显然树S′3(t)的叶子数比树S3(t)的叶子数多1,这与树S3(t)是最多叶子生成树矛盾.
为此,模型N3(t)的最多叶子生成树S3(t)中的叶子数L3(t)满足如下递推关系式:
(20)
在初始条件L3(1)=2下,通过简单的计算便可以得到
L3(t)=2×3t-1.
命题6模型N3(t)的最多叶子生成树S3(t)的数目|Λ3(t)|为
(21)
这里,当t>2时,|Λ3(t)|的显示表达式仍未获得.因此,其可作为未来研究中的一个待探讨问题.
3.2 最大独立集及独立数
命题7模型N1(t)的独立数Φ1(t)为
(22)
当t=0,1,2时,方程(22)能够通过枚举法被证明.下面给出t≥ 2时的一个简单证明.
证明预证明方程(22)在t≥ 2时成立,只需证明模型N1(t)的最大独立集中不包含t时刻之前进入的所有节点.不失一般性,假设模型N1(t)的一个最大独立集 A1(t)包含了一个i(0≤i
基于此,最大独立集中元素的个数便满足:
Φ1(t)=|V1(t)|-|V1(t-1)|=3t-1.
上述证明陈述了一个显然的命题如下:
命题8模型N1(t)的最大独立集的数目|Ψ1(t)|为
(23)
采用类似的证明技术,可以直接得到两个关于模型N2(t)的最大独立集的命题.
命题9模型N2(t)的独立数Φ2(t)为
(24)
命题10模型N2(t)的最大独立集的数目|Ψ2(t)|为
(25)
命题11模型N3(t)的独立数Φ3(t)为
(26)
证明当t=0时,模型N3(0)就是一个独立节点,因而是一个独立集,独立数就是1.当t≥1时,显然,模型N3(t)中与一对叶子节点连接的节点一定不属于最大独立集,否则,删除该节点,然后添加与它相连接的那对叶子节点将会构造出一个比前面所述的最大独立集恰好多一个节点的独立集,这便与最大独立集的概念相矛盾.这样一来,与该节点相连接的所有节点便属于最大独立集A3(t).根据模型N3(t)的等级属性,节点集合A3(t)的节点数目Φ3(t)满足
Φ3(t)=3Φ3(t-1).
在初始条件Φ3(1)=2下,易计算知Φ3(t)=2×3t-1.
基于上述分析,一个显然的命题如下:
命题12模型N3(t)的最大独立集的数目|Ψ3(t)|为
|Ψ3(t)|=1
(27)
4 总结与问题
本文介绍了一些典型的复杂网络模型.其中,模型N1(t)被证实服从幂律度分布,模型N2(t)的度分布服从指数分布,模型N3(t)展现了等级结构.如此三个模型从不同视角刻画了真实网络中所存在的一些普世规律,不仅可以为研究真实网络提供理论依据或启发式解释,也可以丰富图论中的图类.这里,作为图论中的研究对象,这些模型的两个主要结构参数(最多叶子生成树和最大独立集)得到了详细的讨论,尽管部分参数的解析值至此仍没有准确获得,但是所得的结果已经很明显地证实了文中所提模型之间的结构差异性,例如,即使模型N1(t)和N3(t)都服从指数等于1+ln3/ln2的幂律度分布,但它们各自的最大独立集中节点的数目却是不相同的.同时,可以断言,这两个模型所拥有的最多叶子生成树的数目也是不一样的.但是,文中所有的模型也存在一些相似性,譬如,当参数t≥2时,所有模型都仅有一个最大独立集,这就足以说明,三种不同模型构造方式的内部存在着一些紧密的关联,挖掘构造方式之间类似的潜在关系将是一个有趣的研究课题,不但可以为构造更加合理的理论模型提供依据,而且有助于拓展图自身研究的深度和广度.
值得注意的是,参数|Λ|也是最小连通控制集的数目,即若在给定图G中找到最多叶子生成树,则该生成树中的非叶子节点就构成一个最小连通控制集,反之亦成立.从网络优化的角度考虑,最小连通控制集往往会对网络结构的优化设计提供理论依据.然而,最多叶子生成树问题却是NP完全理论中的一个经典问题.基于上述的讨论,模型N1(t)和N2(t)的所有最小连通控制集的数目已经得到了,但是,模型N3(t)的最小连通控制集的数目却仍没有计算出解析值.这足以展现文中三种模型之间存在的差异性.这也就是为什么本文采用这一指标研究所提出模型结构特性的主要原因.
实际上,图论是一个研究复杂网络的强有力工具,不仅可以为当前网络中的一些研究问题提供理论依据,帮助人们更合理地认识网络自身的拓扑结构,而且可以为未来网络研究的发展提供新的视角,开发新的研究方向:①基于网络结构的优化问题,确定网络模型的最多叶子生成树数目(最小连通控制集的数目),特别是为展现某些普世拓扑性质的网络模型建立有效算法去解决这一问题;②寻找唯一最大独立集的图的结构,为稀疏图的Hamilton性提供近似手段;③研究网络模型的最多叶子生成树中节点的划分问题,尤其是挖掘那些始终属于任何一棵最多叶子生成树的节点,至少可以从一个层面反映出这部分节点在网络中的重要性,为设计有效的网络控制方案提供科学指导.反过来,复杂网络如火如荼的研究发展也正在影响着当前图论的研究,为其注入了新的活力.可以相信,在未来的研究中,两者之间的结合程度会变得更加紧密,相辅相成,共同发展.
