图在约束条件下的邻点可区别全染色
2020-08-04崔福祥叶宏波
崔福祥, 杨 超, 叶宏波
(上海工程技术大学 数理与统计学院, 上海 201620)
0 引 言
图染色理论在物理、化学、计算机科学、网络理论、社会科学等领域有着广泛的应用, 具体涉及安排问题、时间表问题和计算机寄存器分配问题等. 图的可区别染色问题来源于频率分配问题, 该问题产生于移动通讯的迅速发展, 客户急剧增加, 导致用户数量不断增长与通讯网络资源有限扩容二者之间的矛盾日益突出,在此背景驱动下, 图的可区别染色问题已成为当前国内外学者研究的热点.Vizing[1]和 Behzad[2]分别于1964和1965年独立地给出了全染色的定义,并提出了点可区别全染色猜想: 任意图的点可区别全色数不超过Δ+2.随着研究的不断深化, Zhang等[3]对点可区别全染色进行弱化, 定义了图的邻点可区别全染色概念, 同时给出了邻点可区别全染色猜想: 任意图的邻点可区别全色数不超过Δ+3.目前,这两个猜想均未被解决,也没有发现这些猜想的反例. 为了更深入地研究图的可区别染色问题, 本文提出了(3)-邻点可区别全染色((3)-AVDTC) 概念,这个概念极大丰富了文献[1-6] 中的研究内容, 考虑的问题较以前更为全面, 为图染色在其他领域中的应用奠定了理论基础. 在介绍主要工作之前, 先介绍与本文相关的一些概念.
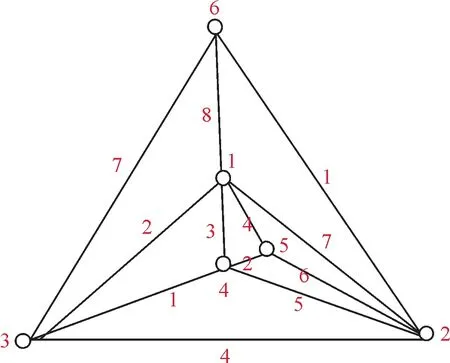
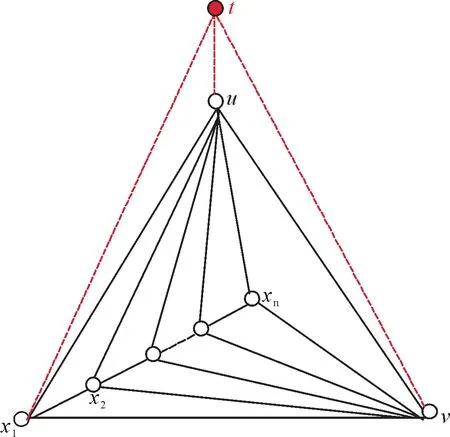
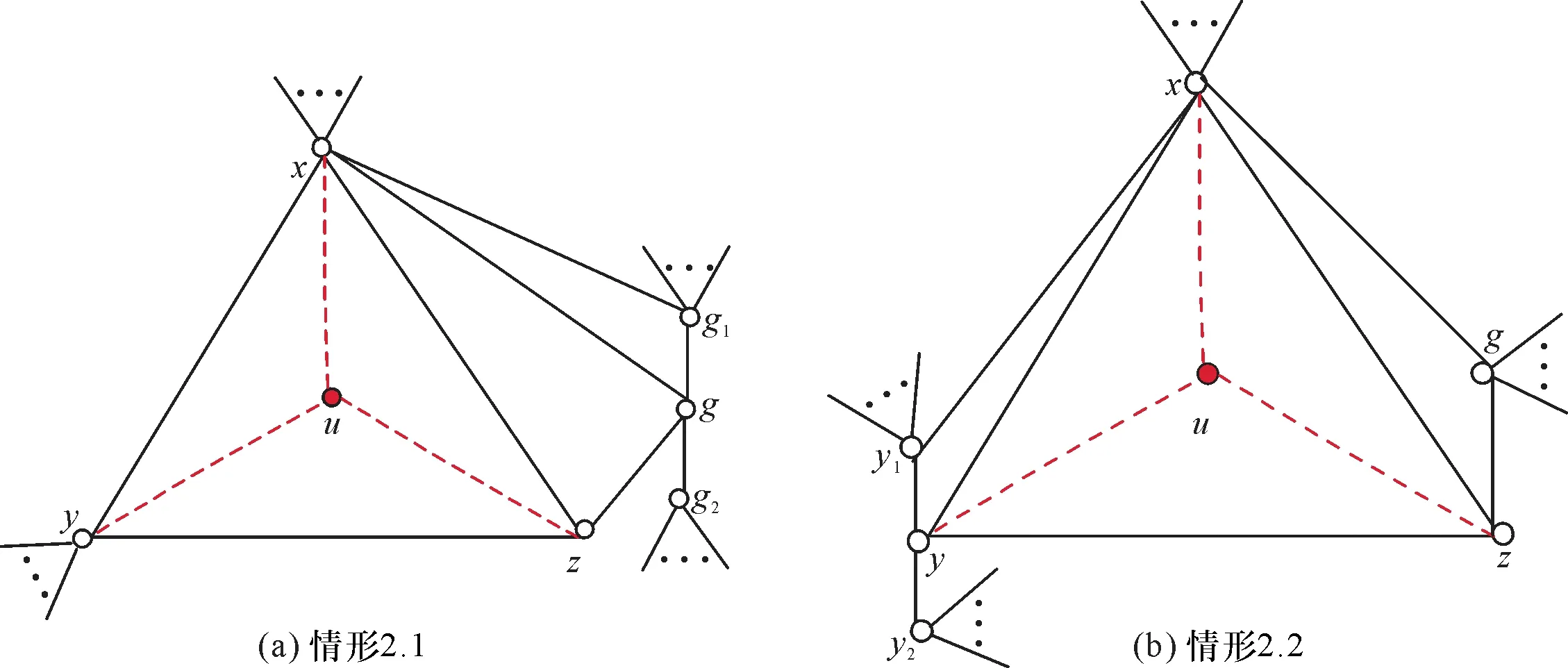
文中论及的图均为无向简单图, 且没有定义的术语和符号均采用于文献[7].符号[s,t] 表示非负整数集{s,s+1,s+2,…,t}, 其中,s和t均为整数, 且满足0≤s 定义1设f:V(G)∪E(G)→{1,2,…,k} 是图G的一个正常k-全染色.对任意的边xy∈E(G), 如果有C[f;x]≠C[f;y] 成立, 则称f是图G的一个k-(3)-邻点可区别全染色(简记为 (3)-AVDTC). 图G的(3)-邻点可区别全染色中所需最少的颜色数叫做G的(3)-邻点可区别全色数, 记为″(3)as(G). 本文将对一类特殊极大平面图的(3)-邻点可区别全染色问题进行研究. 极大平面图是指每个面的边界均为三角形, 也称为三角剖分图. 由于著名的四色定理、唯一4-可着色平面图猜想等的研究对象均与极大平面图有关联, 所以极大平面图一直都是专家学者们研究的重点对象, 他们从诸如度序列、构造、着色、可遍历性和生成运算等多方面对极大平面图相关问题展开了研究[8-9]. 定义2[10]从平面图K4出发, 逐次实施扩3-轮运算而得到的极大平面图称为递归极大平面图. 一个递归极大平面图G称为(2,2)-递归极大平面图, 如果G中恰好有2 个度数为3 的顶点, 并且这两个3 度顶点之间的距离为2. 进一步, 如果图G有2 个3 度顶点所在长度为2 路中的3 个顶点存在一个公共的相邻顶点, 则称图G为相邻型, 否则称为非相邻型. 容易证明5-阶(2,2)-递归极大平面图只有1 个, 如图 1 所示,6-阶(2,2)-递归极大平面图也只有1 个, 如图 2 所示. 图1 5-阶(2,2)-递归极大平面图Fig.1 (2,2)-recursive maximal planar graph on 5 vertices 图2 6-阶(2,2)-递归极大平面图Fig.2 (2,2)-recursive maximal planar graph on 6 vertices 引理1[10]设G是一个n阶递归极大平面图, 则G至少含有2 个3 度顶点, 并且当n≥5时, 任意两个3 度顶点之间均不相邻. 引理2[10](1)不存在恰有2个相邻的3度顶点的极大平面图; (2)不存在恰有3个两两相邻的3度顶点的极大平面图. 引理3[10](1)设G是一个阶数大于等于6 的(2,2)-递归极大平面图, 则对G中每个3 度顶点v,其邻域N(v) 中恰有一个顶点的度数为4; (2)每个不相邻型n(≥5)-阶(2,2)-递归极大平面图G有且只有一个度数为n-1 的顶点, 称此顶点为图G的中心顶点. 定理1设G是一个简单图且G中存在相邻的Δ-顶点,则″(3)as(G)≥Δ(G)+2. 证明反证法. 假设″(3)as(G)≤Δ(G)+1. 因为″(3)as(G)≥Δ(G)+1,所以″(3)as(G)=Δ(G)+1. 设uv∈E(G) 且dG(u)=dG(v)=Δ(G), 用Δ(G)+1种颜色无论怎么染色必有C2[f,u]=C2[f,v], 得矛盾.因此,″(3)as(G)≥Δ(G)+2. 将图G中的每个顶点与图H中的每个顶点之间用边连接, 得到的新图称为图G与图H的联图, 记为GH.下面给出联图P2Pn的(3)-邻点可区别全色数. 定理2″(3)as(P2Pn)=Δ(P2Pn)+2. 证明设两条路P2=uv,Pn=x1x2…xn. 令H=P2Pn. 由联图的定义知,dH(u)=dH(v)=Δ(H),dH(x1)=dH(xn)=3,dH(xi)=4,i∈[2,n-1].由定理1 知,″(3)as(H)≥Δ(H)+2. 为证″(3)as(H)=Δ(H)+2, 下面仅需证″(3)as(H)≤Δ(H)+2. 为此只需给出H的一个(Δ+2)-(3)-AVDTC 即可. 定义H的一个全染色f如下:f(u)=1,f(v)=2,f(x1)=n+1,f(x2)=n,f(xi)=i,i∈[3,n],f(uv)=n+3,f(uxi)=i+1,i∈[1,n],f(vx1)=n+2,f(vx2)=n+1,f(vxi)=n+3-f(xi),i∈[3,n],f(x1x2)=n-1,f(xixi+1)=i-1,i∈[2,n-1]. 因为dH(u)=dH(v)=Δ(H),dH(x1)=dH(xn)=3,dH(xi)=4,i∈[2,n-1],所以C(f,u)≠C(f,xi),C[f,u]≠C[f,xi],C2[f,u]≠C2[f,xi],i∈[1,n];C(f,v)≠C(f,xi),C[f,v]≠C[f,xi],C2[f,v]≠C2[f,xi],i∈[1,n];C(f,x1)≠C(f,x2),C[f,x1]≠C[f,x2];C(f,xn-1)≠C(f,xn),C[f,xn-1]≠C[f,xn].对如此构造的全染色f, 因为n+2∈{C(f,u),C[f,u],C2[f,u]},n+2{C(f,v),C[f,v],C2[f,v]}, 所以C(f,u)≠C(f,v),C[f,u]≠C[f,v],C2[f,u]≠C2[f,v]. 因为C(f,x1)={2,n-1,n+2},C(f,x2)={1,3,n-1,n+1},C(f,xi)={i-2,i-1,i+1,n-i-3},i∈[3,n-1],C(f,xn)={3,n-2,n+1};C[f,x1]={2,n-1,n+1,n+2},C[f,x2]={1,3,n-1,n,n+1},C[f,xi]={i-2,i-1,i,i+1,n-i-3},i∈[3,n-1],C[f,xn]={3,n-2,n,n+1};C2[f,x1]={1,2,n-1,n,n+1,n+2},C2[f,xi]=C[f,xi]∪{1,2},i∈[2,n].所以C2[f,x1]≠C2[f,x2],C(f,xi)≠C(f,xi+1),C[f,xi]≠C[f,xi+1],C2[f,xi]≠C2[f,xi+1],i∈[2,n-2],C2[f,xn-1]≠C2[f,xn]. 综上, 全染色f是H的一个(n+3)-(3)-AVDTC. 因此,有″(3)as(H)=n+3=Δ(H)+2. 定理3若G是一个n-阶(2,2)-递归极大平面图, 则″(3)as(G)=Δ(G)+3. 证明数学归纳法. 当n=5, 6 时, 它们的一个(Δ+3)-(3)-AVDTC 分别如图1 和图2 所示.下面考虑n-阶(2,2)-递归极大平面图在n≥7 时的(3)-AVDTC. 情形1G是相邻型的, 如图3所示. 图3 相邻型的图GFig.3 Graph G with an adjacent type 设P2=uv,Pn=x1x2…xn. 图G=V(G)∪E(G),V(G)=V(P2Pn)∪{t},E(G)=E(P2Pn)∪{tx1,tu,tv}. 由定理2 知″(3)as(P2Pn)=Δ(P2Pn)+2. 当n=5,6 时,″(3)as(G)=Δ(G)+3. 当n≥7 时,″(3)as(G)≥Δ(G)+3. 下面仅需给出G的一个(Δ+3)-(3)-AVDTC 即可.P2Pn的顶点和边保持定理2 中的染色f不变.设f*为G的一个全染色, 定义f*的一个全染色如下:f*(tx1)=Δ+2,f*(tu)=Δ+3,f*(tv)=1,f*(u)∈[1,Δ+2]{f(x1),f(u),f(v),1,Δ+2},f*(m)=f(m),m∈V(P2Pn)∪E(P2Pn). 下面分析相邻顶点色集合之间的关系. 因为Δ+3∈{C(f*,t),C[f*,t],C2[f*,t]},Δ+3{C(f*,x1),C[f*,x1],C2[f*,x1],C(f*,v),C[f*,v],C2[f*,v]}, 所以C(f*,t)≠C(f*,x1),C[f*,t]≠C[f*,x1],C2[f*,t]≠C2[f*,x1],C(f*,t)≠C(f*,v),C[f*,t]≠C[f*,v],C2[f*,t]≠C2[f*,v]. 因为dG(t)=3,dG(u)=Δ(G), 所以C(f*,t)≠C(f*,u),C[f*,t]≠C[f*,u],C2[f*,t]≠C2[f*,u]. 设pq∈V(P2Pn),则有C(f*,p)≠C(f*,q),C[f*,p]≠C[f*,q],C2[f*,p]≠C2[f*,q]. 综上,f*是图G的一个(Δ+3)-(3)-AVDTC. 故″(3)as(G)=Δ(G)+3. 情形2G是非相邻型的. 假设对n-阶(2,2)-递归极大平面图G有″(3)as(G)=Δ(G)+3 成立.设f是图G的一个(Δ+3)-(3)-AVDTC. 考察顶点数为n+1 的情况,设G*是一个n+1-阶(2,2)-递归极大平面图,G*=G+u,dG*(u)=3,N(u)={x,y.z},g∈N(z). 不妨设x为中心顶点, 由引理3, 不失一般性,设dG(z)=3. 下面分两种情况对图G的结构进行讨论. 情形2.1dG(x)=n-1,dG(y)≥5,dG(z)=3,dG(g)=4, 如图4(a)所示. 对于图G*,dG*(x)=n,dG*(y)≥6,dG*(z)=4,dG*(g)=4,dG*(u)=3. 设是图G*的一个全染色, 定义如下:(uz)∈[1,Δ+3]C2[f,g]∪{f(xz),f(yz)},(uy)∈C2[f,y]C[f,y]∪{(uz)},(ux)∈C2[f,x]C[f,x]∪{(uy),(uz)},(u)∈C2[f,y]{(ux),(uy),(uz),f(x),f(y),f(z)},(t)=f(t),t∈V(G*)∪E(G*){ux,uy,uz,u}.因为dG*(u) 情形2.2dG(x)=n-1,dG(y)=4,dG(z)=3,dG(g)≥5, 如图4(b)所示. 图4 情形2.1和情形2.2 的结构示意图Fig.4 Structure of Case 2.1 and Case 2.2 对于图G*,dG*(x)=n,dG*(y)=5,dG*(z)=4,dG*(g)≥5,dG*(u)=3. 设ρ是图G*的一个全染色, 定义ρ如下:ρ(uz)∈[1,Δ+3]C2[f,g]∪{f(xz),f(yz)},ρ(uy)∈C2[f,y]C[f,y]∪{ρ(uz)},ρ(ux)∈[1,Δ+3]C[f,x]∪C2[f,y]∪{ρ(uy),ρ(uz)},ρ(u)∈C2[f,y]{ρ(ux),ρ(uy),ρ(uz),f(x),f(y),f(z)},ρ(t)=f(t),t∈V(G*)∪E(G*){ux,uy,uz,u}.因为dG*(u) 基于情形1和2, 本定理得证. □ 极大平面图由于其特殊的结构使得它在数学和计算机科学领域被广泛研究, 尤其在四色定理的研究中发挥着极其重要的作用.本文仅对一类极大平面图的(3)-邻点可区别全染色进行了研究, 希望感兴趣的读者在更多极大平面图的(3)-邻点可区别全染色问题上贡献力量. 图的(3)-邻点可区别全染色是邻点可区别全染色的一个推广, 受Zhang等在文献[3]的邻点可区别全染色猜想的启发, 本文进一步提出图的(3)-邻点可区别全染色猜想: 猜想若图G是一个简单图, 则″(3)as(G)≤Δ(G)+3.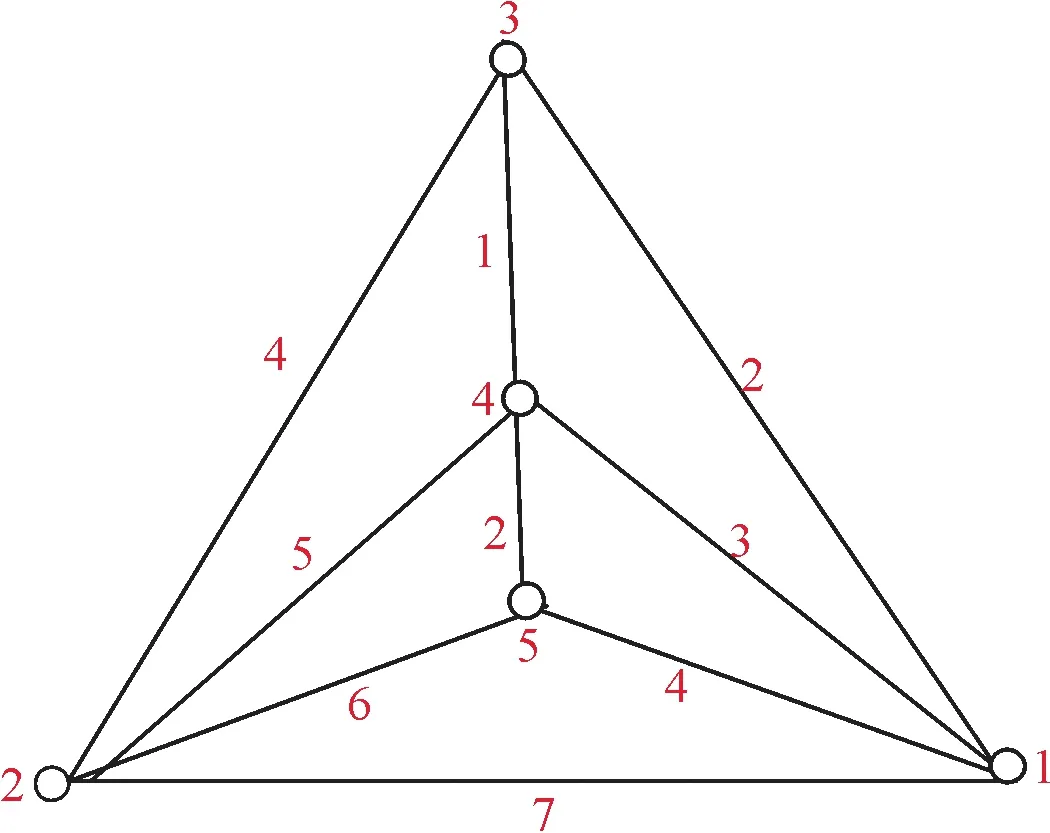
1 主要结果及证明
2 讨 论
