悬浮Ar-CH4纳米液滴蒸发过程的分子动力学模拟
2020-08-04王宝和侯兆泷
王宝和,侯兆泷,王 维
(1.大连理工大学 化工学院,辽宁 大连 116024;2.大连理工大学 化工机械与安全学院,辽宁 大连 116024)
多组分混合物液滴的蒸发广泛应用于工业生产中,燃料的雾化、生产过程中的喷雾冷却及蒸发等都涉及双组分甚至多组分的液滴蒸发[1]。与单一组分液滴的蒸发过程相比,多组分混合物液滴的蒸发要复杂得多。由于不同组分的挥发性存在差异,导致多组分混合物液滴的组成随着时间不断变化,增大了研究的难度[2]。到目前为止,对于纯组分悬浮液滴及多组分混合物液滴的蒸发,主要集中在微米及其以上尺度液滴的实验、理论及计算机模拟等研究方面,已经取得了一些丰硕成果[3]。对于纳米级悬浮液滴而言,其蒸发特性的实验测试还是比较困难。近年来,随着计算机技术的迅猛发展,以及分子动力学(MD)模拟技术的出现,对纯组分悬浮纳米液滴的蒸发过程取得了一些研究进展,但对于多组分混合物悬浮纳米液滴蒸发过程的分子动力学模拟研究报道很少[4-5]。本文拟采用分子动力学模拟方法,利用LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)软件,探讨模拟温度、液滴初始直径、甲烷摩尔分数及惰性组分对Ar-CH4混合物悬浮纳米液滴蒸发行为的影响[6]。
1 模拟方法
1.1 模拟体系
模拟体系的初始模型如图1所示。采用直角坐标系,球形液滴的质心位于立方体模拟盒子的中心。模拟盒子在x、y、z三个方向上长度分别为Lx=Ly=Lz=L。初始时刻,一定数量饱和液体氩和甲烷的混合物随机分布成球形液滴,两种组分完全混合。甲烷分子采用联合原子模型。初始速度由随机数发生器确定[7]。为了减少达到平衡所用的时间,在气体空间内填充饱和气体氩分子和甲烷分子。

图1 初始模型
1.2 模拟细节
模拟在x、y、z三个方向均采用周期性边界条件,截断半径为1.6 nm。系统采用正则系综(NVT),采用Woodcock变标度恒温法,实现系统恒温。时间步长取0.5 fs,不断进行质心校正,使质心处于模拟盒子的中心。经过2 ns进行平衡分子动力学模拟,得到相关模拟参数,再经过8 ns进行非平衡分子动力学模拟,探究各种因素对液滴蒸发行为的影响规律。
1.3 势能函数
甲烷是一种正四面体结构的非极性分子。本文将甲烷分子看作一个刚性整体,采用如图2所示的联合原子模型。
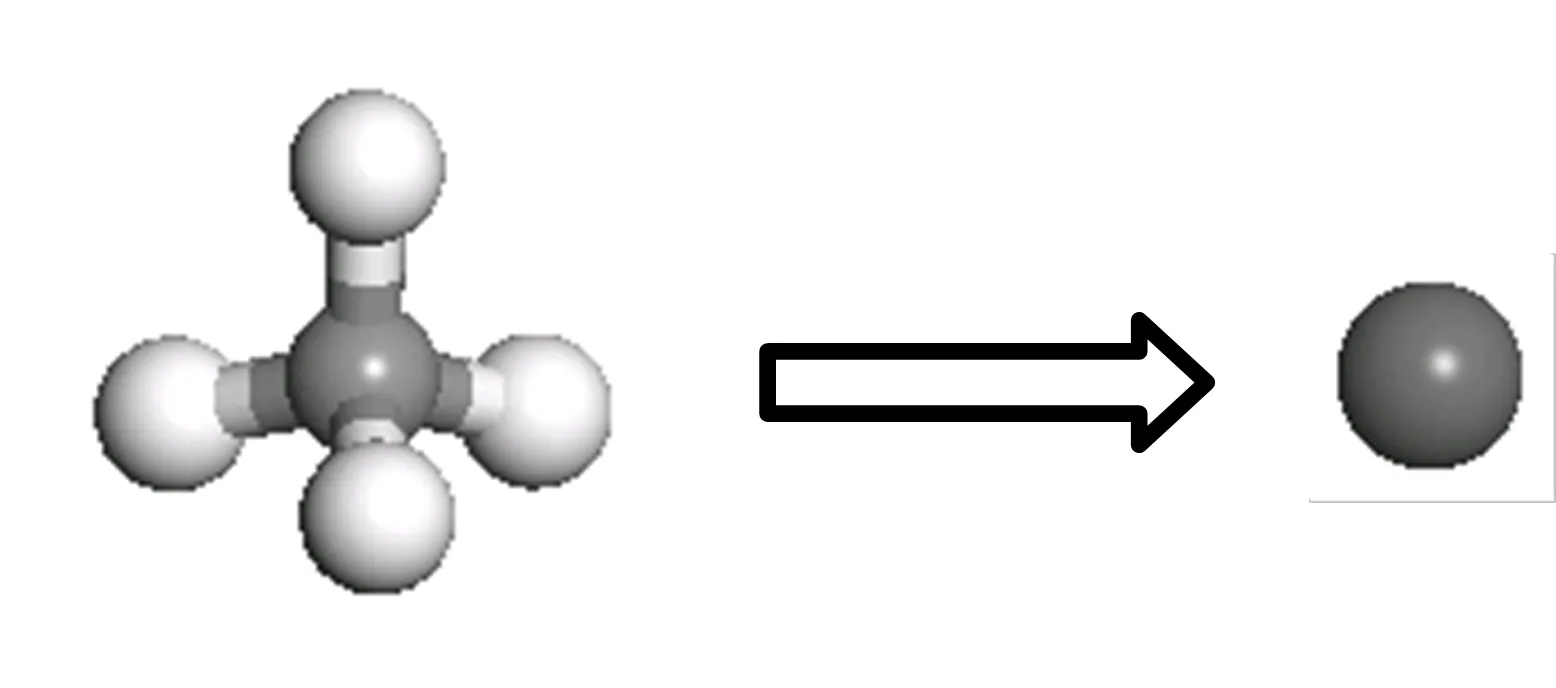
图2 甲烷的联合原子模型示意图
在本研究的分子动力学模拟中,对于氩分子之间或甲烷分子之间的作用势,采用Lennard-Jones(L-J)势能函数,如方程(1)所示[8]。
(1)
其中:U为势能函数;rij为分子i和j之间的距离;ε为能量参数;σ为长度参数。如表1所示[9]。

表1 势能参数
对于氩分子与甲烷分子之间的作用势能,依然采用L-J势能函数,如方程(2)所示[8]。
(2)
其中:rAC为氩分子与甲烷分子之间的距离;σAC为氩分子与甲烷分子之间的长度参数;εAC为氩分子与甲烷分子之间的能量参数。对于不同种类的原子之间的能量参数和长度参数,可由Lorentz-Berthelot混合规则进行计算,如方程(3)和(4)所示[8]。
σAC=(σA+σC)/2
(3)
(4)
其中:σA为氩分子间的长度参数;σC为甲烷分子间的长度参数;εA为氩分子间的能量参数;εC为甲烷分子间的能量参数。
1.4 液相分子数及纳米液滴球形度的确定
Amsterdam规则认为,如果在距离i分子的Rij范围内,至少存在4个j分子,就可以认为,分子i是液相中的分子[10]。其中Rij为分子i和j之间的距离,Rij一般取1.542σ。
对于悬浮混合物纳米液滴的球形度S,其定义如式(5)所示[11]。
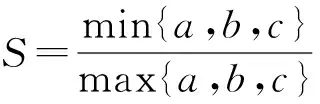
(5)
其中:a、b、c分别是球形混合物纳米液滴在坐标轴x、y、z三个方向上的长度,这3个参数可根据LAMMPS软件输出的密度文件得到[11]。
1.5 纳米液滴半径及蒸发速率的确定
假设悬浮混合物纳米液滴在蒸发过程中,始终保持规则的球形不变。则纳米液滴的半径R,就可以根据液相中氩分子数和甲烷分子数,由方程(6)计算得到。
(6)
其中:R为球形纳米液滴的半径;NLA为氩分子数;NLC为甲烷分子数;mA为一个氩分子的相对分子质量,mA=6.636×10-26kg;mC为一个甲烷相对分子质量,mC=2.622×10-26kg;ρL为液相主体的平均密度。
对于Ar-CH4二元混合物纳米液滴而言,蒸发速率是指单位时间内、单位面积上蒸发出来的氩分子和甲烷分子的总质量,即为氩蒸发速率和甲烷蒸发速率的总和,又称总蒸发速率。本文通过非平衡分子动力学模拟,可以得到液相中氩分子数和甲烷分子数随时间变化的拟合曲线及其曲线的斜率,再利用方程(7),就可以得到悬浮混合物纳米液滴的蒸发速率。
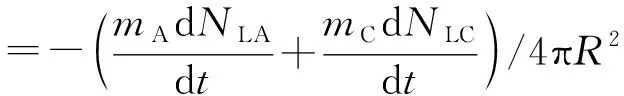
(7)
其中:v是蒸发速率,kA为氩分子数随时间变化拟合曲线的斜率,kA=dNLA/dt;kC为甲烷分子数随时间变化拟合曲线的斜率,kC=dNLC/dt;A为液滴的表面积,t为时间。
2 结果与讨论
采用增大模拟盒子体积的方法,来实现非平衡分子动力学模拟。初始模拟盒子边长为13 nm,初始体积为V0。当系统达到平衡时,模拟盒子的6个方向扩大相同距离,使体积增量达到1.57V0[12]。采用非平衡分子动力学模拟的方法,探讨Ar-CH4二元混合物体系的模拟温度、液滴初始直径、甲烷摩尔分数及惰性组分对纳米液滴球形度和蒸发速率的影响规律。
2.1 温度的影响
对于4 200个氩分子和1 800个甲烷分子组成的混合物球形纳米液滴,相应的甲烷摩尔分数0.3。采用非平衡分子动力学模拟,得到不同温度下,Ar-CH4二元混合物悬浮纳米液滴的球形度随时间的变化及蒸发速率曲线,分别如图3和图4所示。

图3 不同温度下混合物纳米液滴的球形度随时间的变化
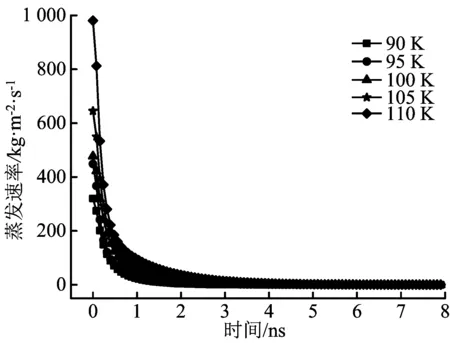
图4 不同温度下混合物纳米液滴的蒸发速率曲线
由图3可见,当蒸发过程开始时,由于模拟盒子内部的实际气相密度分布并不均匀,液滴在汽-液界面处不对称性蒸发,导致纳米液滴的球形度迅速减小;之后,纳米液滴球形度维持在一定的数值上波动。在整个蒸发过程中,纳米液滴基本为球形;且模拟体系温度越高,球形度越小,这与CONSOLINI等[5]的研究结果基本一致。
由图4可见,在蒸发过程的初期,混合物纳米液滴的蒸发速率比较大,而且模拟温度越高,蒸发速率越大;随着蒸发时间的延长,蒸发速率先急剧减小,然后,再缓慢减小。
2.2 液滴初始直径的影响
在甲烷的摩尔分数为0.3,模拟温度为100 K的条件下,采用非平衡分子动力学模拟方法,得到不同初始直径下,悬浮混合物纳米液滴的球形度变化及蒸发速率曲线,分别如图5和图6所示。
由图5可知,当蒸发过程开始时,混合物纳米液滴的球形度迅速减小;之后,维持在一定的球形度数值上波动。在整个蒸发过程中,纳米液滴基本为球形;纳米液滴的初始直径越大,球形度越大,与文献[8]得到的结果基本相同。
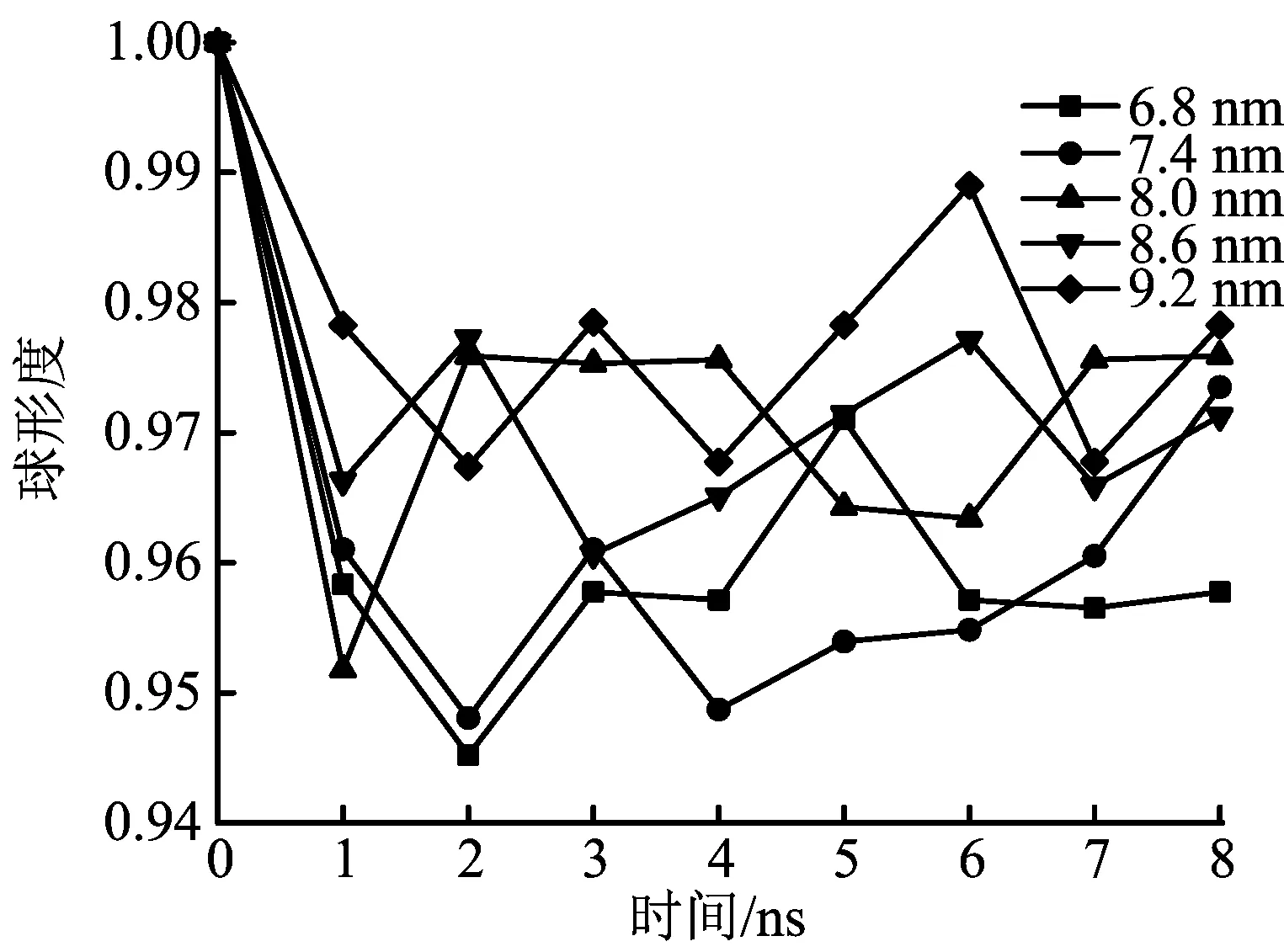
图5 初始直径对悬浮混合物液滴球形度的影响
由图6可见,在蒸发过程的初期,不同初始直径下混合物纳米液滴的蒸发速率都比较大,而且初始直径越小,液滴蒸发速率越快,这与CRAFTON等[13]得到的结果基本一致。
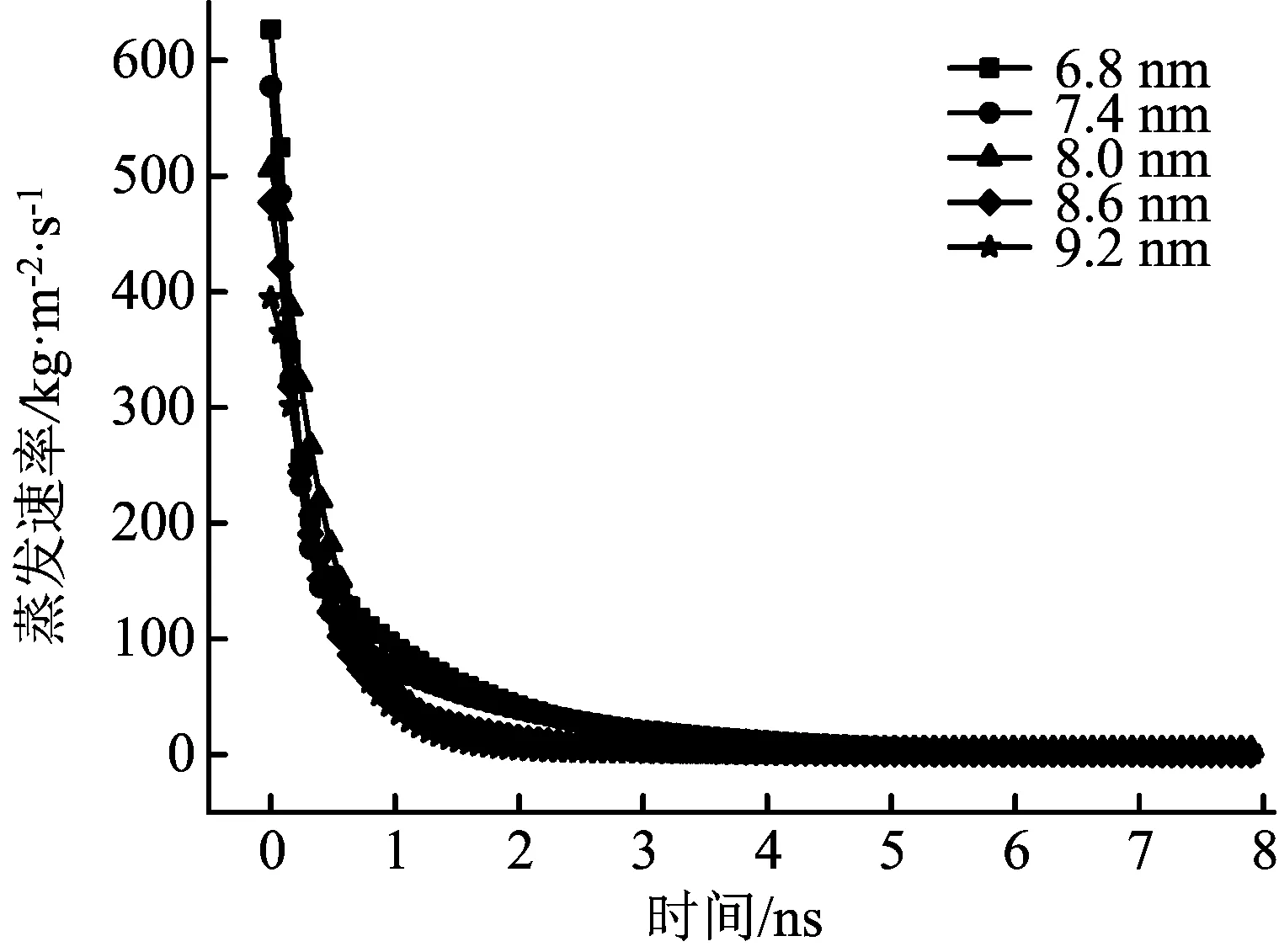
图6 初始直径对悬浮混合物纳米液滴蒸发速率的影响
2.3 甲烷摩尔分数的影响
在模拟体系温度为100 K,初始直径为8.4 nm的条件下,采用非平衡分子动力学模拟方法,得到不同甲烷摩尔分数下,悬浮混合物纳米液滴的球形度随时间的变化及蒸发速率曲线,分别见图7、图8。

图7 甲烷摩尔分数对混合物悬浮纳米液滴球形度的影响
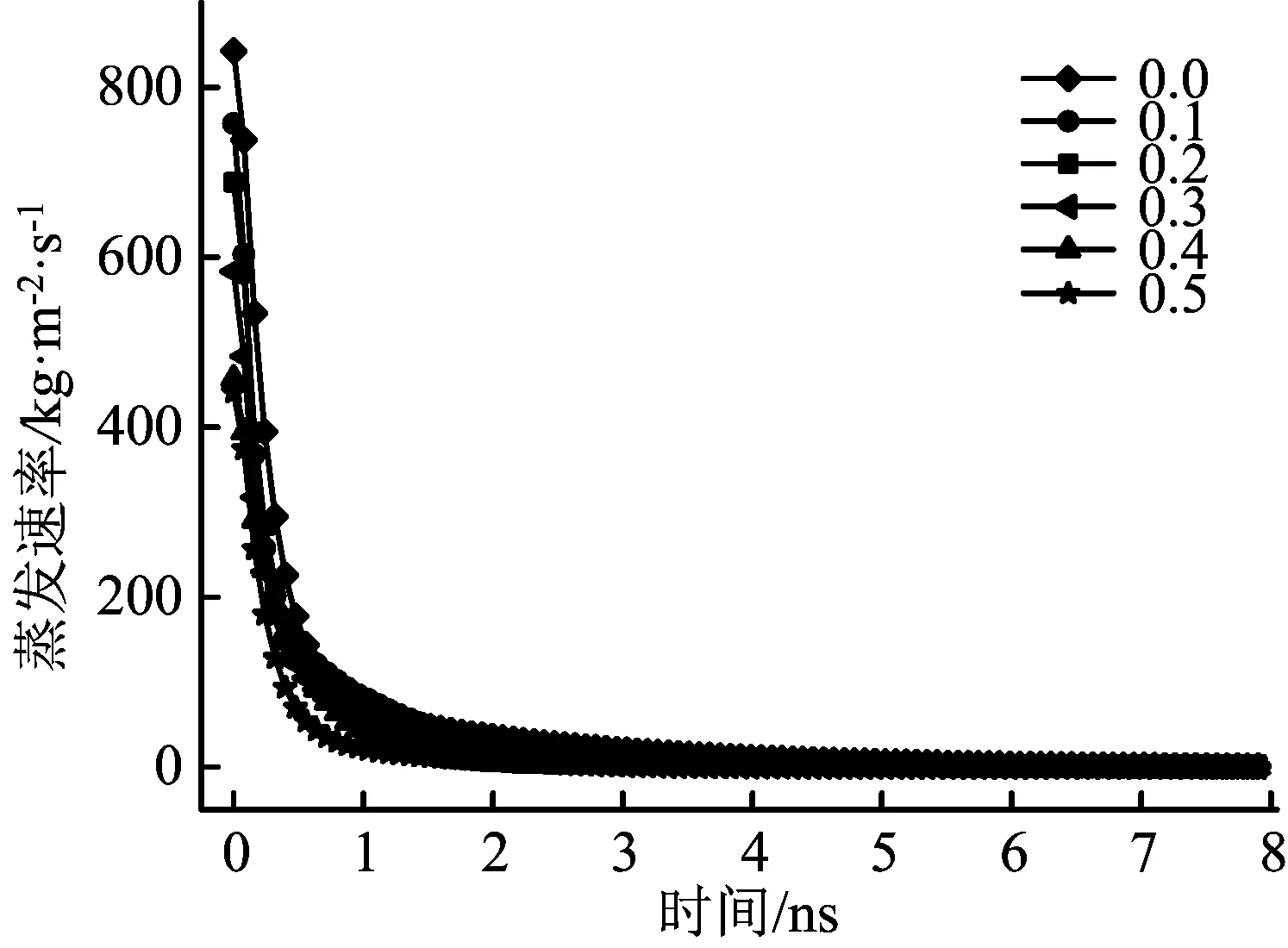
图8 甲烷摩尔分数对混合物悬浮纳米液滴蒸发速率的影响
甲烷的摩尔分数对液滴总蒸发速率的影响如图7所示。可以看出,当蒸发过程开始时,混合物纳米液滴的球形度迅速减小;之后,维持在一定的球形度数值上波动。在整个蒸发过程中,纳米液滴基本为球形;甲烷的摩尔分数对球形度的影响不大。
由图8可知,在蒸发过程的初期,不同甲烷摩尔分数下的纳米液滴蒸发速率均小于纯氩纳米液滴;而且甲烷摩尔分数越大,其蒸发速率越小。
2.4 惰性组分的影响
在模拟温度为100 K,甲烷摩尔分数为0.3,液滴初始直径相同时,分别在气体空间中填充0、50、100、150、200个氮气分子,进行非平衡分子动力学模拟,计算得到的液滴蒸发速率,如图9所示。

图9 惰性组分对混合物悬浮纳米液滴蒸发速率曲线的影响
由图9可见,在气体空间内加入不同数量的氮气分子,混合物液滴的蒸发速率基本不变,说明在气相中加入惰性组分并不影响悬浮纳米混合物液滴的蒸发速率。
3 结论
采用非平衡分子动力学模拟方法,研究了Ar-CH4二元混合物体系的悬浮纳米液滴的蒸发行为,获得如下结论。①当蒸发过程开始时,混合物纳米液滴的球形度迅速减小;之后,维持在一定的球形度数值上波动。在整个蒸发过程中,纳米液滴基本为球形;模拟温度越高,液滴初始直径越小,球形度越小;甲烷摩尔分数对球形度的影响不大。②在蒸发过程的初期,混合物纳米液滴的蒸发速率比较大,而且模拟温度越高,液滴初始直径越小,甲烷摩尔分数越小,蒸发速率越大;随着蒸发时间的延长,蒸发速率先急剧减小,然后,再缓慢减小。③气体空间内惰性组分加入,并不影响混合物纳米液滴的蒸发速率。
