一种基于云机器人的综合管廊智能巡检调度算法

周熙炜，尚 宵，尚新娟，闫茂德，王发发

（长安大学，陕西 西安 710064）

0 引言

地下综合管廊，又称“共同沟”，担负着输送介质、能量和传输信息的功能，是城市的“生命线”。采用综合管廊的建设方式，能合理、有效地利用城市地下空间，科学地敷设各类市政管线，有利于管廊内部的运维。随着人工智能及机器人技术的不断发展，基于巡检机器人移动监测的技术方案应运而生；但受自身存储空间等因素的影响，机器人不能及时更新信息，降低了系统的实时性能，故提出使用云机器人来解决上述问题。云机器人是“机器人+物联网+云计算”技术结合的新型应用，借助云端强大的并行计算能力、存储和通信资源，可以把巡检机器人本体的数据处理、规划、决策及协作等复杂计算功能“卸载”到云平台，机器人本体仅需保留最基本的传感器、执行器和处理单元来完成一些高实时性作业，以减小机器人体积、降低功耗、延长航程，从而解决制约机器人应用的系统复杂度高、智力水平低和可靠性差等问题。

云机器人的路径规划与调度算法一直受到研究学者们的广泛关注。ASORO实验室采用Hadoop分布式系统构架，建立了云计算基础设施并生成3D环境模型，从而支持机器人进行即时定位与地图构建[1]；Arumugam R等人[2]利用Hadoop计算群和ROS系统提出了DavinCi软件框架，将云计算应用在服务机器人中；赵连翔等人[3]将云计算的理念运用到机器人遥控操作上，设计了机器人云操作平台。Kenendy博士和Eberhart博士于1995年首次提出粒子群优化算法（particle swarm optimization, PSO）[4]，该算法已被广泛应用到函数优化、神经网络训练及模糊控制系统等多个领域。文献[5-7]分别对PSO算法进行了改进，并应用其解决了复杂的非凸/非线性电力系统经济负荷分配问题、BP（back propagation）神经网络短时交通流预测和障碍环境下机器人的路径规划问题。

管廊巡检机器人在特殊管隧环境下工作，国内外的研究文献中对于管廊的巡检调度问题探究较少，但对于矿山、车间及物流等机器人调度问题的研究常见诸文献。文献[8]提出引入多智能体技术（Multi-Agent），运用GA-ANFIS（遗传算法-自适应模糊神经系统）算法并采用黑板通信模式建立智能化的露天矿山生产调度系统。文献[9]利用禁忌搜索算法来规划并解决有限等待制造单元的双小车调度线路最优解问题。魏文义等人提出的三段运行方式行车调度方案可提升车辆的运输效率、减小车辆的候车概率[10]。本文针对管廊运营瞬发量和缓发量灾害，提出了一种改进的自适应权重粒子群-遗传混合优化算法，以提高管廊内管线泄漏源检测的实时性。

1 机器人调度的数学模型

在对管廊巡检技术设计时，管廊各巡检区域将由不同的机器人不间断地往复巡检，预计每10 km管廊采用30个机器人以1～3 m/s速度巡检。正常工作时，巡检机器人在自己的区域以一定速度往复巡检；当管廊内部发生燃气泄漏或火灾等情况、需要机器人定点监测或机器人损坏时，当前机器人停在原地不动，而该机器人负责的区域需要由左右两侧临近的机器人来承担，此时我们对巡检机器人建立调度模型。

各机器人之间不可翻越，假设需要定点监测或损坏的机器人不发生在端点处，否则将有一侧成为死区而无法被监测。建立机器人调度的目标函数，即巡检一次耗时最长的机器人其巡检时间的最小值：

其约束条件如下：

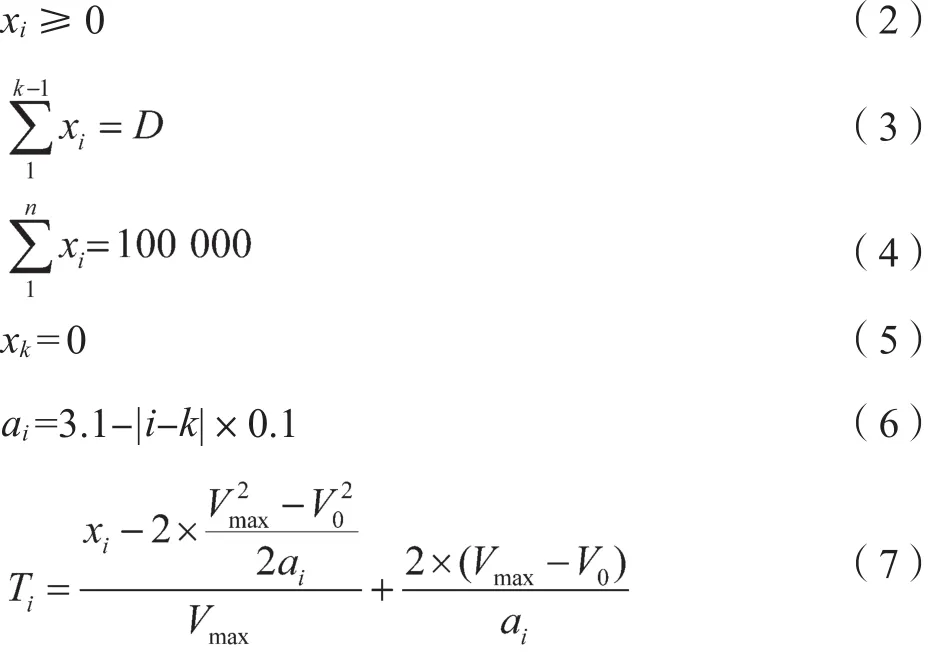
式中：n——巡检机器人的数量，本文中n=30；xi——机器人i巡检的区域长度；vi——机器人i的巡检速度；Ti——机器人i的调度时间；D——发生灾害点的机器人距离巡检最左端的距离长度（将机器人从左到右依次进行从小到大的编号）；k——灾害点机器人的标号；ai——机器人i的加速度；vmax——机器人运行的最大速度；v0——机器人在巡检区域端点处的速度。

约束条件中，式（2）是对每个机器人巡检区域长度的约束；式（3）和式（4）是灾害点到巡检总长度左端点的距离和巡检总长度；式（5）是灾害点处机器人不分配巡检区域；式（6）是机器人i的加速度，离灾害点最近的左右两个机器人加速度均为3 m/s2，两侧机器人的加速度依次递减0.1 m/s2；式（7）是重新划分巡检区域时，机器人在巡检区间里先加速、再匀速、最后减速的过程由运动学公式得到机器人i巡检一次所用的时间，在巡检区间端点处的速度均为0，匀速运动时速度为3 m/s。

2 适用的调度算法比较

在管廊巡检调度系统中，机器人通过本体携带的感知单元与RFID路标等辅助定位技术结合，与上位机进行实时信息交流；一旦检测到泄漏源，即可精确定位到灾害点处的位置信息，确定灾害点处实时监测的机器人的标号，然后重新分配该机器人左右两侧的巡检区域。管廊巡检调度系统对算法的实时性要求较高，适用的算法包括PSO算法与遗传算法（genetic algorithm，GA）。PSO算法与GA算法在种群多样性、收敛速度和全局寻优能力上有互补性，二者相结合可提高算法的整体性能。

PSO中每个粒子代表一个机器人在一段区域内的巡检长度，算法得到的优化极值为巡检一次巡检耗时最长的机器人巡检时间的最小值。有些学者提出权重会根据粒子位置的变化而动态改变的观点。根据全局最优点的距离调整算法，对PSO采用非线性动态惯性权重系数，使得算法能够自适应更新权值，惯性权重随粒子目标函数值的改变而改变，而惯性权重的改变有利于增加粒子的寻优能力。惯性权重ω的表达式如下：

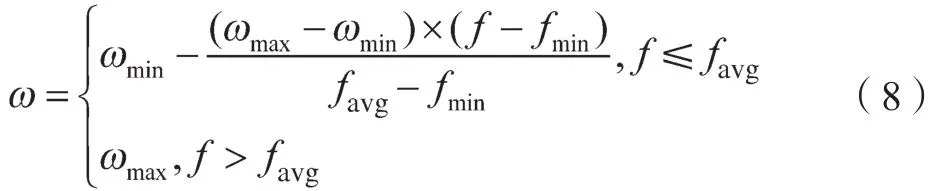
式中：f——粒子实时的目标函数值；favg——当前所有粒子平均值；fmin——当前所有粒子最小目标函数值[11]。

GA算法先初始化一个种群，按照生物进化的原理根据适应度大小挑选出好的个体，然后通过交叉、变异操作得到代表新的解集的种群。PSO算法和GA算法相同点为：两者均属于仿生类全局优化算法，在解空间内随机产生初始种群，然后在全局解空间适应性好的部分集中搜索，但是在解决高维问题时易陷入局部最优。不同之处在于：PSO算法的粒子均保存自己历史最优解信息，且粒子按照位置和速度更新公式来更新自己，具有一定方向；而GA算法会随着种群的破坏而丢失以前的信息，交叉和变异操作都是随机操作，没有确定的方向。

3 改进的调度算法

采用GA算法可有效地求解优化问题，但不论是交叉还是变异操作，都缺乏明确的导向性，因此其对空间最优解的逼近能力不强。PSO算法的速度与位置更新公式让粒子有很强的导向性，空间寻优能力很强，但容易陷入局部最优[12]。结合GA算法的极强探索精度和求变功能、在解空间全局寻优的优势[13]和PSO中粒子的强导向性，本文提出一种自适应权重的PSO算法（adaptive weight particle swarm optimization, AWPSO）和GA算法相结合的混合算法（AWPSO-GA算法）。

首先随机初始化粒子群以及粒子的初始位置和速度，计算每个粒子的适应度值。接着粒子进行AWPSO算法流程，以单次飞行得到的个体极值的1.5倍为半径，作为GA初始种群的取值范围；再通过GA的交叉、变异操作，得到经过2次筛选、拥有遗传算法最优解的粒子。最后用GA得到的最优解替换AWPSO算法中适应度最低个体，这样在一次大的迭代中可以得到具有飞行方向和遗传算法优点的适应度较高的个体，以此来增加算法寻优效率并避免某一个算法的局限性。

本文所提的AWPSO-GA算法具体步骤如下：

（1）初始化粒子种群。群体规模为N，粒子的取值范围[-xmax,xmax]，粒子的速度范围[-vmax,vmax]，最大权重为ωmax，最小权重为ωmin，最大迭代次数I，交叉概率Pc，变异概率Pm。

（2）计算各粒子适应度值。

（3）根据速度和位置公式更新粒子的速度和位置。

（4）根据式（8）更新惯性权重。

（5）用粒子适应度值和个体极值比较，将适应度值更好的更新为当前最好位置。用粒子的适应度值和全局极值比较，将适应度值更好的更新为全局最好位置。

（6）将PSO算法得到的个体作为GA的初始种群，对其进行交叉、变异操作。

（7）判断是否满足终止条件（最大迭代次数）。如果否，将得到的新粒子种群返回到步骤（2）；如果是，则输出最优解。

4 仿真分析

假设灾害点位置在7.50 km处，即在第23个巡检机器人监控区域监测到的灾害点，对其左右两侧机器人巡检区域进行异常动态分配。利用PSO，AWPSO及本文所提的AWPSO-GA算法分别进行仿真实验，得到重新划分的区间长度和机器人巡检一次耗时最长机器人巡检时间的最小值。各算法的参数设置分别如表1～表3所示，其中c1和c2为加速度常数。

表1 PSO的参数设置Tab.1 Parameter settings of PSO

表2 AWPSO的参数设置Tab.2 Parameter settings of AWPSO

表3 AWPSO-GA的参数设置Tab.3 Parameter settings of AWPSO-GA

对上述3种算法分别进行了25次仿真实验，得到以迭代次数为横坐标、函数适应值为纵坐标的寻优结果图，并用表4记录了求解巡检一次最短时间的结果。

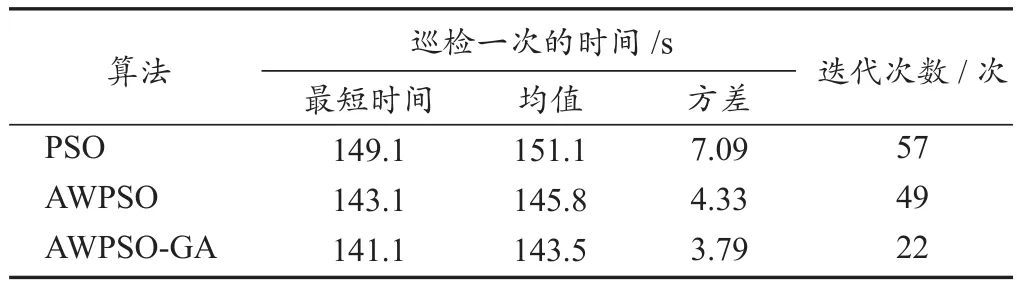
表4 3种算法结果比较Tab. 4 Results comparison of the three algorithms

图1示出PSO, AWPSO和AWPSO-GA算法寻优结果。可以发现，PSO, AWPSO和AWPSO-GA算法分别在迭代57次、49次和22次后达到最优，其中AWPSO-GA算法迭代次数最少；3种算法最优解分别为tmin=149.110 8 s，tmin=143.073 7 s，tmin=141.147 8 s。图2示出采用AWPSO-GA算法所求得的最优时间对应的小车重新分配的巡检区间长度。

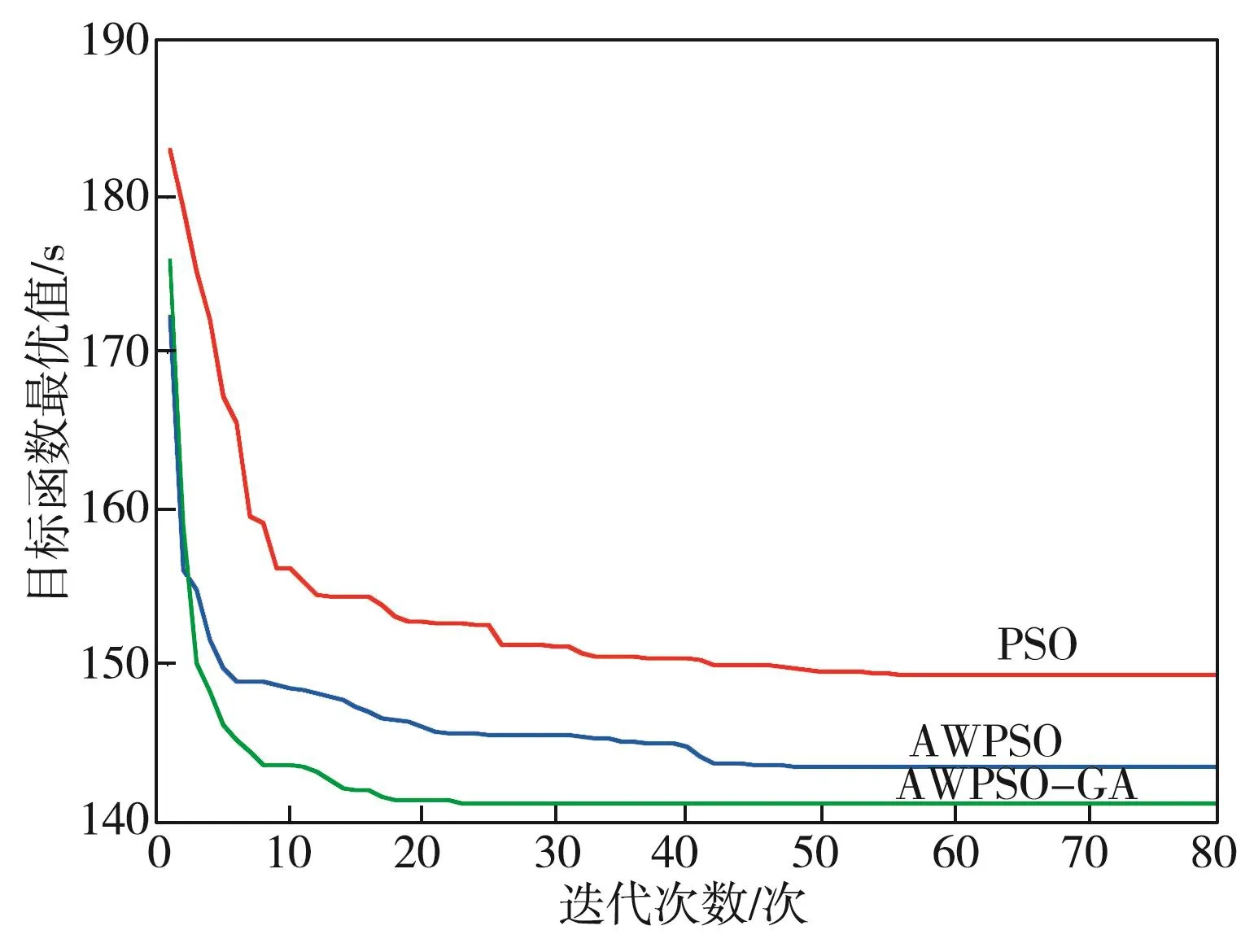
图1 3种算法寻优结果Fig. 1 Optimization results of the three algorithms

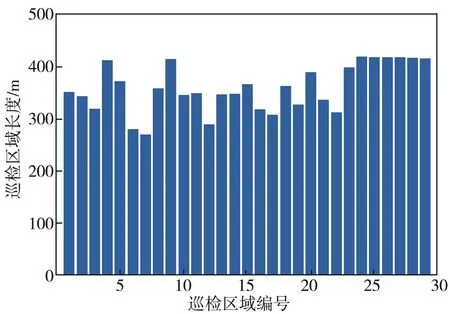
图2 机器人重分配巡检区域的长度Fig. 2 Length of the inspection area distributed by robot

通过对比寻优结果图的3条曲线可以看出：AWPSO的收敛速度稍高于PSO的，得到的巡检最小时间也相比PSO的短；相比AWPSO和PSO，AWPSOGA收敛速度更快，巡检调度所用的最小时间更短。这说明改进的混合算法对求解最小化管廊巡检机器人耗时最长的巡检时间问题更有效。

5 结语

本文以城市地下管廊巡检的机器人调度耗时最长的时间最小化为目标函数，采用PSO，AWPSO和AWPSO-GA算法分别对模型进行了优化求解。仿真结果表明，本文提出的AWPSO-GA算法寻优效果更好、迭代次数少，满足巡检调度实时性的要求。目前，国内外云机器人在地下综合管廊中的应用研究尚处空白，本文所建立的调度模型立足于实践、可行性强，其研究工作对地下管廊的运营和维护有着重要的意义。对于管廊巡检中存在的各种非线性因素，如机器人定位精度、传感器灵敏度和误报率等，会对系统的运维带来扰动，本文后续将开展更多的研究工作。