基于双目结构光的高铁白车身三维测量方法

张海洋 ，陈 巍 ，叶松涛 ，陈新宇

（1. 华中科技大学 无锡研究院，江苏 无锡 214000；2. 无锡中车时代智能装备有限公司，江苏 无锡 214000）

0 引言

高铁白车身是指未经涂装的高速列车车身。目前国内外围绕高铁白车身的自动化生产展开了大量的研究，其中的研究热点是将工业机器人技术应用于高铁列车腻子打磨，以提升加工效率。机器人腻子打磨一般需要根据加工对象三维模型进行路径规划，因此需要引入相应的测量方法来实现高铁白车身表面三维模型的测量；此外，白车身腻子表面打磨完成后，还需要通过测量其表面平整度对打磨质量进行评价，而采用合适的测量方法有利于提高检测效率，降低检测误差。

高铁白车身属于大型工件，国内外针对大型工件的三维测量取得了不错的技术成果。其中三坐标测量技术属于接触式测量方式，测量时将测头与物体接触，然后通过移动导轨来实现物体测量，该方法测量精度高、可靠性好，但是测量效率低、对环境要求高，无法实时跟踪测量。编码结构光技术是通过在两幅图像上找到同名点再基于三角法来进行三维重建，并额外采用一个投影仪投射编码图案到被测物体表面对其进行编码，对编码信息解码后再进行后续的测量。该方式适用于表面特征和纹理不明显物体的三维形貌测量。虽然三维测量方式经历了长期的研究发展，但对于不同对象的不同因素，其仍旧具有较为广阔的研究空间[1-4]。

本文引入一种基于编码结构光（面结构光）的三维测量技术，以实现高铁白车身腻子机器人打磨的“测量-加工”作业一体化；除此之外，本文还提出了基于“极线斜率-相位”查找容器的快速匹配方法与基于多球面特征的点云粗拼接技术，以提高点云匹配速度与精度，有效解决了具有低重叠区域的两块点云拼接困难的问题。

1 双目结构光三维测量技术

使用双目结构光进行三维测量的原理是，通过投影仪将一系列编码图案投影至待测物体表面，再由左右相机拍摄在物体表面发生畸变的条纹图像（条纹的畸变包含了物体表面的三维信息）；然后根据相关解码与匹配算法获得左右相机像素点的映射关系，再利用三角测量方法获取物体像素对应的三维点信息。双目结构光原理如图1所示，其中oc1xc1yc1zc1和oc2xc2yc2zc2分别表示左右相机的坐标系，o1u1v1与o2u2v2则分别表示左右相机图像坐标系，被测物体上的P点分别对应左右相机上的 p1与p2像素点。利用 p1与p2像素点坐标与相机标定参数，即可求出空间点P的三维坐标。

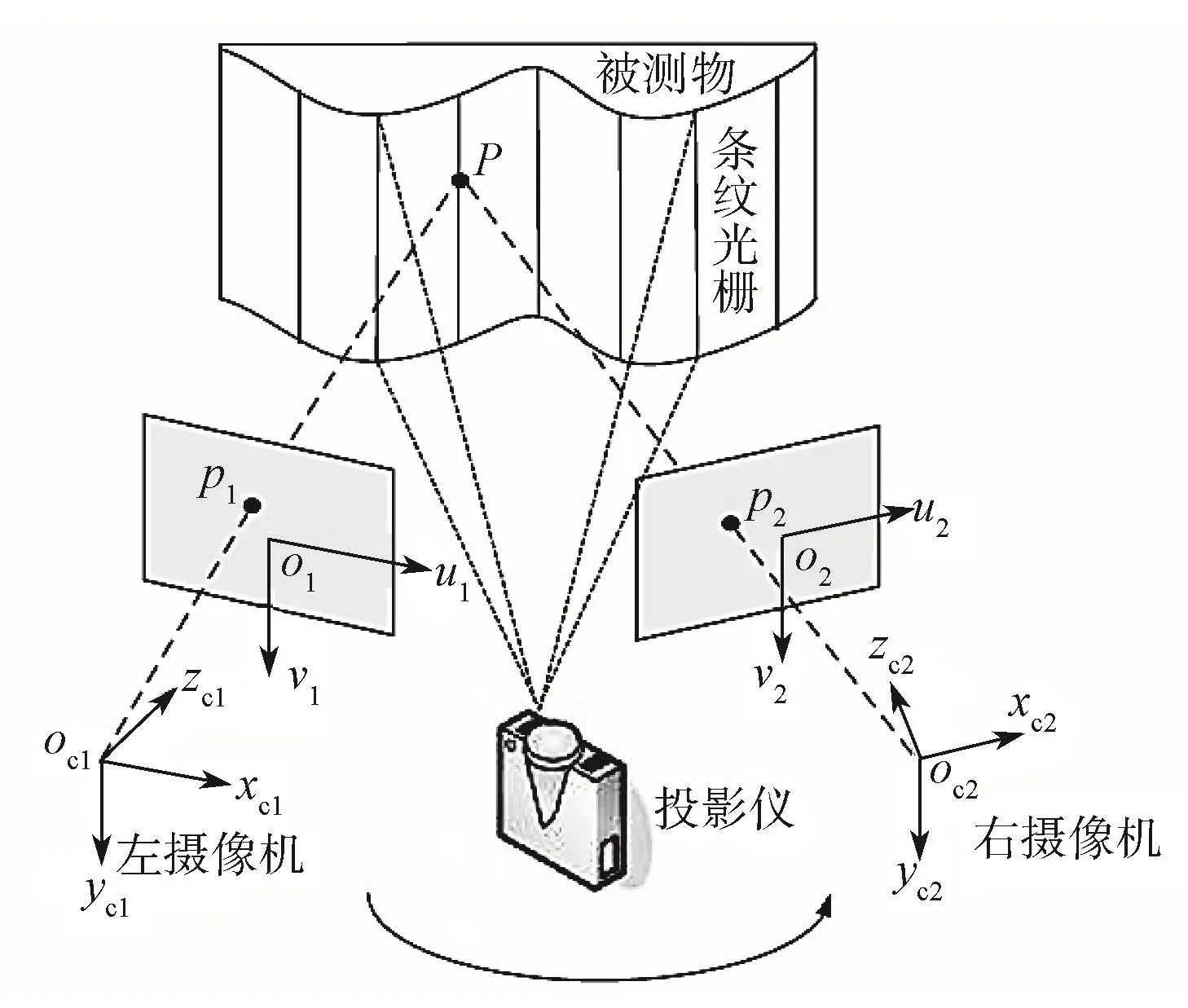
图1 双目结构光原理图Fig.1 Principle diagram of binocular structured light

为了确定左右相机像素点的映射关系，需要对拍摄的条纹图像进行相位解码，其具体包含了通过像素亮度值求解相对相位的过程与在相对相位基础上进行相位展开的绝对相位求解过程。

1.1 编码结构光相对相位计算

通过计算机能够获得理想的正弦条纹光栅，如图2所示。

图2 正弦条纹光栅Fig.2 Sinusoidal fringe grating

光强函数[5-7]可由式（1）表示：

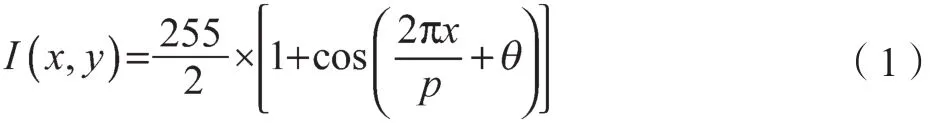
式中：(x, y)——图像像素索引；p——单根条纹在一个周期内的像素值，即条纹节距；θ——相移量，光栅的变化方向是沿着x轴方向变化。

常见的相移算法有很多种，包括2+1相移法、双3步相移法、梯形相移法、标准N步相移法、三角形相移法以及Hariharan 5步相移法等[8]，其中标准N步相移法能够最大程度地压制系统的随机噪声且不会影响(N-1)次以下的谐波[9]。由于标准4步法具备优良的误差容忍能力和超高的测量精度等优势，比较常用[8]，因此本次研究中也运用这一方式。

标准4步法运用的4幅图案分别是0, π/2, π/3和π/4的相移量，所以其理想的光强函数可列为

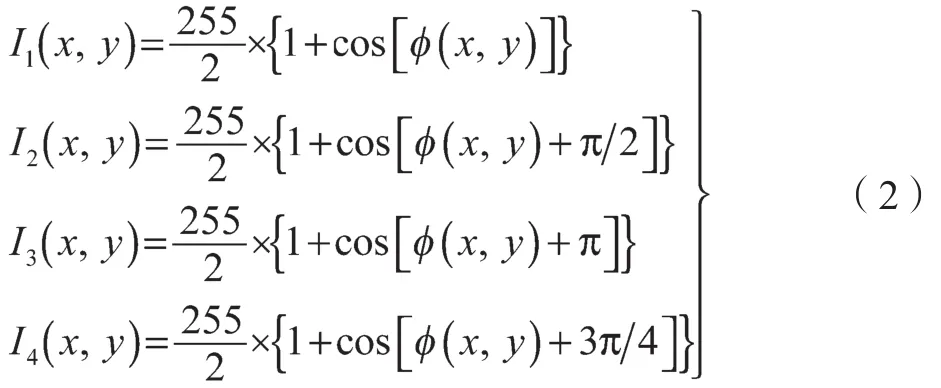
根据式（2）可以计算出光栅图像的相对相位（包裹相位）为

求得的相位值以反正切函数的形式表示，其值被限制在（-π, π）中，其在全场范围内不是连续变化的，且和真实的相位值相差2kπ（k为正数）。由于图像全场范围内存在多个非连续的相对相位周期，故同一相位值在图像上对应多个像素点，这导致了相对相位在图像中的不连续性和二义性，需要展开相对相位，以获取全场范围内唯一的绝对相位。

1.2 相位展开法

根据在相对相位变化方向上加减2π值即为相位展开的基本原理，该原理可以通过式（4）表达：

相位展开算法由时间相位展开算法和空间相位展开算法这两大部分组成。时间相位展开算法主要是通过另外加入一个或者多个其他相关信息，进而能够从根本上弥补相位不连续性的缺陷；而空间相位展开算法则不可以应对位处独立区域的物体及表面变化比较明显的物体。从效果上来看，时间相位展开算法里多频外差展开算法要更有效些[10-12]，多频外差展开法的原理是，将两种及两种以上不同频率的相位函数叠加以得到一种频率更低的相位函数，如图3所示。

图3 多频外差展开原理图Fig.3 Schematic diagram of multi-frequency heterodyne expansion

把不同频率的光栅信号通过叠加处理得到其他频率光栅信号的这一过程称作频率外差。若将光栅1的节距设为λ1，光栅2的节距设为λ2，则式（5）可以表示外差展开后得出的新光栅的节距：

同时，式（6）表示新光栅的相对相位：

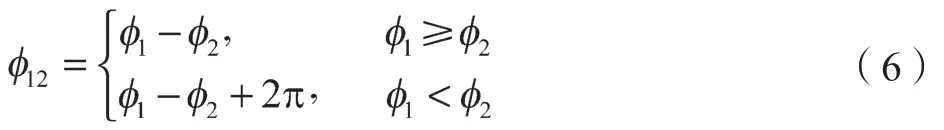
通过挑选合理的光栅节距λ1和λ2，对其进行外差得到的新光栅节距λ12大于原始的光栅节距λ1和λ2，也就表明新光栅在图像内的相对相位是展开的。

下面使用三频外差法对相位展开原理进行解释。先设置3个不同节距(λ1, λ2和λ3)的光栅，其中节距为λ12的新光栅12是光栅1和光栅2外差所得出的，而节距为λ23的新光栅23是光栅2和光栅3外差所得出的，而节距为λ123的新光栅123是新光栅12和新光栅23外差所得出的。

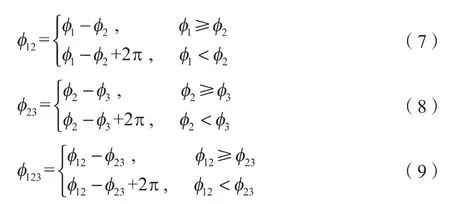
将图像中某一个点的条纹级数设定为n，并以Δn表示小数部分，以N表示整数部分，能够得出的关系式如下：

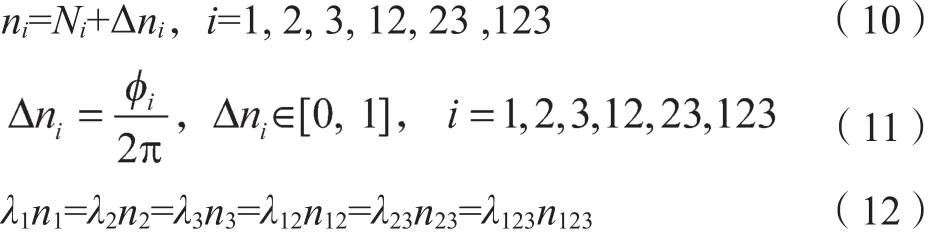
展开后得出的绝对相位值如下：

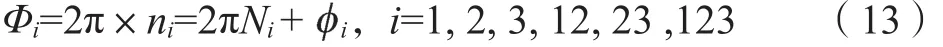
因需要确保第二次外差后得到的新光栅节距将覆盖全场，所以N123=0；可以通过式(10)、式(11)和式(12)得到N12和N23的计算公式，具体如下：

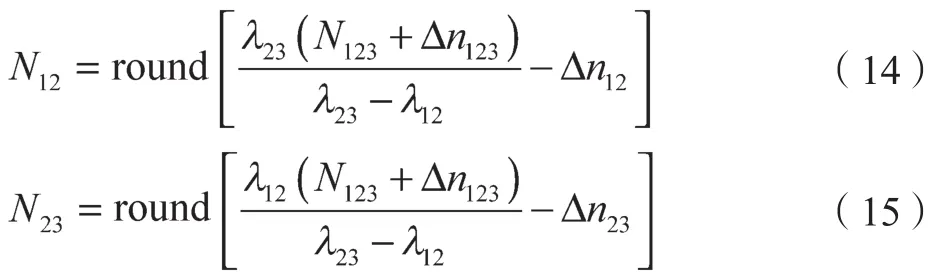
这里，round[]代表将得到的结果取整。

还可以根据式(10)、式(11)和式(12)推导得到N1,N2和 N3：能够得到Φ1, Φ2和Φ3的最终结果：

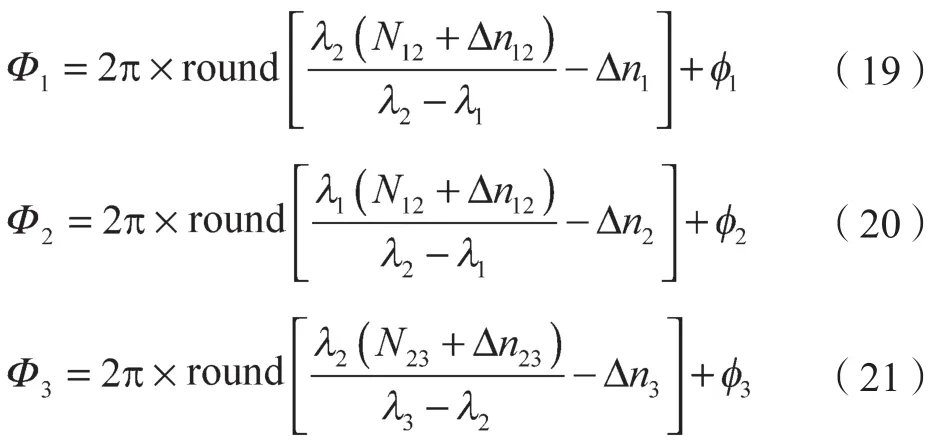
综上所述，全部的计算过程是，通过第二次外差后需全场覆盖这一要求，可以算出N123=0，进一步得出N12和N23的结果；然后结合得到的N12和N23的结果推算出N1, N2和N3的值，最终能够将Φ1, Φ2和Φ3的结果计算出来。因此按照顺序算出N123, N12, N23, N1, N2和N3的值是整个求解过程的最重要环节。

2 立体匹配与三维计算

在得到像素点的绝对相位值后，需要对左右图像进行遍历，以确定左右像素点之间的映射关系，该过程即被称为立体匹配。而三维计算则是在确定了映射关系后，结合相机标定参数，利用三角测量法求解得到像素点对应的空间点坐标的过程。

2.1 立体匹配

在进行三维数据获取的过程中，立体匹配目的是获得两幅图像中对应着同一个空间点的匹配像素点。通过视差之间的关系，进行空间位置的数据信息获取，按照相位匹配的方法对图像中的所有像素进行匹配。通过把图像中各个像素点所具有的极线斜率作为匹配依据，同时结合相位相等的判断条件，完成整个图像范围内像素点的匹配过程。这种方式在抗噪水平、匹配速度和精度方面都存在不错的表现。

在实际操作过程中，首先构建约束，通过约束来降低匹配过程中的计算量。约束形式多样，主要有唯一性约束、连续性约束和外极线约束等。在立体匹配的过程中，外极线约束的运用最为常见，其基本原理如图4所示。

图4 外极几何示意Fig.4 Outer pole geometry sketch

图4 是对外极线约束对应关系的基本展示。从图中能够得出，左极线上的点都能够在右图像的右极线上找到相对应的点；同理，右极线上的任一点pr在左图像上的匹配点也一定能够在左极线LPl上找到。所以运用该约束进行实际匹配时，通过图像上的二维搜索到一维搜索的转变，就能够在很大程度上简化计算流程，降低计算量，实现匹配效率的提升。

2.2 基于“极线斜率-相位”查找库的快速匹配

为尽可能提升立体匹配的速度，本文通过构建“极线斜率-相位”的方式进行查找容器的形成，相较于之前在极线校正基础上进行的相位匹配，这种方式可以通过大幅降低匹配点的查找范围而提升匹配的精度和速度。其基本流程如图5所示。

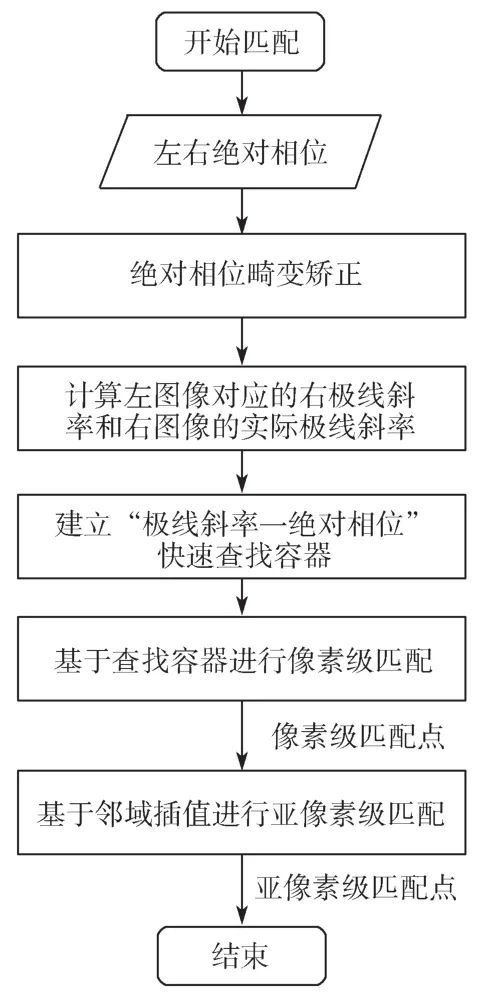
图5 快速匹配算法流程Fig. 5 Flow chart of the quickly matching algorithm

该匹配方式的基础就是左右相机的位置保持稳定，将其旋转矩阵和平移矩阵设定为R和T，其中ri(i=1,2, …, 8, 9)与tk(k =x, y, z)分别为矩阵R和T内的元素，如式（22）所示：

针对空间中的一点p，假定其在左图像中的图像为pl，将其与El相连可以得到左极线LPl，其斜率的计算方式是左图像中取两点坐标进行计算，并记为kll；则该极线向右图像平面进行转化后的斜率klr可以按照式(23)求得[13]：

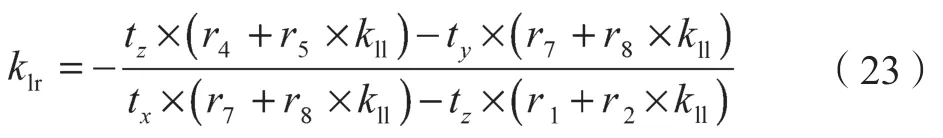
同理可以求出右图像中的点pr在极线上的斜率向左图像进行转化后的斜率krl为

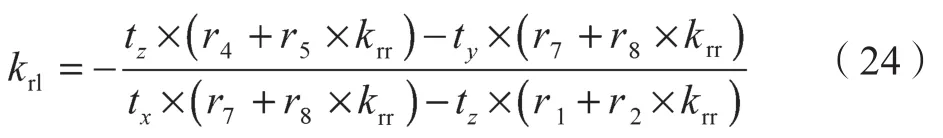
该算法的基本步骤如下：

（1）运用标定数据执行矫正过程，然后以双线性插值法获得经过矫正之后的相位图；

（2）进行右极线的斜率和实际斜率值的计算，并将所得的结果替换为极线角度值存储起来；

（3）创建匹配数据库，在每个子数据库中存储的是某个范围中的图像像素点的集合，并能够实现全部像素点的涵盖；

（4）匹配的初始时期，应该首先针对像素点的初始匹配点进行具体的计算；

（5）经过图像比对对最终匹配点进行确认，所得即为亚像素级匹配。

2.3 立体匹配背景分割

为了尽可能地提升匹配效率，在实施光栅投影时，通过采集白光图并运用灰度期望法[13]将背景进行分割，加上背景掩码（图6）后，再进行背景计算，得出相应结果之后再进行点云的拼接计算。

图6 匹配背景分割示意图Fig.6 Schematic diagram of matching background segmentation

2.4 三角测量法

获得图像的匹配点集后，利用三角测量法结合相机标定参数可以恢复被测物体的三维信息，从而进行测量。

“极线斜率-相位”的匹配方式是建立在非平视双目几何结构上而实施的。设定左相机焦距为fl、右相机焦距为fr，所得匹配点对为(Xl,Yl)和(Xr,Yr)，左相机到右相机的变换矩阵M可表示为

那么三维点的计算公式如下[14]：

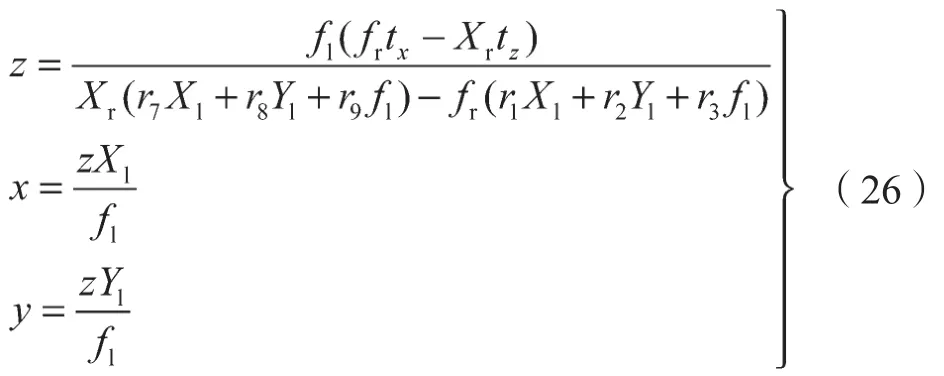
3 高铁白车身测量实验

以高铁白车身侧墙为测量对象进行实验，在实际测量过程中要求：（1）测量范围广泛，保证覆盖全部车身；（2）精度高，要求误差不得超过0.5 mm/m；（3）速度快，超过0.15 m/s。基于此，开展了下述实验工作。

3.1 双目结构光硬件平台

本次设计中系统部分包括了TI制造的DLPLightCrafter4500TM型投影仪，其分辨率在1280×800左右；相机则使用的是Basler制造的acA2040-35gm型面阵相机，其镜头使用的是FUJINON公司制造的HF12XA-5M型镜头，分辨率为500万，焦距为12 mm，其光圈值F为1.6-16。

系统的硬件布局如图7所示，其中相机被置于投影仪的两侧，调节左右相机角度（在不同角度下进行测量，即视角1与视角2），使之具有较大的重叠视野区域；为使系统获得更稳定的测量结果且尽可能地利用投影仪的投影幅面，三者应保持在同一水平高度。

图7 系统硬件布局Fig. 7 Layout of the system hardwares

3.2 相机标定

本研究中标定方式采用传统的张正友标定法[14]，即在OpenCV的基础上进行相机标定。对玻璃材质精度要求比较高的标定板进行了6次实验，实验误差（标定板两特征点之间测量距离和实际距离之间偏差的 RMS 值）结果如表1所示。由表1可知，各组实验结果皆满足高铁白车身测量实验所要求的0.5 mm/m的精度，特别是第六次实验中，系统的RMS误差达到了0.093 mm/m，这验证了该标定方法的可行性。

表1 6次标定实验误差结果Tab.1 Error results of six calibration experiments(mm/m)

3.3 测量实验

选取高铁白车身上宽约为1 m、高约为1.2 m、中间位置有弧形、表面有待打磨腻子的侧墙板（图8）展开测量工作。由于实际的高铁白车身具有大幅度的表面，故需要在不同视角下对其进行多次测量，并通过点云拼接技术以获得最终完整的高铁表面点云数据。运用多频外差展开法进行后续操作，图9是对节距（条纹宽度）分别为21、23、25像素的条纹图案进行投影时，通过左相机在两不同视角下拍摄得到的条纹图像。

图8 测量对象及装置布置图Fig. 8 Arrangement of measurement object and device

图9 在不同视角和不同节距下的条纹图Fig. 9 Fringe patterns at different angles and different pitches

在利用多频外差相位法完成展开计算之后，把图9（a）和图9（b）的条纹光栅作为基准继续进行匹配，图10是视角1与视角2中得出的左右相位图。

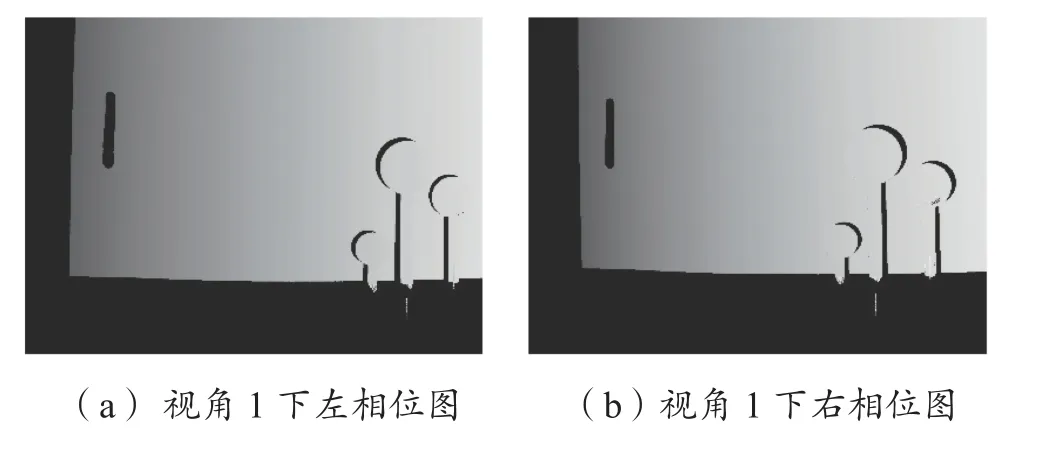
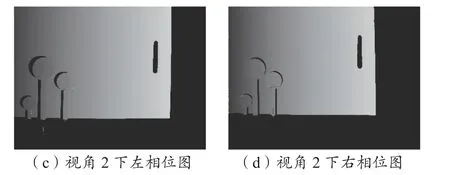
图10 绝对相位图Fig 10 Absolute phase diagram

运用相位匹配和三角测量的方式能够准确获得视角1与视角2的点云，对直径为50 mm的标准球进行拟合，视角1所得的直径为50.02 mm（图11），视角2的为50.24 mm（图12）。之后开始针对上述视角中的点云执行拼接操作，拼接前后的点云比对图以及拼接所得的重叠区域分别如图13和图14所示。

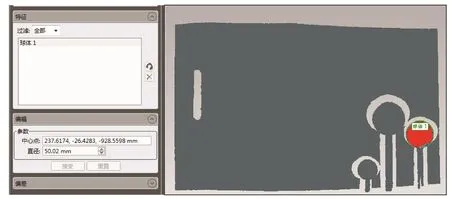
图11 视角1下50 mm标准球拟合结果Fig. 11 Fitting results of 50 mm standard ball in perspective 1

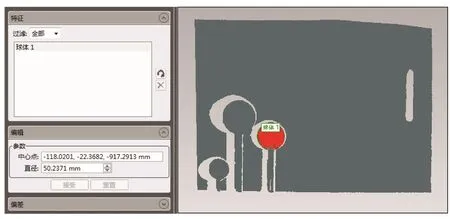
图12 视角2下50 mm标准球拟合结果Fig. 12 Fitting results of 50 mm standard ball in perspective 2

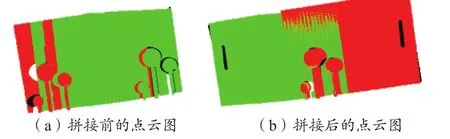
图13 点云图对比Fig. 13 Comparison of point cloud images

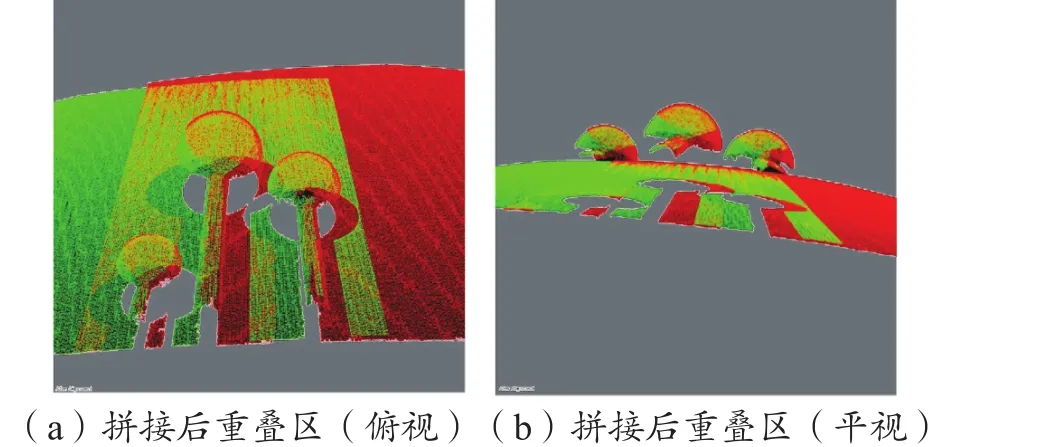
图14 拼接后重叠区放大图Fig. 14 Enlarged images of overlapping region after splicing

将拼接之后的直径为50 mm的标准球与点云进行球面拟合操作，所得出的结果如图15所示。剔除含有拼接部分的数据，经过重构之后所得结果如图16所示。可见，经过重建之后所获得的车身样本数据信息更加精确。

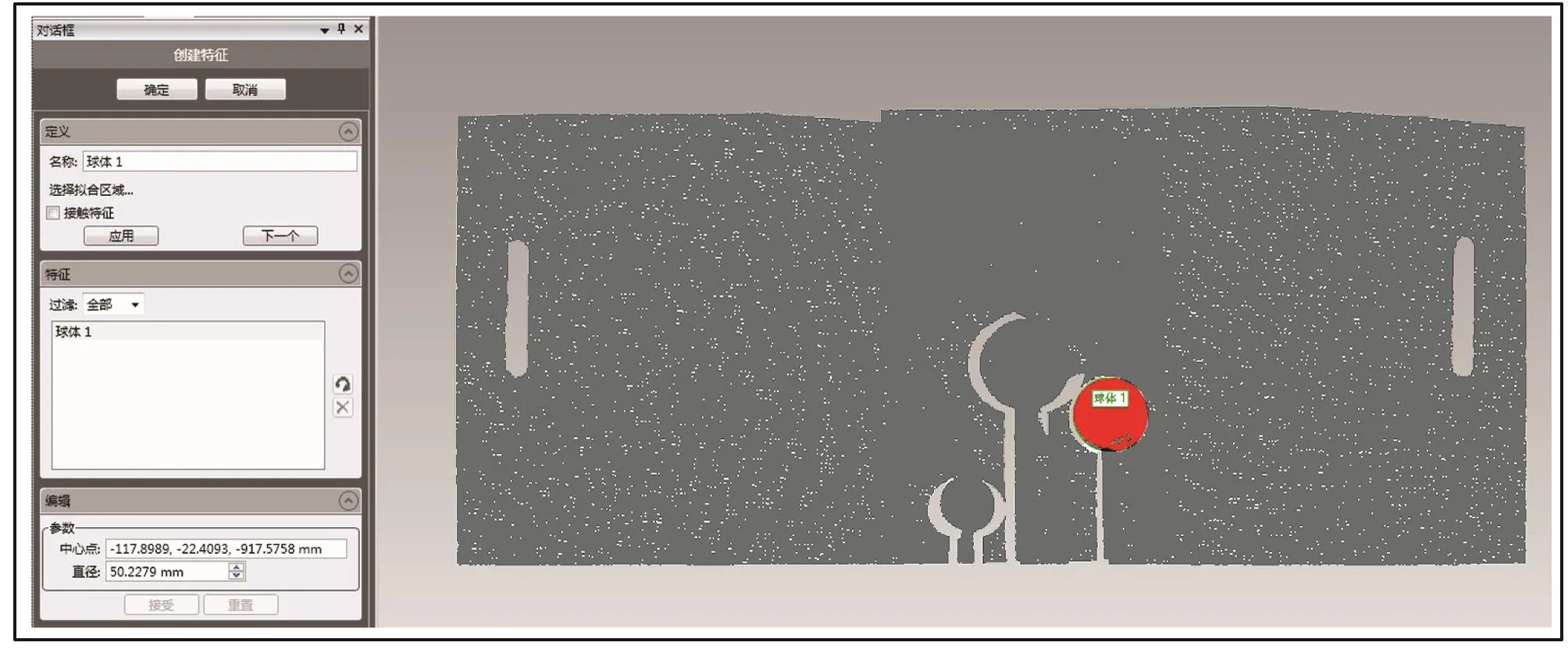
图15 拼接后标准球拟合结果Fig. 15 Fitting results of standard balls after splicing

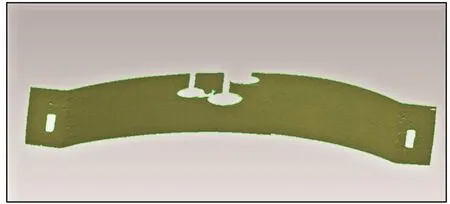
图16 重建结果Fig. 16 Reconstruction results

3.4 实验结果分析

通过上述实验及图15中软件计算可得如下结论：50 mm的标准球，其拟合直径为50.227 9 mm，与进行拼接之前的拟合直径对比，误差为0.07 mm/m。因此，所设计的系统其测量精度不超过0.5 mm/m，满足精度要求。

从测量速度来看，所设计的系统测量时间包括了投射、采集以及计算这3个环节的时间，前两个环节的操作所消耗的时间共为1 s左右，而数据计算消耗的时间在1.5 s左右，则累计消耗时间为2.5 s，从而得出测量的速度保持在0.4 m/s，符合高铁白车身对于测量速度的要求（高于0.15 m/s）。所以，这一双目结构光测量方法在很大程度上满足了高铁白车身对于测量速度和测量精度的要求。

4 结语

本文研究了一种基于双目结构光的三维测量技术，用其对高铁白车身表面的质量实施有效的评估和测量，并运用多频外差相位展开法实施具体的相位展开；首次提出了以构建“极线斜率—相位”的方式形成查找容器，提升了实际匹配过程中的计算效率。利用这一匹配方式可以快速实现粗定位，并且最终得到像素级的匹配点位；利用所得到的点位进行更加精准的查询，得到亚像素级匹配；此外，在实际的匹配过程中可以将错误的匹配点进行提前删除，有效提升了匹配效率和精度。高铁白车身测量实验表明，双目结构光的测量精度达到0.07 mm/m，满足测量的精度需求（＜0.5 mm/m）；其测量速度为0.4 m/s，满足高铁白车身测量速度的要求（＞0.15 m/s）。然而整个测量方法在测量精度与速度方面还可以有进一步的提升空间，如通过多个双目结构光设备形成更大的测量视场，可进一步提高测量速度。