基于光学动作捕捉的室内移动机器人轨迹跟踪
2020-07-23吴文辉
吴文辉,唐 炜,王 勇,陈 清
(1.江苏科技大学机械工程学院,江苏 镇江 212003;2.徐州市质量技术监督综合检验检测中心,江苏 徐州 221000)
0 引言
定位技术是移动机器人轨迹跟踪控制中最基本的环节,在室内环境下,机器人的定位精度一般要求在厘米级。常见的室内定位技术包括基于编码器和惯性传感器的相对定位、Wi-Fi定位、无线射频标签(RFID)定位、超宽带(UWB)定位和ZigBee定位等。文献[1]基于航迹推算和无线射频识别技术相结合的定位方式,使移动机器人的定位误差控制在20 cm内;文献[2]基于UWB技术用ADS-TWR测距,并采用卡尔曼滤波定位,使定位误差控制在13 cm内;文献[3]基于ZigBee技术对移动机器人的三边定位进行研究,使定位误差在5~7 cm之间,但当机器人离固定节点30 cm内无法定位。由于移动机器人的定位精度无法得到保证,导致对移动机器人轨迹跟踪的研究大多还停留在仿真阶段,没有真正地投入应用。基于标记点的光学动作捕捉系统定位精度可达亚毫米级[4],在要求高精度定位的室内场合下,应用广泛,如OptiTrack通过对四轴飞行器进行实时跟踪定位,实现了飞行器集群的协作。本文将采用基于标记点的光学动作捕捉系统对移动机器人进行定位。
针对移动机器人的轨迹跟踪控制,常用的方法包括反演法[5]、滑模控制[6]、神经网络法[7]和模糊控制[8]等。其中滑模控制是一种非线性控制方法,由于滑模控制律易产生抖动,使得系统不够稳定;神经网络法虽然不依赖模型,并能够消除系统的不确定性和未知扰动,但在线学习时间长,控制算法较为复杂;模糊控制无需建立精确的数学模型,但是模糊规则的选择缺乏系统性,且无法实现在线调整。反演法因其在保证系统稳定性的同时又具备控制器设计的灵活性,所以成为实际工程应用中最普遍的方式[9],本文将采用反演法对移动机器人的轨迹跟踪器进行设计。
1 光学动作捕捉原理
基于标记点的光学动作捕捉系统需要在被测场地上布置多台红外相机,记录被测对象上光学标记球的反射光线,并将光学标记球信息存储为灰度图,通过霍夫变换确定标记球在二维图像中的几何中心位置,最后对多个相机中二维图像中标记球的位置信息进行处理,计算出标记球的空间坐标。具体而言,当同一个标记球被2台以上的摄影机同时拍摄到,则可根据相机参数和计算机视觉原理重建出标记球在三维空间中的坐标信息,具体的重建过程如图1所示。

图1 3D坐标点重建示意
令P1和P2为空间点P在相机C1和相机C2图像中的点,同时2个相机都已经标定完毕,将相机C1和相机C2对应的投影矩阵记为M1和M2,于是有:
(1)
(2)

(3)
(4)
(5)
(6)
式(3)~式(6)中,只有3个未知量,故该线性方程组必然存在解,且解是唯一的。然而,由于数字图像中数据噪声的存在,4个等式中任何3个联立得到的答案可能都不一样,使用最小二乘法来求解可使误差最小化,当相机C1中的点P1和相机C2中的点P2互相匹配,便能计算出点P的空间坐标。如果被测物体为一刚体,在被测物体上固定有至少3个不共线的光学标记球,且光学标记球不会随着被测物体的移动而发生位置的改变,则可对这些光学标记球建立模型,基于标记点的光学动作捕捉系统通过对模型的识别以及跟踪[10],便能实时获取到刚体的位姿信息。
2 轨迹跟踪器设计
2.1 运动模型建立
本文研究对象为一款基于麦克纳姆轮的全向移动机器人,能够实现全方向的移动,具有3个自由度,即沿x轴和y轴的平动以及绕z轴的转动,其中轮毂轴线与辊子轴线的夹角为45°,整体的布局方式如图2所示,并在其几何中心建立局部参考坐标系xoy。
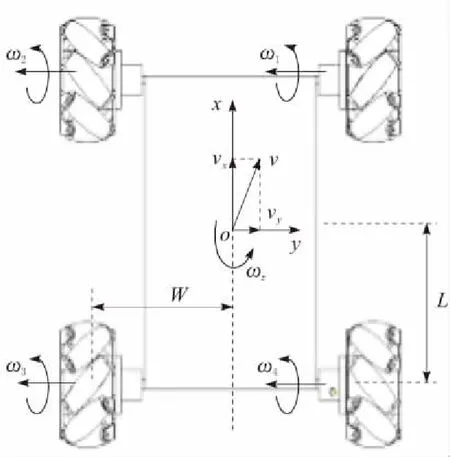
图2 全向移动机器人示意
假设麦克纳姆轮与地面接触充分且无打滑现象,且移动机器人的平台重心与其几何中心重合。通过对移动机器人车体速度与车轮转速之间的关系进行分析[11],可得到全向移动机器人的正向运动学方程为
(7)
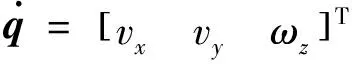
因为雅克比矩阵J的秩rank(J)=3,故全向移动机器人不存在奇异位形,根据广义逆运算可得到移动机器人的逆向运动学方程为
(8)
J+为雅克比矩阵J的广义逆矩阵。
2.2 位姿误差模型建立

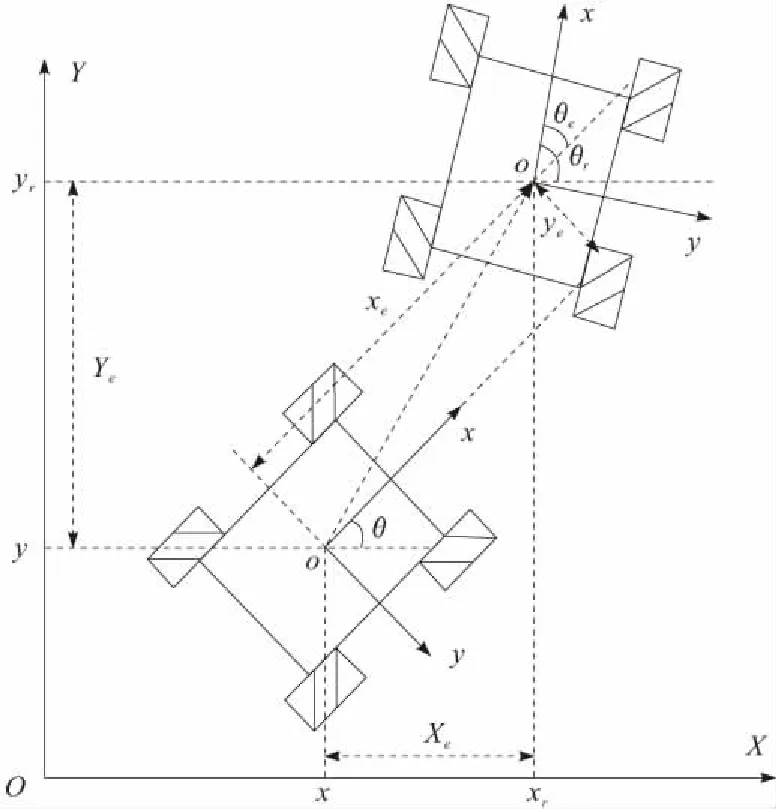
图3 位姿描述示意
根据坐标变化公式可以得到机器人全局位姿误差与局部位姿误差之间的关系为
(9)
进一步化简可得
(10)
设定移动机器人在局部坐标系中的速度vx为全局坐标系中的速度v,即vx=v,vy=0。为了便于描述,将沿X轴方向的速度vX与沿Y轴方向的速度vY合成为v,其中vX=vcosθ,vY=vsinθ。
对式(10)求微分,可得
(11)
2.3 轨迹跟踪系统设计
移动机器人的轨迹跟踪控制系统结构如图4所示,该控制系统的输入变量为参考位姿Pr、实际位姿P和参考速度ur,其中参考速度由参考线速度vr和参考角速度ωr构成。控制器根据参考位姿Pr与实际位姿P进行比较,得到全局位姿误差E(t),通过坐标转换得到局部位姿误差e(t),其次将系统位姿误差e(t)和参考速度ur作为轨迹跟踪器的输入得到机器人平台的期望速度u,根据运动学模型得到每个车轮的期望转速,通过速度控制器便能实现整个平台的运动,最后光学动作捕捉系统对移动机器人的位姿P进行实时采集并反馈给移动机器人,根据此流程反复对轨迹跟踪控制器进行调节,从而使移动机器人的位姿误差趋于零。
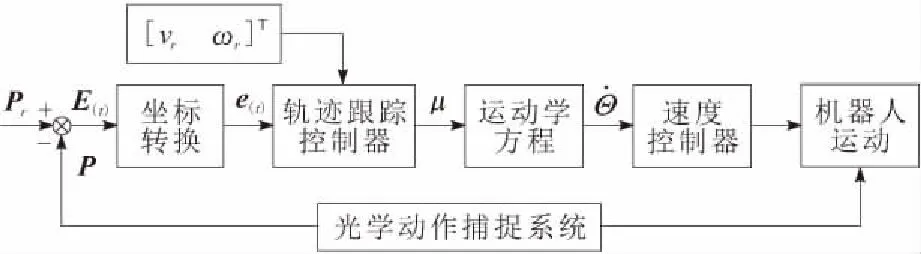
图4 轨迹跟踪系统结构
为了实现轨迹跟踪的目的,将xe作为虚拟控制输入:
(12)
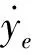
(13)
对式(13)求微分可得
(14)
将xe代入式(14)可得
(15)
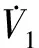
(16)
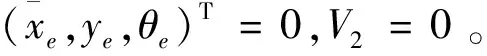
对式(16)求微分可得
(17)
(18)
将式(18)代入式(17),可得
k1sin(arctanω)(-ωxe+vrsinθe)-v+vrcosθe]-
(19)
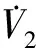
(20)
k1、k2和k3为任意的正常数,k1对xe进行调节,k2、k3分别对ye和θe进行调节。
3 测试平台搭建
本文采用的光学动作捕捉系统包括6台光学动作捕捉相机,具体型号为OptiTrack Prime13、运行Motive软件的上位机PC和支持POE功能的千兆交换机,其中上位机PC与光学动作捕捉相机通过六类网线连接至千兆交换机,并将多个光学标记球通过支架固定在移动机器人上,整个测试环境如图5所示。在上位机软件Motive中,将固定在机器人底盘的光学标记球选中使之成为RigidBody,将其命名为robot,便能实时获取到所选光学标记球几何中心的位姿信息,由于移动机器人的底盘为刚体,且光学标记球与移动机器人底盘为刚性连接,所以获取的数据信息可当作移动机器人整体的位姿信息,同时在Motive中将上位机配置为VRPN[13](virtual-reality peripheral network)服务端。
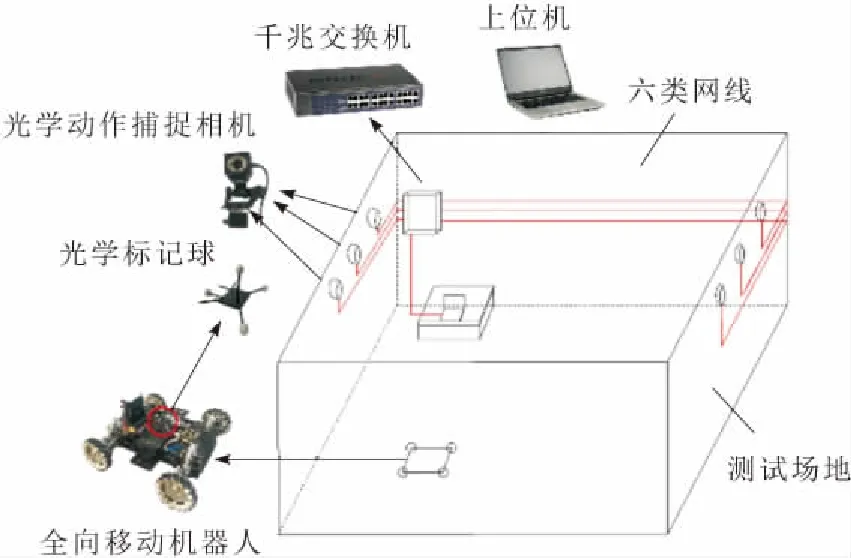
图5 测试环境示意
全向移动机器人的每个车轮都由单独的电机独立控制,其硬件模块主要由树莓派、基于STM32的主控板、4个电机驱动器和4个直流电机组成,硬件模块连接情况如图6所示。安装在机器人上的树莓派是室内移动机器人的控制核心,是一款运行Linux操作系统的开源卡片电脑,将其与上位机PC连接在同一个局域网下,基于ROS[14](机器人操作系统)安装相关的功能包将其配置为VRPN客户端,通过VRPN协议便能实现上位机PC与树莓派的数据交互。

图6 硬件模块连接示意
当树莓派与上位机成功建立连接后,ROS中会产生额外的Topic-/vrpn_client_node/robot/pose,该话题的主要内容为移动机器人的位置信息与姿态信息。在ROS中新建节点设计轨迹跟踪器,通过订阅该话题获取机器人当前的位姿信息作为轨迹跟踪器的输入,输出为移动机器人的期望速度,并使用高速串口发送给主控板。主控板接收到数据后,通过运动学方程将其转化为4个电机的期望转速,并由CAN总线发送给电机控制器,电机控制器运行增量式PID控制算法对直流电机进行实时调速,最后电机驱动麦克纳姆轮从而实现整个移动机器人的运动。
4 仿真与实验
为了验证所研究控制算法的可行性,通过在MATLAB环境下对移动机器人的直线轨迹和圆周轨迹的跟踪过程进行仿真,同时将仿真的参数设置到试验样机中,在光学动作捕捉系统的测试环境内,利用其对移动机器人进行实时定位,并令移动机器人按照给定的轨迹进行移动,同时记录机器人在实际移动过程中的位姿信息。
4.1 直线跟踪实验
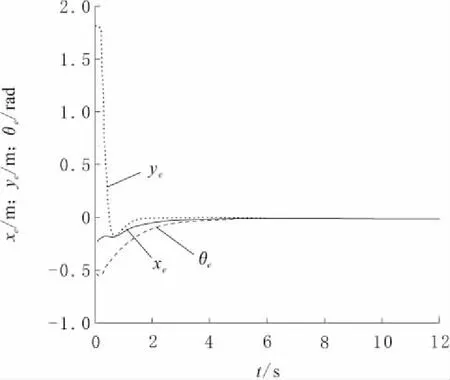
图7 位姿误差时间响应曲线
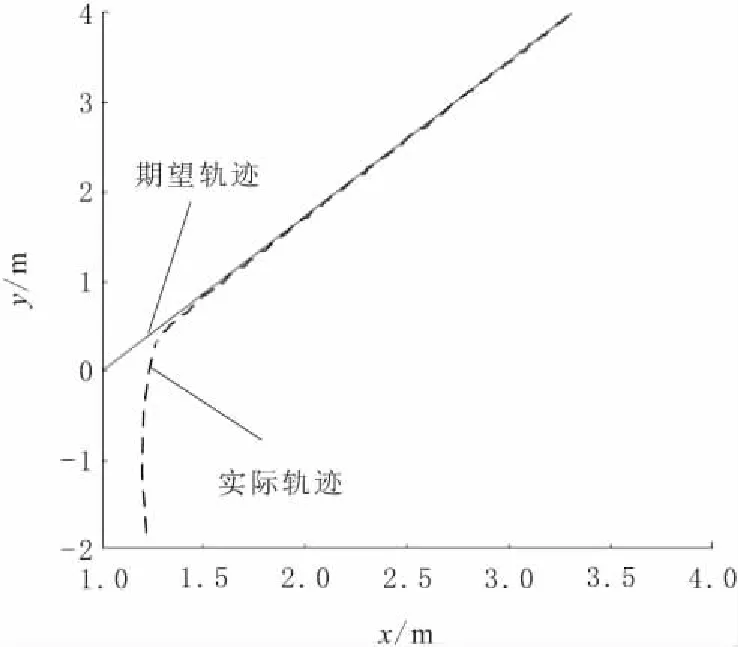
图8 实际直线轨迹跟踪效果
4.2 圆周跟踪实验
设定移动机器人的参考运动轨迹为Xr=cos(0.2t),Yr=sin(0.2t),θr=π/2+0.2t,即给定轨迹为半径1 m圆周;令参考输入为vr=0.25 m/s,ωr=0.2 rad/s;在全局坐标系下初始参考位姿为xr(0)=1 m,yr(0)=0,θr(0)=π/2 rad;同时移动机器人在全局坐标系下的初始位姿为x(0)=1.25 m,y(0)=-0.2 m,θ(0)=2π/3 rad;取k1=5,k2=5.2,k3=2.2。仿真环境下的位姿误差时间响应曲线如图9所示,真实环境下的圆周轨迹跟踪效果如图10所示。
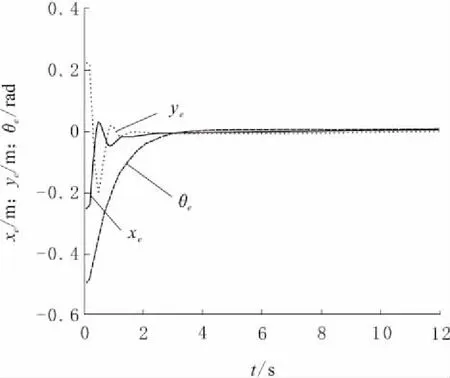
图9 位姿误差时间响应曲线

图10 实际圆周轨迹跟踪效果
由图7和图9可看出,在仿真环境下,移动机器人最终收敛于参考轨迹,其中直线轨迹为3.8 s左右,圆周轨迹的收敛时间为3.2 s左右,同时发现不同的参考轨迹、参考速度以及机器人的初始位姿都会对参数k1、k2、k3产生影响;由图8和图10可以看出,通过在仿真中选取合适的参数,实际运行过程中,虽然全向移动机器人存在车轮打滑的情况,但在本文设计的跟踪控制系统作用下,其实际轨迹一直趋于参考轨迹,且偏差较小。仿真结果表明,使用基于标记点的光学动作捕捉系统采集机器人的实时位姿,并将其位姿信息加入控制回路中,可以令全向移动机器人拥有良好的轨迹跟踪效果。
5 结束语
自主搭建了1台基于麦克纳姆轮的全向移动机器人,利用基于标记点的光学动作捕捉系统对其进行实时追踪定位,并将光学动作捕捉系统获取的位姿信息作为移动机器人控制系统的输入。利用反演法构造出一种全局渐进稳定的轨迹跟踪控制器,通过MATLAB仿真证实了该控制方法的有效性,并在自主搭建的试验样机进行验证。结果表明:通过对轨迹跟踪器选取合适的参数,可使移动机器人获取良好的轨迹跟踪性能,同时利用基于标记点的光学动作捕捉系统精确定位的特性,能够为移动机器人的室内导航以及运动检测提供一种新的解决办法。
