基于响应面法的超压艇结构优化设计

侯守武，王平安，成 琴

(1.中国电子科技集团公司第三十八研究所，安徽 合肥 230088;2.国家级工业设计中心(中电38所)，安徽 合肥 230088)

0 引言

平流层气球驻空飞行在20 km以上的高空，昼夜温差较大，使高空气球气压变化超过1 000 Pa[1]，传统的零压球通过排气和释放压舱物保持气球升空高度，缩短了飞行时间，超压气球采用高强度的薄膜材料和封闭式的结构，可以承受温度升高引起的超压，适用于高空长航时环境。

国内外学者对高空气球的材料和结构设计开展了相关研究。Cutts等[2]使用特殊材料膜材料制作了正球形超压气球，正球形结构的承压能力取决于材料的强度性能；Barg等[3]建立了南瓜形超压球结构的数学模型，分析了加强筋结构对球体强度的影响；韦利军等[4]利用Isight软件对南瓜型高压球的加筋结构布局和尺寸进行了优化，并利用试验进行了验证；程士军等[5]分析了超压气球结构的加强筋数量对结构受力和变形的影响，加强筋数量增大后，蒙皮经、纬向应力值下降幅度达到64.4%；Saito等[6-7]提出了一种网状加强形超压气球结构，具有良好的承压能力，但囊体外表面需铺设较多绳索，可靠性较低；杨其等[8]采用等强度设计准则设计索网蒙皮结构超压气球，提高了材料的利用效率。目前，学者主要集中在南瓜型和索网型超压球结构研究，椭圆形超压艇结构的加强筋间距、筋直径、筋间瓣幅曲率半径等设计参数对强度的影响，目前尚未见到相关研究。

本文以超压飞艇为研究对象，以加强筋间距、加强筋直径、加强筋间瓣幅曲率半径3个参数为设计变量，利用Box-Behnken试验设计(BBD)，基于响应面法建立囊体结构应力及加强筋质量与3个参数的二次多项式函数，以囊体结构应力为优化目标，加强筋质量为约束条件，构建优化确定合理的加强筋设计参数，为超压艇的结构设计提供支撑。

1 超压艇结构的应力分布特性

本文以压差1 500 Pa状态的 10万 m3超压艇为分析对象，基于有限元法分析超压艇体结构的应力分布。有限元模型中，囊体和筋分别采用膜单元和truss单元建模。图1给出了未加筋和加筋2种结构的应力分布。

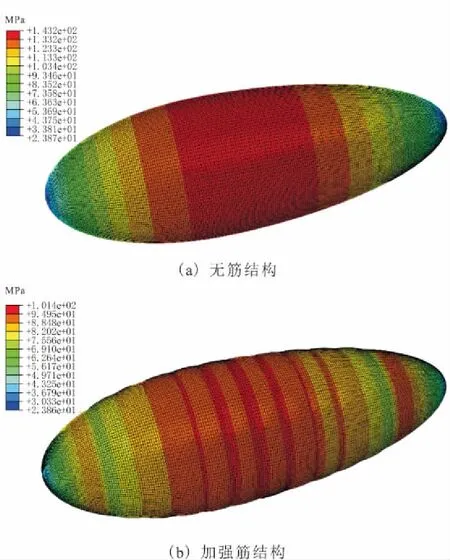
图1 超压艇结构应力分布

由图1可知，未加筋结构最大应力为143.2 MPa，位于艇体中间区域，布置加强筋后，加筋区间内的应力得到了显著降低，加强筋外侧靠近艇体两端的区域应力无变化。因此，艇体应力较大的区域可以通过布置加强筋来降低。加强筋间艇体应力分布主要表现为瓣幅中间区域和加强筋附近区域应力较大，应力大小与筋间距、筋直径、瓣幅曲率密切相关。

2 超压艇结构优化函数的建立

2.1 试验设计与数据提取

超压艇结构优化设计参数包括加强筋间距、筋直径、筋间瓣幅曲率半径，共3个设计参数，分别记为x1、x2、x3。基于Box-Behnken试验设计方法，根据3因子3水平试验设计要求，共有13组试验点，试验点如图2所示。

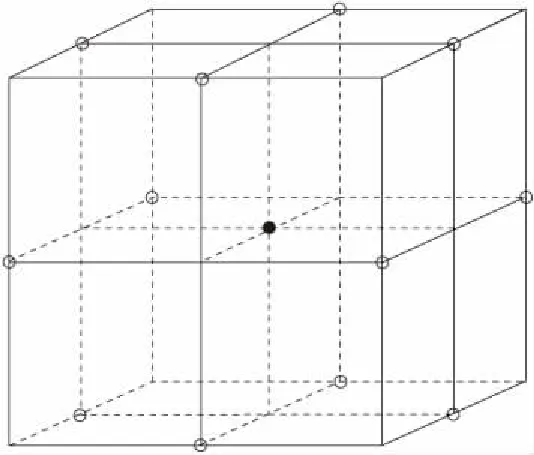
图2 3因子3水平的BBD试验设计

考虑材料和工艺实施的可行性，本文选取的加强筋间距设计范围为3～13 m，筋直径设计范围为16～32 mm，筋间瓣幅曲率半径设计范围为10～30 m，即设计参数x1∈[3,13]，x2∈[16,32]，x3∈[10,30]。表1给出了13组试验结构的计算结果。

表1 不同结构的应力计算结果

2.2 响应面模型建立与误差分析

基于BBD试验设计结构的计算结果，采用二次回归方程拟合得到设计变量与目标函数响应值之间的函数关系，建立响应面模型。

利用响应面法建立的数学模型为

(1)

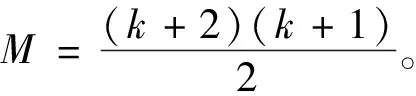
则响应面数学模型为

(2)

在第i个试验点x(i)处，响应面模型y(x(i))与yi的绝对误差为

(3)

则M个试验点处的绝对误差平方和为

(4)

利用最小二乘法，使响应面模型y(x(i))与yi的绝对误差平方和最小，可得基函数系数

a=(ΦTΦ)(-1)(ΦTy)

(5)

y=[y1,y2,…,yN]T，Φ由M个试验点的基函数构成

(6)

基函数系数代入响应面模型，可确定响应面模型数学表达式。

响应面模型的优劣决定了优化结果的好坏，需要对响应面模型的质量进行评价，分析回归方程的精度和误差。工程中常用复相关系数R2评价拟合程度，复相关系数表达式为

(7)

根据BBD试验设计结构的计算结果，综合考虑中间艇瓣幅弧面和筋根部囊体结构的应力，取应力平均值作为研究对象，基函数系数为a=[103.202,5.531,-0.460,-2.952,-0.060,-0.101,0.003,0.036,0.020,0.054]T，复相关系数为0.96，可以满足工程分析。不同的结构设计参数对超压艇体应力影响的曲面如图3所示。

图3 不同参数对应力影响的曲面

2.3 优化数学模型的建立

超压艇加筋结构降低了艇体的应力，但也增加了飞艇的重量，在优化设计时将加强筋质量作为约束条件来限制。

筋的质量与筋的个数和直径有关，而筋的个数与筋间距相关，因此筋的质量的设计参数为筋间距和直径。表2给出了加强筋间距L和筋直径d变化时，超压艇加强筋质量与未加筋结构质量的比值。

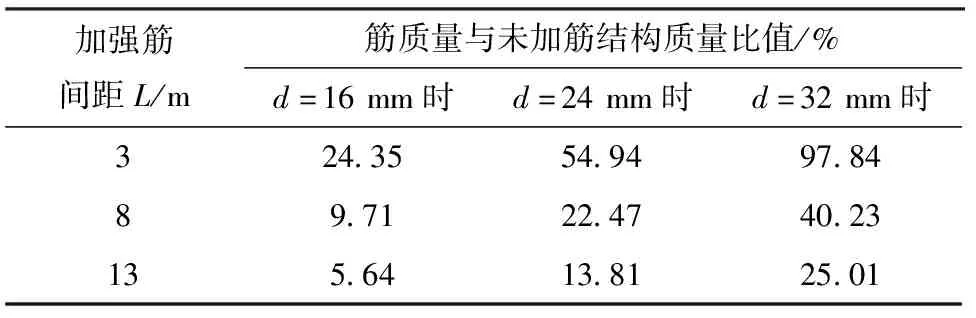
表2 不同设计参数下加强筋质量与未加筋结构质量比值

利用二元二次多项式拟合筋质量与设计参数的响应面模型，其表达式为

m(x)=-146.972-109.353x1+67.181x2-

(8)

筋间距和直径与质量比例的关系如图4所示。随着筋间距的减小和筋直径的增加，附加质量显著增加，筋间距为3 m、筋直径32 mm时，附加质量已接近于未加筋结构的质量。

图4 筋间距和直径与附加质量比例的曲面

以囊体结构加强筋间囊体结构的强度为优化目标，考虑结构重量限制，构建超压艇结构优化响应面数学模型为

(9)

y(x)为目标函数;xjl和xju分别是第j个设计变量的下限值和上限值;m(x)为加强筋质量;m0为未加筋飞艇质量;α为附加质量比例系数的允许值。

3 超压艇结构参数优化

根据之前得到的优化设计数学模型，利用MATLAB软件中的优化函数对超压艇结构设计参数进行优化。为考察加强筋质量对提高强度的影响，表3给出了不同加强筋质量下的最优参数。

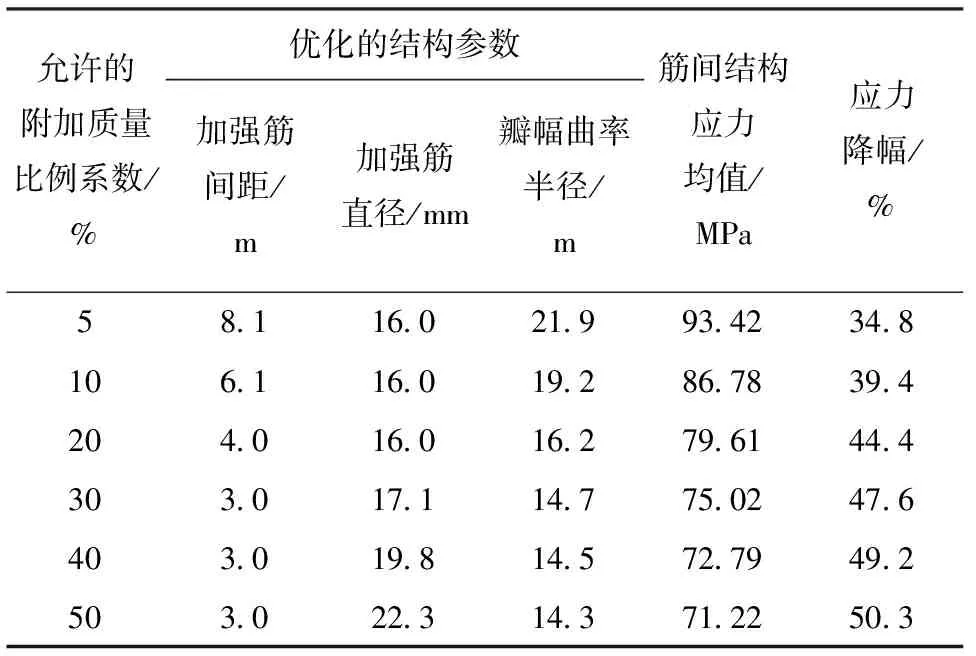
表3 不同允许附加质量下的优化设计结果

由表3可知，加强筋间距、加强筋直径、瓣幅曲率半径3个设计参数表现为强相关性：随着允许加筋质量的增大，加强筋间距逐渐变小而收敛于设计变量下限，而加强筋直径逐渐增大，瓣幅曲率半径逐渐减小；随着允许质量的增加，筋间艇体结构应力逐渐减小，应力降幅逐渐收敛到50%，允许的附加质量比例系数为30%时，即可得到较好的应力控制。

为验证优化设计方法和优化设计参数的有效性，根据优化的加强筋间距、筋直径和瓣幅曲率半径，选取允许的附加质量比例系数30%和50%分别进行有限元验证分析，相应的结构设计参数分别为(3.0 m，17.1 mm，14.7 m)和(3.0 m，22.3 mm，14.3 m)，加强筋间囊体结构应力分布如图5所示。

由图5可知，当允许增加的加强筋质量比例系数为30%时，筋间囊体结构的最大应力为76.10 MPa，响应面模型计算的应力均值为75.02 MPa；质量比例系数为50%时，筋间囊体结构最大应力为71.60 MPa，响应面模型计算的应力均值为71.22 MPa。可见，本文提出的超压艇结构响应面优化模型具有较高的精度，适用于超压艇结构优化设计。

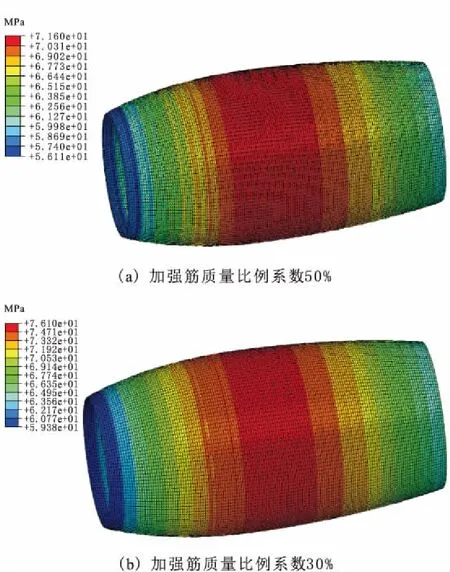
图5 优化的超压艇结构加强筋间囊体结构应力分布

4 结束语

结合BBD法，建立加强超压艇结构的应力响应面模型，研究了加强筋间距L、筋直径d和瓣幅曲率半径R对超压艇筋间囊体最大应力区均值的影响，得到了预测度较好的二阶模型；根据结构加强筋质量与加强筋间距L和筋直径d的关系，建立加强筋质量比例系数α与L和d的二阶模型，并建立了超压艇结构优化数学模型；针对不同加强筋质量比例系数，利用优化模型对结构设计参数进行优化，当加筋质量比例系数为30%时，可以获得较优的结果。