双向多轨迹判定方法在目标跟踪中的应用研究

李 孟 庭

(广东外语外贸大学 广东 广州 510420)



双向多轨迹判定方法在目标跟踪中的应用研究

李 孟 庭

(广东外语外贸大学 广东 广州 510420)

针对视频跟踪中存在的目标飘移问题，提出基于双向多轨迹判定的跟踪方法。首先，在一定时间间隔中分别使用纹理、颜色，以及光照不变量特征的三种组件跟踪器，对目标进行正向跟踪。然后，以正向跟踪结果作为初始位置，进行相应反向跟踪。通过分析成对正向反向轨迹，提取几何相似性、循环量和外观相似性，并计算各跟踪器轨迹准确性分数。最后，选择准确性分数最高的跟踪器的正向跟踪轨迹作为最终的跟踪结果。实验结果表明：与几种传统跟踪方法相比，提出的双向多轨迹判定跟踪方法通过融合不同的特征信息，跟踪性能显著提升。

目标跟踪 反向跟踪 双向多轨迹判定 几何相似性

0 引 言

近年来，视频目标跟踪在人们的生活中得到广泛应用，为此提出了大量视频跟踪算法[1-2]。大多数跟踪算法均由于不同原因遇到目标飘移问题，包括特征描述符辨识力低、遮挡、光照突变等[3]。为了达到更稳定准确地跟踪目的，如何克服目标飘移问题成为研究的热点。

由于不同特征描述符，表达不同的信息，所以某种特定的特征类型不能完全从视频背景中辨别出跟踪目标[4-5]。如文献[4]提出了一种自适应特征融合AFF(Adaptive Feature Fusion)的鲁棒跟踪方法，通过比较多种跟踪器的跟踪位置，估算目标的大体位置；然后，使用估算出位置的信息更新所有跟踪器。然而，如果多种跟踪器由于干扰无法找到某一帧中跟踪目标的位置，那么错误跟踪会延伸到剩余的帧中。其他自适应方法，有自适应稀疏表达ASR(Adaptive Sparse Representation)跟踪方法[6]和自适应实时压缩ARTC(Adaptive Real-Time Compressive)跟踪方法[7]。ASR[6]主要是为了克服光照和阴影变化，目标采用稀疏表达模板；ARTC[7]的自适应主要体现在参数学习的自适应。然而，这两种方法在复杂背景下进行目标跟踪，目标容易发生漂移现象。

为解决错误延伸问题，文献[8-10]提出了有记忆的跟踪系统，这种跟踪系统可以提炼跟踪器的轨迹。如文献[8]提出一种基于人类记忆模型HMM(Human Memory Model)的跟踪方法，HMM[8]长期跟踪器能够储存每一帧中目标的可能位置，用动态规划估算跟踪目标的轨迹，这样可以考虑到位置的置信度和连续帧中位置之间的时序关系。然而，有记忆的跟踪器采用了固定特征描述符，这些描述符不能有效地将跟踪目标从一些序列的背景中分离出来。

基于学习的跟踪器运用非常广泛，如文献[11]的STRUCK跟踪器，采用SVM判别式函数，将学习与跟踪结合在一起，有效避免了样本标记的不明确性，本文组件跟踪也采用了STRUCK[11]。文献[12]提出一种基于王-朗蒙特卡洛MLMC(W-L Monte Carlo)的跟踪方法，将新的抽样方法融入到蒙特卡洛跟踪框架，缓解了运动平滑约束和跟踪的突然运动。为了增加学习的鲁棒性，文献[13]提出了多高斯不确定性MGU(Multiple Gaussian Uncertainty)方法。根据在线学习框架的局部运动，提高跟踪的鲁棒性。

本文提出了一种新的双向多轨迹判定跟踪算法BMPD(Bidirectional Multiple Trajectory Determination)，其将“多种跟踪器的跟踪”和“有记忆的跟踪”结合起来。采用了三种使用不同特征的正向跟踪器，它们分别基于纹理信息、颜色信息和光照不变量信息。通过计算三种跟踪器的准确性分数(几何相似性、循环量和外观相似性)，选出最佳跟踪结果。本文的主要工作为：

(1) 采用新型多轨迹判定方法从多种跟踪器中提取最佳轨迹。

(2) 基于几何相似性、循环量和外观相似性定义成对正向和反向轨迹的准确性分数。

1 STRUCK跟踪器

该部分对STRUCK跟踪器原理进行简要介绍[11]。假定X表示跟踪目标的跟踪框位置，d表示跟踪框从先前帧移到当前帧的位移矢量。STRUCK使用了形式为f(x,d)=wtφ(x,d)的判别式函数，其中φ(x,d)是x和d的联合特征图，w是超平面的标准矢量。判别式函数可以简化为：

(1)

式中，x(i)和d(j)是支持矢量，k(·)是用于将线性分类器转换为非线性的联合基函数。β(i,j)>0是正支持矢量，β(i,j)<0是负支持矢量。

(2)

估算xt之后，从帧t中生成标记好的训练样本，并将其利用实时SVM算法更新判别式函数。STRUCK跟踪器采用有结构的SVM分类器，将学习与跟踪很好地结合起来，避免了样本标记中的不明确性。

2 双向多轨迹判定方法

当跟踪目标改变其外观或跟踪目标被其他物体遮挡时，跟踪就会失败。这种外观改变很难从目标外观的自身变化中辨别出来。为了克服这一难题，本文提出的双向多轨迹判定跟踪器，采用了反向跟踪器，它能在相反的时间顺序中检测出某一特定目标。通过比较反向轨迹与正向轨迹，可以判定正向跟踪器检测是否正确。此外，还采用了多种正向跟踪器，能提供多种轨迹假设。基于正向和反向分析，选出最佳正向轨迹，以提升跟踪的精准性和鲁棒性。

2.1 组件跟踪器

本文采用了三种组件跟踪器：Γ1、Γ2、Γ3，其均基于STRUCK跟踪器。这些跟踪器使用不同的特征描述符，并独立确定目标轨迹。其特征表示符分别如下所述：

Γ1：第一种跟踪器使用Haar-like特征来表示跟踪目标的纹理特征[6]。Haar-like特征的包围盒被分为4×4块，每块中包含六种不同类型的特征，特征矢量的维度为192，矢量中的所有元素的范围均为[-1,1]。

Γ2：第二种跟踪器使用颜色直方图来表示跟踪目标的局部颜色分布。包围盒也被分为4×4块，从每块中提取48个色彩空间的颜色直方图。该特征矢量的维度为768。

Γ3：第三种跟踪器采用光照不变特征。首先，从L通道图像中获得图像梯度幅值。随后，从幅值中获取累积直方图。通过使用累积直方图，将幅值图像转化为等级图像，其中每个幅值都用相应的累积直方图的值来代替。将单级图像与三通道色彩空间图像整合成一种四通道图像。最后，将四通道包围盒进行空间下采样变为16×16块，以获得1 024维的特征矢量。

为测量特征矢量u和v的相似性，本文使用交叉核将其结合起来，如式(3)所示：

(3)

式中，D表示特征维度。

2.2 准确性测量

三种组件跟踪器，生成了三种跟踪轨迹。本文测量每种跟踪器的准确性，并选出最稳健的跟踪器的轨迹结果作为最终轨迹。本节对跟踪器的准确性测量方法进行详细描述。

(4)

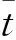
(5)

本文通过三种测量标准(几何相似性、循环量和外观相似性)来检验正向轨迹的可靠性。首先，帧t的几何相似性gt定义如式(6)所示：

(6)

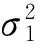
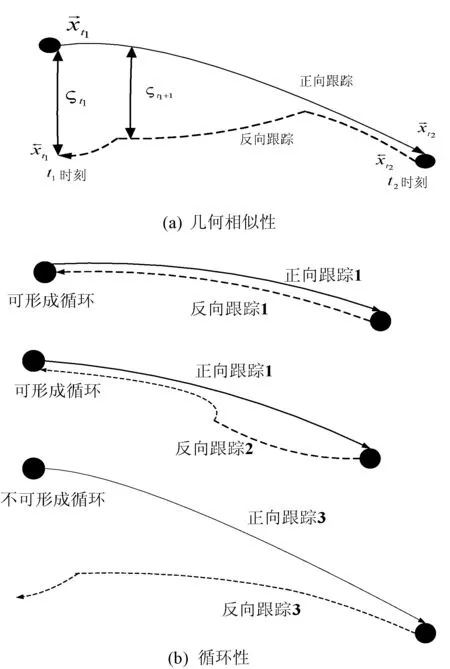
图1 轨迹分析

为了评价该种情况，本文首先计算两种相对应包围盒的重叠比ζt，如式(7)所示：

(7)

(8)

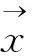
(9)

最后，本文结合几何相似性、循环量和外观相似性来确定在[t1,t2]期间跟踪器的准确性，如式(10)所示：

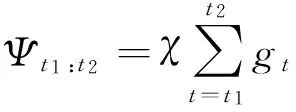
(10)

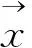
2.3 通过最优轨迹选择跟踪

本文通过分析多种跟踪器获得的成对正向反向轨迹实现跟踪。为了减轻计算成本，本文对连续τ帧的集合进行了轨迹分析，两个连续集共享一个边界帧。即间隔[t-τ,t]的轨迹分析和下一个间隔[t,t+τ]的轨迹分析共享帧t。因此，轨迹分析路径只能分析τ的倍数的帧。

本文首先利用组件跟踪器Γ1、Γ2、Γ3对间隔[t-τ,t]进行分析，得到三个正向轨迹和相应的反向轨迹。然后，利用式(10)计算三种跟踪器的准确性分值，选出分值最高的跟踪器为最优跟踪器。定义式(11) 表示最优跟踪器的正向轨迹，并将其视为最终跟踪结果。

(11)

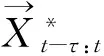
当有非目标物体在目标物体附近时，不能在短期间隔τ中有效地选出最优跟踪器。此时应增大间隔，保证能从目标物体中将非目标物体分离出来。但是另一方面，间隔τ较长时，某次错误跟踪的影响就会更加严重。因此，选择合适的τ显得重要。不同τ情况下平均成功率ASR(Average Success Rate)和平均准确率AAR(Average Accuracy Rate)的曲线如图2所示，其中ASR表示识别成功时的曲线区域，AAR表示正确帧的百分比[14]，这些帧中目标的真实位置在20个像素内。可以看出，当τ=30时，ASR和AAR有最大值。因此本文取τ为30。

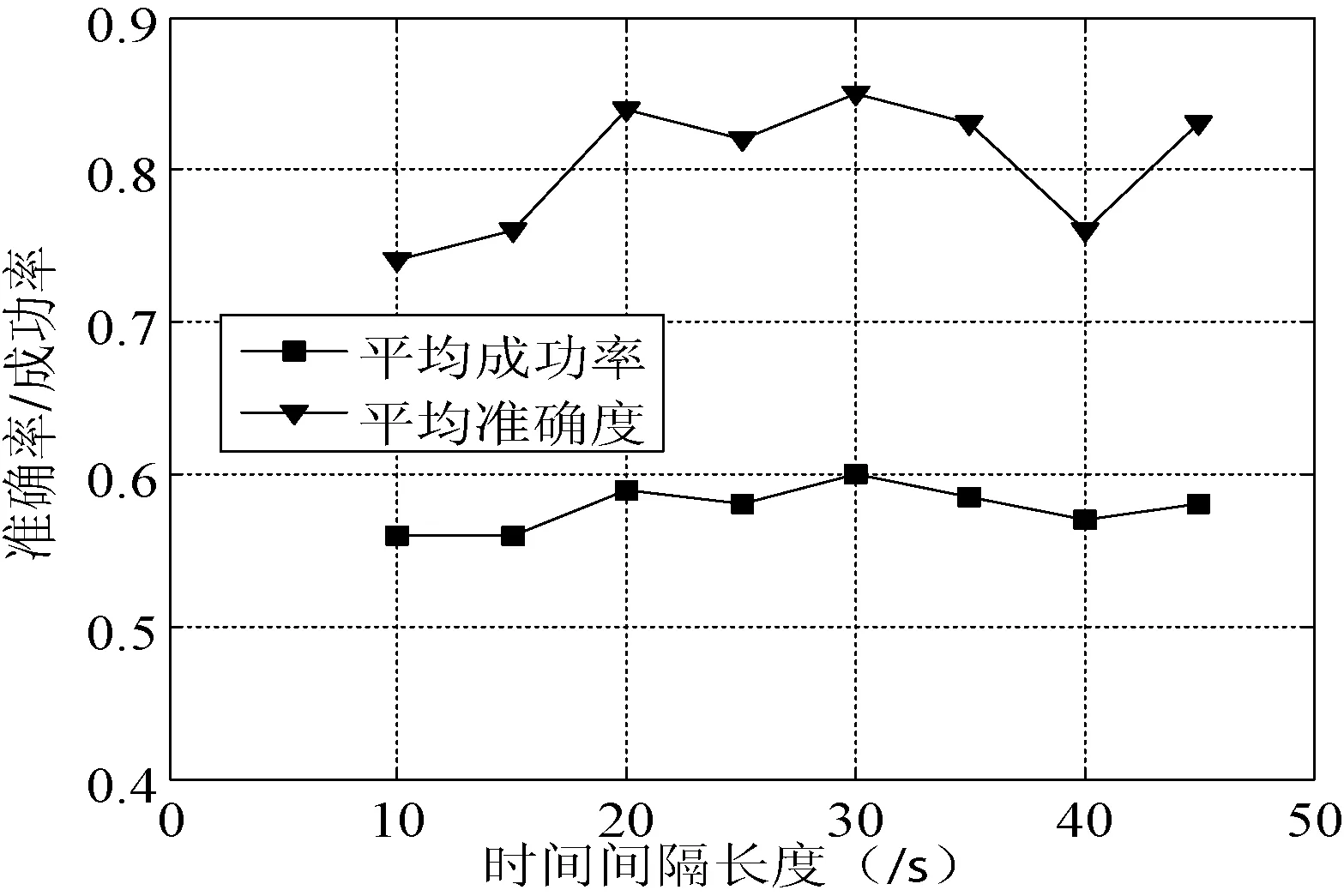
图2 不同τ情况下ASR和AAR结果

2.4 错误处理

当式(8)中最优跟踪器的循环量χ为1时，当前间隔[t-τ,t]中就出现了跟踪错误。当所有组件跟踪器在连续帧中gtφt≤δ2长达2/3τ时，也可以判定跟踪错误。本文中δ2=0.004。当检测到跟踪错误时，本文就不更新所有组件跟踪器的分类器。同时，发生跟踪错误时，目标有可能会超出正常搜索范围。因此，本文将搜索范围从R扩大至4×R，但是在已增加的搜索范围内从每64个样本中检查一个样本，以降低计算复杂性。

3 实验结果及分析

本文利用基准数据集[15]测试所提出的双向多轨迹判定算法的性能，该数据集中包含在复杂背景下的测试序列，如光照变量、遮挡等情形。实验分为两个部分，为了验证本文算法多特征轨迹判定的优势，对不同特征轨迹组合的结果进行比较；同时，为了验证本文算法的性能，与其他传统的跟踪方法进行比较。

3.1 不同特征轨迹比较

本部分实验中，不同特征轨迹组合的跟踪方法的ASR和AAR结果如表1所示。其中BMPD表示使用了所有组件跟踪器Γ1、Γ2、Γ3，BMPDi表示只使用了一种跟踪器Γi(i=1,2,3)，BMPDi,j表示使用了两种跟踪器Γi和Γj(i=1,2,3;j=1,2,3)。本文测试了每一种可能的结合。当只采用一种跟踪器时，BMPD2采用颜色特征的Γ2跟踪器，其跟踪结果比其他两种跟踪器更精准。当联合使用两种跟踪器时，BMPD2,3的效果较好。但通过联合三种跟踪器Γ1、Γ2、Γ3，BMPD的结果最佳。所以，本文提出的多轨迹判定方法，通过融合不同的特征信息，可进一步提高跟踪准确性。

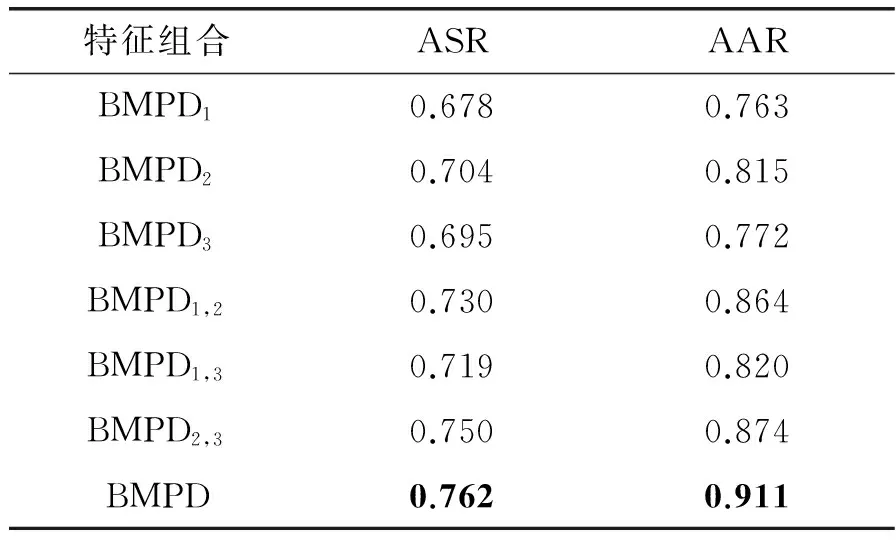
表1 不同特征组合方法的ASR和AAR结果

3.2 不同算法比较

为了进一步验证本文BMPD算法的有效性，将BMPD方法与7种跟踪器方法进行比较：AFF[4]、ASR[6]、ARTC[7]、HMM[8]、STRUCK[11]、WLMC[12]和MGU[13]。如表2所示。

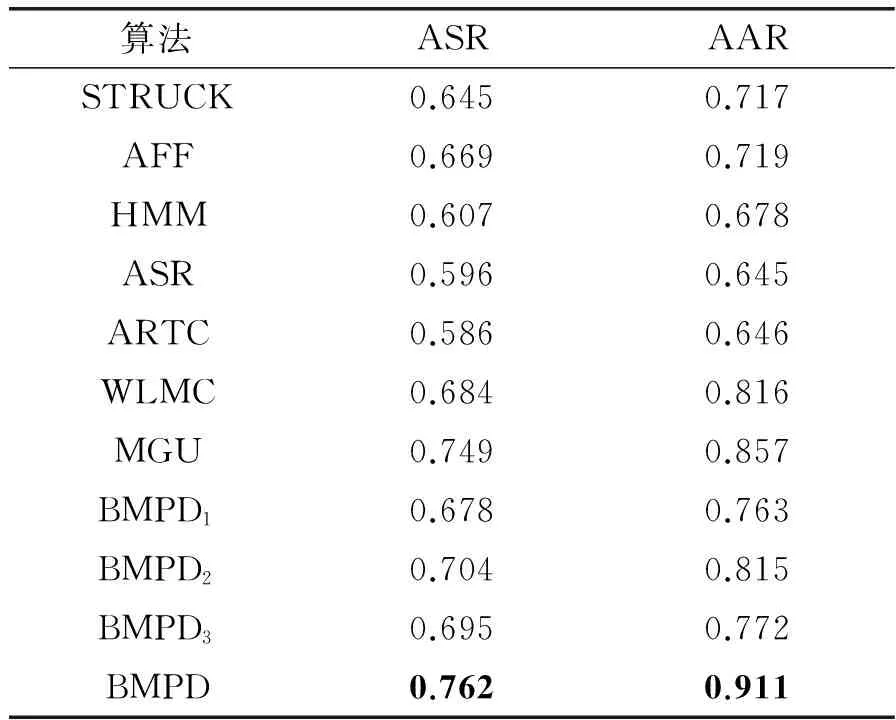
表2 各算法ASR与AAR比较结果

表2给出各种算法的ASR和AAR的结果。与表1一样，最后四行与本文提出算法相对应：BMPD使用了所有组件分类器，BMPDi表示只使用了一种分类器Γi(i=1,2,3)。该四种方法均利用2.4节的错误处理方法以抑制跟踪错误的延伸，各组件分类器均基于STRUCK，其中粗体字表示最佳结果。

可以看出，即使只使用了单一组件跟踪器，由于添加了跟踪错误处理器，所提算法优于传统的STRUCK方法。此外，本文的双向多轨迹判定方法BMPD的性能优于其他所有传统算法，其ASR和AAR结果分别比STRUCK高出11.7%和19.4%。

为了进一步分析验证本文方法的有效性，利用各种跟踪方法对常见的几组非基准测试序列进行比较。其中非基准测试序列来自文献[12]。对于不同测试序列，各算法的ASR和AAR结果如表3所示。可以看出，本文提出的BMPD方法具有最佳的跟踪效果。ASR和AAR的平均值分别比STRUCK方法高出28%和42%，比MGU方法高出11%和12%。

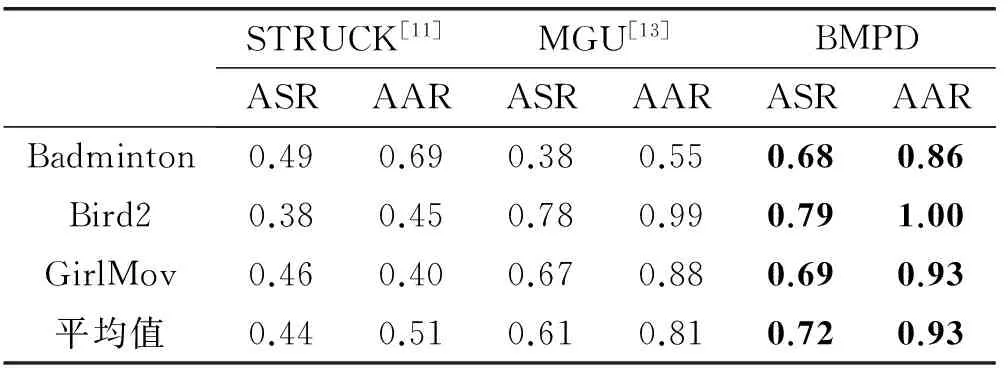
表3 对于非基准序列各算法的跟踪结果

4 结 语

本文提出双向多轨迹判定跟踪器对视图进行跟踪，使用了三种组件跟踪器。在指定时间间隔内，每个组件跟踪器均计算正向轨迹和反向轨迹；通过分析正向和反向轨迹，提取几何相似性、循环量和外观相似性，并将它们联合起来定义跟踪器的准确性分数；选出准确性分数最高的跟踪器的正向跟踪轨迹作为最优跟踪结果；如果各组件跟踪器的准确性分数均较低，则进行错误处理，抑制错误累积情况。通过在基准测试序列和非基准测试序列的实验，结果表明，本文提出的BMTD方法比传统跟踪器具有更准确的效果。

本文使用的三种跟踪器均是基于STRUCK[11]的组件跟踪器。将来的研究方向可将多轨迹判定应用到其他组件跟踪器中，并且使用更多的特征跟踪器进行判定，进一步提高跟踪准确性。

[1] 王保宪.复杂背景下的视频目标跟踪算法研究[D].北京:北京理工大学,2016.

[2] 刘定通.复杂背景下视频运动目标检测与跟踪算法研究[D].成都:电子科技大学,2016.

[3] Djamal M,Rabah Iguernaissi,Kheir E A,et al.Tracking Multiple Persons under Partial and Global Occlusions:Application to Customers’ Behavior Analysis[J].Pattern Recognition Letters,2016,81(10):11-20.

[4] 郇二洋,李睿.基于自适应特征融合的粒子滤波目标跟踪算法[J].计算机科学,2015,42(2):316-318.

[5] 李维维,张陈斌,陈宗海,等.基于特征学习与体征记忆模块更新机制的粒子滤波跟踪[J].中国科学技术大学学报,2014,44(4):292-302.

[6] Nhat V Q,Lee G.Illumination Invariant Object Tracking with Adaptive Sparse Representation[J].International Journal of Control Automation and Systems,2014,12(1):195-201.

[7] Zhang W Z,Ji J G,Jing W F,et al.Adaptive Real-Time Compressive Tracking [C]//IEEE International Conference on Network and Information Systems for computers,2015,9:236-240.

[8] 齐玉娟,王延江.基于人类记忆模型的粒子滤波鲁棒性目标跟踪算法[J].模式识别与人工智能,2012,25(5):810-816.

[9] 郭强,孙鹏,赵迎春,等.基于记忆梯度追踪的高效稀疏跟踪算法[J].计算机辅助设计与图形学学报,2016,28(4):565-572.

[10] 吴世东.基于视觉显著性的粒子滤波跟踪算法研究[D].北京:中国科学技术大学,2015.

[11] Hare S,Golodetz S,Saffari A,et al.Struck: Structured Output Tracking with Kernels[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2015,23(5):263-270.

[12] Kwon J,Lee K M.Wang-Landau Monte Carlo-based tracking methods for abrupt motions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(4):1011-1024.

[13] Zhang B,Perina A,Li Z,et al.Bounding Multiple Gaussians Uncertainty with Application to Object Tracking[J].International Journal of Computer Vision,2016,118(3):364-379.

[14] Wu Y,Lim J,Yang M H.Online Object Tracking:A Benchmark[C]//IEEE Conference on Computer Vision and Pattern Recognition,2013:2411-2418.

[15] Zhang W Z,Ji J G,Jing W F,et al.Adaptive Real-Time Compressive Tracking[C]//IEEE International Conference on Network and Information Systems for computers,2015,9:236-240.

APPLICATION OF BIDIRECTIONAL MULTIPLE TRAJECTORY DETERMINATION IN OBJECT TRACKING

Li Mengting

(GuangdongUniversityofForeignStudies,Guangzhou510420,Guangdong,China)

Regarding the problem that most tracking algorithms experience object drift, we proposed a new tracking method based on bidirectional multiple trajectory determination. Firstly, we used the three component trackers of texture, color, and illumination invariant characteristics in a certain time interval to track the target forward. Then, we took the results of forward trace as the initial location to perform a corresponding reverse trace. After that, we extracted geometric similarity, the circulation volume, the appearance similarity, and calculate the tracker accuracy score of each tracker by analyzing the forward and backward trajectories. Finally, the forward tracking trajectory of the tracker with the highest accuracy score was selected as the final tracking result. Compared with traditional tracking methods, the experimental results show the proposed bidirectional multiple trajectory determination method improves the tracking accuracy through fusing different features.

Object tracking Backward tracking Bidirectional multiple trajectory determination Geometry similarity

2016-10-26。广东省科技厅软科学项目(2015A070704053)；广东外语外贸大学大学生创新训练计划项目(2016 11846068)。李孟庭，讲师，主研领域：多媒体技术，图像处理，管理智能化。

TP391

A

10.3969/j.issn.1000-386x.2017.07.026