一种提高测角精度的线交叉寻峰算法
2020-07-23田孝华刘小虎赵颖辉
田孝华,刘小虎,赵颖辉,何 晶,邹 鲲
(1.西安培华学院智能科学与信息工程学院,陕西 西安 710125;2.空军工程大学信息与导航学院,陕西 西安 710077)
0 引言
通过测量2个脉冲的时间间隔来测量距离、角度等参量在工程上有着广泛应用,如测距器、微波着陆系统以及雷达就是典型案例[1]。在这种测量方法中,脉冲时间间隔测量的准确性直接影响参量的测量精度,且参量测量误差与时间间隔测量误差呈线性关系,如何高精度测量时间间隔一直是工程实现中需要解决的问题。
行业性质:绝大多数企业位于产业链利润最低的制造环节:超过90%的企业均为生产型企业;占据产业链高端环节的企业很少:总部、研发设计、采购及业务等比例较小,占比最大的采购环节亦仅五分之一左右。
研究人员针对此问题进行了深入研究,取得的成果可分为2大类,即传统测量技术的改进方法与基于现代数字信号处理技术的改进方法。考虑到传统的时间间隔测量通常为2个步骤:第1步找出测量参考点;第2步采用脉冲计数的方式测量2个参考点的时间间隔。因此,在传统测量技术的改进方法中,主要是通过设计脉冲的形状提高参考点的准确性,提高计数脉冲的频率减小计数脉冲导致的误差。常用的有钟形脉冲与矩形脉冲,但有限的系统带宽会导致矩形脉冲波形失真,而钟形脉冲无论选择半幅度点、半功率点,还是峰值点作为参考点,在低信噪比条件下准确性均会受到影响。通过提高计数脉冲的频率虽然可以减小计数脉冲带来的误差,但无法消除。可见,传统测量技术的改进方法很难满足高精度测量设备要求[1-3]。随着现代电子实现技术与数字信号处理技术的发展,采用现代数字信号处理技术改进时间间隔测量精度成为可能。文献[4-6]分别针对三角波与正弦波采用内插采样技术提高测量精度,文献[7-8]通过相位测量得到高精度的时间间隔值,文献[9-11]提出了基于二次相关技术的参数测量方法,文献[12-14]采用曲线拟合技术改善测量精度。除此之外,还提出了分层次测量方法[15]、三点寻峰算法[16]等。以上基于现代数字信号处理技术改进方法的优点是利用所有采样数据改善测量精度,克服了传统测量方法仅利用某一点(半幅度点、半功率点,峰值点)的值作为参考值而易受噪声影响的问题,其不足之处是或者对波形形状有要求,或者波形的持续时间对测量精度有影响,或者不适用于工程广泛使用的钟形脉冲波形,应用场合受到限制。
本文针对高精度时间间隔测量问题展开研究,提出了一种适用于前后沿对称脉冲波形的线交叉寻峰算法,并采用计算机对该方法进行了仿真分析,针对该方法利用所有采集数据改善测量精度方面与传统方法做分析和比较,来验证该方法的有效性和实用性。
1 线交叉寻峰算法
设以采样率fs(采样间隔Ts=1/fs)对脉冲进行AD转换,脉冲波形上第1个采样点数据为x(0),脉冲波形上共采样N个数据,用x(0),x(1),…,x(N-1)表示,不同采样率条件下采样数据在脉冲波形上的分布如图1所示。采样点是分布在脉冲波形的前沿还是后沿可根据脉冲波形的宽度、采样率以及相邻数据的大小来判断,在脉冲波形宽度与采样率确定的条件下,前、后沿的采样点数或者相等,或者相差为1。线交叉寻峰算法依据采样数据x(n)实现对真实峰值点的估计,即估计采样的峰值点偏离真实峰值点的误差Δt。下面分几种情况讨论本文提出的线交叉寻峰算法。
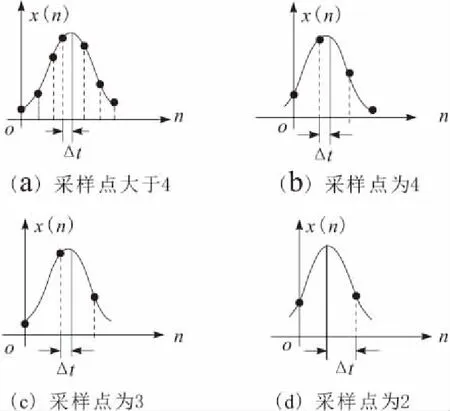
图1 不同采样率条件下采样数据在脉冲波形上的分布
1.1 脉冲波形采样点数大于4
脉冲波形采样点数大于4的情况如图1a所示,设在脉冲波形上共采样N个数据,其中脉冲前沿P个数据,后沿N-P个数据,则线交叉寻峰算法如下。
式中,〡·〡表示取绝对值,(·,·)max表示取最大值。
脉冲波形采样点数等于4的情况如图1b所示,线交叉寻峰算法如下。
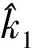
(1)
x=(x(0),x(1),…,x(P-1))T
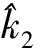
工程实施规模化管理后,灌溉时农民只需在田间接1~2节软带即可,省去梯级灌溉提水设备搬运、铺设管路等费时、费工的工序,避免了管路接头漏水、阻水和接头断开等现象,灌溉时既省时、省力、又省钱,节省出的时间可以从事其他工作。灌溉工程建成后,明显缩短灌溉时间,保证作物各生长期的适时灌溉,果品可增产15%以上;对于一些输水距离较远、灌溉困难的地块,果农以往都很少进行灌溉,铺设管路后,灌溉得到了保证,果品增产可达50%以上,效益更加可观。灌溉工程提高了灌溉水利用率,每亩每年节水31.5 m3,在节水的同时每亩每年节省柴油2.74 L。
(2)
由脉冲前沿的2个采样点x(0)与x(1)可建立线性关系式(7)。利用脉冲前、后沿波形的对称性,建立与后沿波形对应的线性关系为
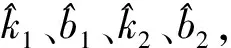
盛茂产[19]认为,包世臣书学理论的主要特色是大力提倡北碑以矫宋、明以来临攀阁帖的风气,至于其不足在于提倡碑版、力求改革时弊的理论中,也有矫枉过正、语过其实之处,他推崇北碑书法,而其在碑版书法方面的成就并不卓著。
(3)
峰值点对应的时间为
(4)
估计的峰值点对应时间t与前沿的x(1)对应时间偏差为
Δt=t-(P-1)Ts
(5)
估计的峰值点对应时间t与后沿的x(P)点对应时间偏差为
Δt′=PTs-t
(6)
1.2 脉冲波形采样点数等于4
鉴于英语学习的特殊性,教师要鼓励每一个学生参与学习,并力争学有所获。因此教师要学会因材施教。要克服传统英语教学的弊端,即只顾传授知识,解决难题,很少顾及学生的感受。要在听、说、读、写的训练中考虑学生的接受能力,多鼓励,少批评,让每个孩子都能跟上学习的节奏,寓教于乐,在轻松的氛围中完成学习。
由脉冲前沿的2个采样点x(0)与x(1),建立如下线性关系
(7)
由脉冲后沿的2个采样点x(2)与x(3),建立如下线性关系
(8)
由式(7)与式(8)联立求解,可得峰值点对应的时间t。
估计的峰值点对应时间t与前沿的x(1)对应时间偏差为
(9)
估计的峰值点对应时间t与后沿的x(2)对应时间偏差为
(10)
1.3 脉冲波形采样点数等于3
脉冲波形采样点数等于3的情况如图1c所示,由于采样起始点的随机性,脉冲波形上采样的3个点可能是前沿2个、后沿1个,也可能是前沿1个、后沿2个,可依据3个采样值的大小来判断。即:若x(0)最小,x(1)最大,则脉冲前沿有2个点,如图1c所示;若x(1)最大,x(2)最小,则脉冲后沿有2个点。脉冲前沿有2个采样点的线交叉寻峰算法如下。
x′=(x(P),x(P+1),…,x(N-1))T
尽管健康与养生旅游在实践中获得了较快的发展,也越来越受到学术界的重视,但是与之相关的学术研究尤其是解释型研究还很缺乏。已有的相关文献多为描述型研究,主要关注健康旅游的供给或需求方面的某些特征(Huang &Xu,2018),缺乏视角创新和理论贡献。很少有研究关注游客如何通过旅游改善其健康状况,即旅游促进游客身心健康的机制尚不明晰。
(11)
由式(7)与式(11)联立求解,可得峰值点对应的时间t。
当然,以上实证最主要的结果在于验证了前文的假设,即适宜金融结构可通过技术进步对产业结构升级产生正向作用,且技术创新和技术转移在金融结构影响产业结构升级的传导途径中起到不同的作用。
(12)
估计的峰值点对应时间t与前沿的x(P-1)点对应时间偏差为
(13)
对于脉冲前沿有1个采样点,后沿有2个采样点的情况,采用相同方法可计算峰值点对应时间为
(14)
估计的峰值点对应时间t与后沿的x(1)对应时间偏差为
(15)
1.4 脉冲波形采样点数等于2
b.在数据x(n)中分别寻找往扫脉冲与返扫脉冲的最大值,并计算2个最大值之间的采样点数N,对往、返扫描脉冲时间间隔利用式(17)进行粗步估计。
(16)
2008年,在超薄卡片机等消费相机领域春风得意的索尼于当年9月推出了其首部全画幅单反产品A900,这台相机的上市价格达到了19000元左右。A900的问世使得全画幅单反相机产品线从两国争斗,变成了三分天下的局面。
1.5 线交叉寻峰算法估计往返扫描脉冲时间间隔
线交叉寻峰算法估计往返扫描脉冲时间间隔步骤如下:
a.对信号进行模数转换,获取数据x(n)。
脉冲波形采样点数等于2的情况如图1d所示,脉冲前沿与后沿各有1个采样点,分别用x(0)和x(1)表示,可用2个点在幅值上的差异进行峰值位置的修正。在本文提出的算法中,采用式(16)修正估计的峰值点对应时间t与两点的最大值对应时间的偏差。
δtr=(N+1)Ts
(17)
式中,Ts为采样周期。
(3)验证氯气是否具有漂白性,要对比验证干燥氯气和湿润氯气有无漂白性,因此Ⅰ处应为湿润的有色布条,Ⅱ处应为干燥剂,Ⅲ处应为干燥的有色布条,U形管中应用固体干燥剂。
c.利用线交叉寻峰算法对粗估的往、返扫描时间间隔进行修正,得到精确估计。首先,由采样率、脉冲波形宽度确定每个脉冲波形上的采样点数,由往扫脉冲与返扫脉冲的最大值以及与最大值相邻的数据大小确定采样的最大值是分布在脉冲的前沿还是后沿。其次,精确估计方法为
δtp=δtr±Δt1±Δt2
(18)
δtp和δtr分别为时间间隔的精确估计与粗步估计。±Δt1为对往扫脉冲最大值对应时间的修正值:若采样得到的往扫脉冲的最大值分布在脉冲前沿,则修正值为-Δt1,Δt1根据脉冲波形上采样点数选择式(5)、式(9)、式(13)以及式(16)的其中之一计算;若采样得到的往扫脉冲的最大值分布在脉冲后沿,则修正值为+Δt1,Δt1根据脉冲波形上采样点数选择式(6)、式(10)、式(15)以及式(16)的其中之一计算。±Δt2为对返扫脉冲最大值对应时间的修正值:若采样得到的返扫脉冲的最大值分布在脉冲前沿,则修正值为+Δt2,Δt2根据脉冲波形上采样点数选择式(5)、式(9)、式(13)以及式(16)的其中之一计算;若采样得到的返扫脉冲的最大值分布在脉冲后沿,则修正值为-Δt2,Δt2根据脉冲波形上采样点数选择式(6)、式(10)、式(15)以及式(16)的其中之一计算。
湖北传媒摄影技师学院副院长、Adobe认证讲师,在大陆及港台地区出版摄影类图书20余本,策划影展数十场。
2 计算机仿真分析
为了验证本文所提出方法的有效性,采用计算机进行了仿真分析。仿真环境为:假设脉冲为前后沿对称的钟形脉冲,脉冲宽度为200 μs。脉冲信号经AD转换以及二阶巴特沃斯数字低通滤波器(对应模拟低通滤波器的通带-3 dB频率为26 kHz)滤波后,进行峰值估计。仿真曲线的每个点由500次蒙特卡洛实验得到。
信息技术必将为幼儿教育带来新的途径与方法,具有积极的作用。灵活根据教学内容使用信息技术,必然能够给幼儿带来更好的学习体验,达到理想的效果。本文提出以下几项信息技术在农村幼儿园教学中的灵活应用措施。
本文主要仿真分析了以采样数为参变量,本文提出的方法所估计峰值对应时间的均方根误差与输入信噪比的关系,并与传统方法进行了性能比较。这里的传统方法指工程上常用的直接从采样数据中寻找最大值,并以此位置作为脉冲峰值所在位置的方法。首先,仿真分析了脉冲上采样点数大于4时算法的性能。当采样率分别为100 kHz(采样数为20)、50 kHz(采样数为10)时,均方根误差与输入信噪比的关系如图2所示,其中实线对应传统方法,虚线对应本文的线交叉寻峰方法。由图2可知:在采样数大于4时,采样率越高,测量精度越高;相对于传统方法,本文方法精度提高1倍左右;2种方法的输入信噪比越高,精度越高,且当信噪比小于0 dB时,测量精度受噪声影响较大,而大于0 dB时主要由采样率决定。
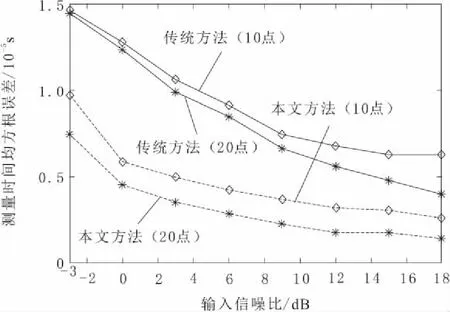
图2 采样点数大于4时,均方根误差与输入信噪比的关系
其次,仿真分析了采样点数小于等于4时算法的性能。当采样率分别为20 kHz(采样数为4)、14.3 kHz(采样数为3)、10 kHz(采样数为2)时,均方根误差与输入信噪比的关系如图3所示。由图3可知,除了能得到与上述类似的结论外,当采样点数为3和4时,传统方法误差相差不大,而本文方法采样点数为3的性能略优于点数为4的性能,这说明对于前后沿对称的波形来说,用一个沿的2点确定的直线斜率按对称性去推算另一个沿的斜率,比直接用4个点各自计算前后沿斜率来寻峰更为有效。
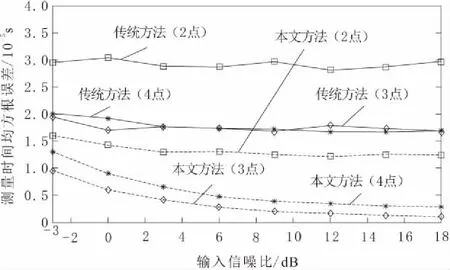
图3 采样点数为2、3、4时,均方根误差与信噪比的关系
3 结束语
本文提出了一种提高测角精度的线交叉寻峰算法,该方法适用于前后沿对称的脉冲波形。与传统方法相比,具有测量精度高、便于工程实现、对采样率要求不高的优点,通过计算机仿真验证了方法的有效性。该方法不仅适用于微波着陆系统的角度测量,还适用于对脉冲峰值位置需要进行准确估计的场合,如精密测距器、塔康以及其他高精度测试设备等。
