常见的几个抽象函数问题及其求解策略
2020-07-22杜红全
杜红全
(甘肃省康县教育局教研室 746500)
抽象函数是相对个体的函数而言的,是指没有给出具体的函数解析式或对应关系,只是给出函数所满足的一些条件或性质的一类函数.抽象函数问题一般是由所给的条件或性质,讨论函数的其他性质,下面举例说明.
一、根据条件等式求解析式
例1已知3f(x)+2f(-x)=x+3,求f(x).
分析x,-x同时使得f(x)有意义,用-x代替x建立关于f(x),f(-x)的两个方程即可求得f(x).
解因为3f(x)+2f(-x)=x+3, ①
用-x代替x,得3f(-x)+2f(x)=-x+3. ②
点评求解本题的策略是利用方程消元法,所谓方程消元法就是指利用方程组通过消参、消元的途径达到求函数解析式的目的.
二、求抽象函数的值
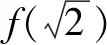
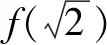

点评本题求值策略是利用迭代法. 求抽象函数的值还有赋值法、代换法等.
三、求抽象函数的定义域


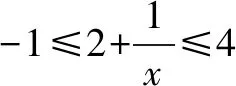
点评求抽象函数的定义域的策略是利用函数的概念,即由f(x)的定义域[a,b],求f[g(x)]的定义域的方法:由a≤g(x)≤b,求出x的取值范围,即为函数y=f[g(x)]的定义域;由f[g(x)]的定义域[a,b],求f(x)的定义域的方法:由a≤x≤b,求出g(x)的取值范围即可,即与由f(x)的定义域[a,b],求y=f[g(x)]的定义域恰好相反.
四、求抽象函数的值域

分析利用换元法求解.

点评求解本题的策略是利用换元法,但必须把新元的取值范围弄清楚.
五、求抽象函数单调区间
例5 若函数f(x)在(-,+)上是减函数,求函数f(2x-x2)单调递增区间.
分析用复合函数的单调性来求.
解因为f(x)在(-,+)上是减函数,所以f(2x-x2)单调递增区间应是u=2x-x2单调递减区间,又u=2x-x2的单调递减区间是[1,+),所以函数f(2x-x2)单调递增区间是[1,+).
点评求解本题的策略是利用复合函数单调性的求法.
六、比较抽象函数值的大小



点评求解本题的关键是把对应的两个变量的值转化到同一个单调区间内,求解策略是利用函数的单调性和转化思想.
七、抽象函数图象问题
例7 由函数y=f(x-1)的图象,通过怎样的图象变换可得函数y=f(-x+2)的图象.
分析解答此题须综合应用函数图象的变换的对称、平移变换.
解将函数y=f(x-1)的图象向左平移1个单位,得到函数y=f(x)的图象,将函数y=f(x)的图象沿y轴翻折,得到函数y=f(-x)的图象,将函数y=f(-x)的图象向右平移2个单位,就可以得到函数y=f(-x+2)的图象.
点评求解本题的策略是利用函数图象变换的规律.
八、解抽象不等式
例8 已知f(x)在(0,+)上单调递增,解不等式f(x)>f[8(x-2)].
分析求解本题的关键在于由f(x)>f[8(x-2)]去掉函数关系符号“f”,使抽象的不等式问题转化为具体不等式问题,注意函数的定义域也是一个限制条件.
解由f(x)>f[8(x-2)]和f(x)在(0,+)上是增函数,得解不等式组,得所以原不等式的解集为
点评单调性定义要能够逆用,f(x)是[a,b]上的增函数,则f(x1) 点评求解此类问题的策略是适当的赋值(代入特殊值). 例10 函数f(x)的定义域为R,且对任意x,y∈R,有f(x+y)=f(x)+f(y),又当x>0时,f(x)<0,f(1)=-2. (1)证明f(x)是奇函数; (2)证明f(x)在R上是减函数; (3)求f(x)在区间[-3,3]的最大值和最小值. 分析给出函数满足的条件关系式而未给出解析式,要证明函数的奇偶性与单调性,关键是紧扣条件f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,对其中的x,y不断赋值,根据f(x)在R上是减函数求出最值. 解(1)令y=-x,得f[x+(-x)]=f(x)+f(-x),所以f(x)+f(-x)=f(0).又因为f(0+0)=f(0)+f(0),所以f(0)=0,所以f(x)+f(-x)=0,即f(-x)=-f(x),所以f(x)是奇函数. (2)任取x1,x2∈R,且x1 (3)因为f(x)在R上是减函数,所以f(x)在区间[-3,3]上的最大值是f(-3),最小值是f(3).f(3)=f(1)+f(2)=3f(1)=3×(-2)=-6,所以f(-3)=-f(3)=6.从而f(x)在区间[-3,3]上的最大值是6,最小值是-6. 点评求解此类问题的策略是利用赋值法,即对抽象函数的奇偶性与单调性的证明,围绕证明奇偶性与单调性所需要的关系式,对所给的函数关系式赋值.九、证明等式


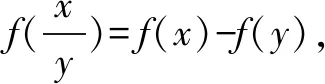
十、抽象函数的综合问题
