巧用“构造相似比”解向量与三角形的综合问题

谢玉平

(广西南宁市第二中学 530022)

相似三角形的一切对应线段(对应中线，对应高，对应角平分线，外接圆的半径，内切圆的半径)的比等于相似比.高考考查的平面向量和解斜三角形的综合题中变量之间的关系不好找，思维量和计算量都很大，学生往往很难得到正确结果，以至于很多学生直接放弃这一类型的考题.其实平面向量和斜三角形中的很多点都是一些特殊线段的交点，如果利用构造相似三角形借助相似比来解决这类问题，思维量和计算量都相对较小，可以实现化繁为简，一解服务多题的功效.

常用解法：解方程组法.

评析此题考查的是平面向量基本定理问题中确定基底系数的问题.既是高考考查的重点也是难点.用解方程组法解此题除了运算量大容易出错外，两个方程的构建也有一定的难度，理解不到位的学生可能两个方程都是用CM或者BN来表示，导致后面化简出来的等式是恒等式，解不出系数.

构造相似比法：

解过M作MH∥AN，交BN于H.

评析如果知道点E在线段CM上的具体位置，那么用向量加法和减法法则进行加减代换，就可以确定基底的系数了.点M，点N的位置是确定的，通过构造相似比可以求出点E是CM的一个等分点，即点E的位置可以确定.

变式1如图1，已知△ABC的面积为14cm2，D，E分别为边AB，BC上的点，且AD∶DB=BE∶EC=2∶1，AE，CD交于点P，则△APC的面积为____cm2.

构造相似比法.

过D作DH∥AE,交BC于H.

评析如果知道点P在线段CD上的具体位置，那么用向量加法和减法法则进行加减代换，就可以确定基底的系数了.点D，点E的位置是确定的，通过构造相似比便可以求出点P是线段CD上的几等分点.

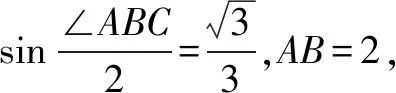
常见解法：利用余弦定理建立等量关系.

解cos∠ABC

设AC=3b,BC=a，在△ABC中由余弦定理可得:

在△DBA和△DBC中，

因为cos∠ADB=-cos∠BDC,

由余弦定理可得

所以3b2-a2=-6 ②.

由①②可得a=3,b=1,即BC=3.

评析此题考查的是解三角形问题.容易想到用余弦定理建立方程，但是在哪个三角形中使用余弦定理可能要进行一定的思考，三角形选择得不得当，运算量会增大，况且上面解法的运算量也不小.

构造相似比解法.

解cos∠ABC

设BC=x，在△BDE中由余弦定理有：BD2=BE2+DE2-2BE·DE·cos∠BED，

评析通过作平行线构造相似比，可以把题目中的三个已知条件同时放在△BDE中，建立方程的方向一目了然，大大降低了运算量和思维量.

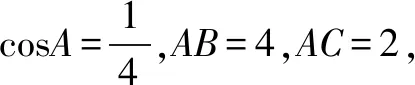
构造相似比解法.

过D作DH∥AB，交AC于H.在△ADH中由余弦定理有：

AD2=HA2+HD2-2HA·HD·cos∠AHD

评析通过作平行线构造相似比，把题目中的三个已知条件同时放在△ADH中，通过余弦定理可以直接求出AD长，简捷易算.