关于设点法解一类圆锥曲线问题的思考

李晖

（泉州第五中学，福建 泉州 362000）

解析几何的本质，就是用代数方法解决平面几何问题。高中数学中，解析几何模块对学生提出了比较综合的要求，也是高考对学生数学核心素养考查的重点和难点。在解决直线与圆锥曲线位置关系的问题中，通常有两种方法：设线法与设点法。教师在解几教学中，应注意解题方法的多中取精，着力培养学生总结优化方法和运算技巧的能力。

一、设线法与设点法的定义与适用场景介绍

所谓“设线法”，即以“线”为源头，设出直线方程，通过联立直线和圆锥曲线方程，利用方程思想，结合韦达定理解决问题［1］。利用这种方法可解决直线与圆锥曲线位置关系的许多问题：比如常见的求几何量的范围最值问题，定点定值问题等，是解析几何问题的常规解法。“设点法”，即以“点为源头”，设出曲线上点的坐标，利用点的坐标作为参数来解决问题，这种方法通常不需要联立直线与圆锥曲线的方程。比如涉及到弦的中点问题中常见的“点差法”就是“设点法”的典型。在近几年的高考中，大部分的圆锥曲线解答题都可以用设线法解决，但是也有一部分题目，用“设线法”计算量过大或者无法解决，设点法才是最优的解法。对“设线法”，学生经过长期的练习，都比较熟悉，难点主要在于应用数形结合对题目几何条件的代数转化，文章不再详述。

二、例举设点法在圆锥曲线教学的应用

对于设点法，学生通常比较陌生，什么情况下采用设点法，设点后又如何推进解题过程，笔者通过下面的例题进行分析。

例.已知抛物线Γ:y2=4x，经过点A(3,-2)的直线交抛物线Γ 于M,N两点，经过定点b(3,-6)和M的直线与抛物线Γ 交于另一点L，问直线NL是否恒过定点，如果过定点，求出该定点，否则说明理由。

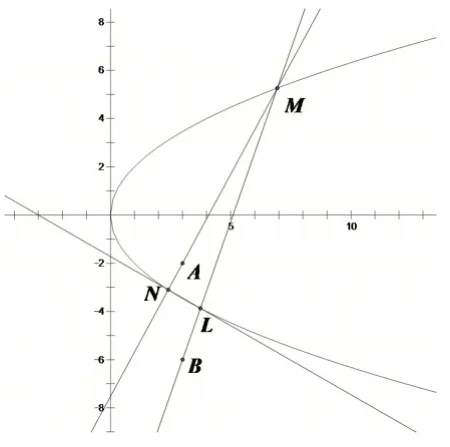
解法一：设M(x0,y0)，N(x1,y1)，L(x2,y2)，则，直线MN的斜率为，则直线MN:

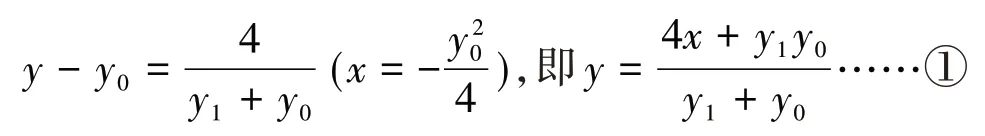
（注意：在计算过程中，我们还应敏锐地观察到如果通过两点坐标来表示直线方程的话，两直线MN和将A(3,-2)，B(3,-6) 分别代入①②两式得消去y0得y1y2=12，又则直线NL为。

解法二：①直线MN的斜率不存在时，A,B的横坐标相同，此时N,L重合，不符合题意，

②设M(x1,y1)，N(x2,y2)，L(x3,y3)，

直线MN:y+2=k(x-3)与y2=4x联立得k2-x2-(2k2+4k+4)x+(3k+2)2=0， ∴x1x2=

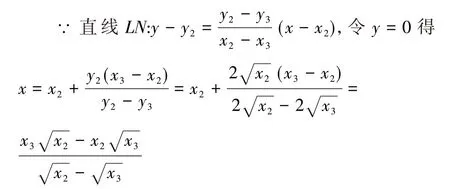
将代入上式消参得x=-3，因此直线NL恒过定点(-3,0)。

（一）分析例题脉络，归纳“设点法”适用题型特征

此题题设条件多，关系错综复杂，但是仔细分析可以发现，直线MN过A(3,-2)，ML过B(3,-6)，所以N,L两动点归根结底是随着动点M的变化而变化的，从而动直线NL其实跟动点M密切相关，所以此题可以采用“设点法”，将动点M的坐标设出，找出点N,L的坐标与M的坐标的关系，进一步表示动直线NL的方程，最后利用方程来分析定点问题。

实际上，通过总结近年来的一些高考试题及各地模考题，可以发现这样的规律：一般地，如果我们把一道解析几何解答题看成一个情节跌宕起伏的故事［2］，故事的起因是“曲线上的某个动点”，故事的发展经过是“该动点的运动引发了其他点、线、或者几何量的变化”，故事的结局就是题目的结论。如果题目符合这种“动点起因”的特征，另外，在经过和结局中较少涉及如弦长这类与韦达定理关系密切的几何量的计算时，通常可以采用“设点法”。

（二）比较两种解法，体会“设点法”的计算优势

解法一“设点法”解题过程中，用两点M,N坐标表示出直线MN方程，再利用点的坐标满足抛物线方程来化简直线方程。并且，解题中敏锐地观察到如果通过两个点的坐标来表示直线方程的话，两直线MN和ML方程的表示过程完全一样，直线方程的结构形式也一样。可直接同理得到，不必计算两次，这将大大减小计算量。

解法二“设线法”解题过程中，需要直接用到N,L两个点的坐标，与两个一元二次方程根与系数的关系没有明显的直接联系，若用求根公式将N,L两个点的坐标分别用两直线斜率k1,k2表示出来，再进一步表示直线NL方程，则计算量太大，不易进行实际操作。故在设MB方程时，将斜率用点M坐标表示，进而表示出直线MB方程，用设而不解的方法，结合韦达定理研究M,N,L三个动点坐标的关系从而研究动直线NL的方程，这样处理虽然可以进行操作，但是，计算量仍然太大，尤其在最后一步消参的过程中，对学生运算能力和运算技巧的要求太高，所以对此题而言“设线法”不是好的方法。

（三）思考解题过程，总结“设点法”解题模式

可以看到，在整个解题过程中，动点的坐标贯穿始终。题目几何条件的代数转化，结论的直线方程的表示，都依赖动点坐标。在用“设点法”解题的过程中，要始终具有目标意识，用敏锐的观察力，分析条件和目标的差异，用动点坐标作为参数去表示其他的点、线或几何量，并要充分利用动点坐标满足曲线方程的条件，及时进行有效地化简调整（常用平方及xi,yi的切换），将条件不断向目标转化，推进解题过程，这是“设点法”的大致解题模式。可以将这个模式总结为：设点——表示——化简转化——结论。

解析几何最大的难点在于：①不知从何做起（即设点与设线的选择；②计算繁琐“永无止尽”。要突破这两点就要胆大心细脚踏实地去细细品味例题，总结出自己的思路与思想［3］。下面表格对这两种方法进行了总结［3］：

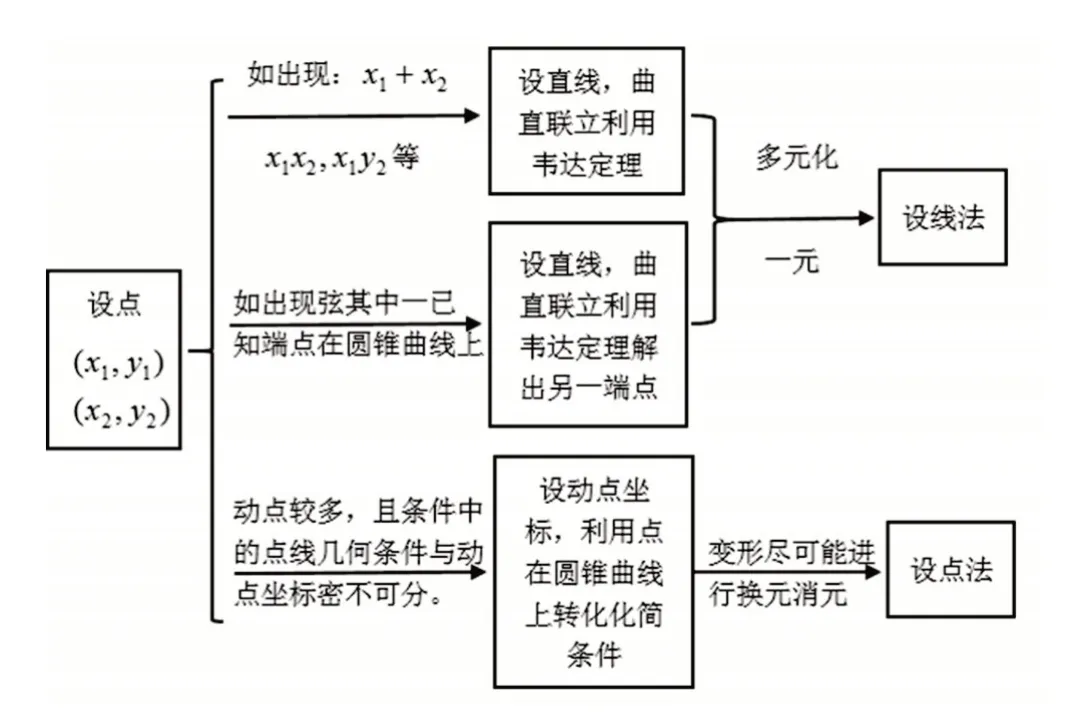
综上所述，高三解析几何的复习不仅需要培养学生知难而进的意志品质，更需要总结出一套行之有效的解题思路。在解题过程中要有目标意识，在用设点法或设线法求解时，要注意“主”与“辅”的关系［4］，要始终围绕目标和解题计划展开求解，抓住问题的主要矛盾，抓住矛盾的主要方面。在设点或设线法中，若能用某个点的坐标或某直线方程中的某一个或几个变量去表示其余的点的坐标或直线的方程，这样抓住“牛鼻子”就使得定值证明、最值求解和取值范围问题迎刃而解了。