矩形管接头疲劳失效位置预测及应力因子分析

谢素明，熊子斌，牛春亮，2

(1.大连交通大学 机车车辆工程学院，辽宁 大连 116028;2.大连海洋大学 机械与动力工程学院，辽宁大连116023)*

工程实践表明，焊接结构中疲劳失效主要发生在接头部位，因此，焊接接头的抗疲劳设计备受关注.经过数十年持续研究已经认识到焊接接头疲劳具有独有特征:焊接接头的疲劳失效模式是可以明确区分的，即它可能从何处开始出现裂纹，一旦出现裂纹，裂纹又可能朝着哪个方向发展;至少在寿命区间内，焊接接头的S-N曲线数据具有趋于一特有的斜率;平均应力对焊接接头的S-N数据没有显著影响［1］.

焊接结构疲劳评估方法可归纳为两大类:一类是凭借实验室里的S-N曲线数据计算疲劳寿命的传统的名义应力法［2］或热点应力法;另一类是以结构应力与断裂力学理论出发，基于两阶段裂纹扩展速率推导的主S-N曲线方程的结构应力法［3］.丁彦闯等［4］以焊接接头的累积损伤为约束，采用基于试验设计的近似模型优化策略，基于名义应力法对某焊接构架进行了抗疲劳轻量化设计;肖守讷等［5］基于多体动力学理论和有限元方法，对机车车体牵引座进行了基于名义应力法的疲劳寿命预测，并对仿真计算结果进行了验证;谢素明等［6］基于结构应力法和AAR标准中的载荷谱，预测了某重载运煤敞车车体焊缝的疲劳寿命，其薄弱部位与车体实际发生疲劳裂纹部位基本吻合.

当前轨道交通装备制造行业的复杂焊接结构产品设计已经开始执行EN15085标准《轨道车辆及零部件的焊接》，其中 EN15085-3［7］或 GB/T25345-3［8］是关于焊接结构(接头)的设计规范，在设计阶段不仅要对接头进行疲劳强度评估，还要计算其应力因子，进而明确接头应力类别，并结合接头安全类别，最终确定焊缝性能等级及焊缝检查等级.本文借助矩形管接头分析BS7608 2014+A1:2015标准中名义应力法和ASME标准中结构应力法涉及的接头名义应力和结构应力分布特点;并分别利用这两种方法对该管接头进行疲劳失效位置预测同时借助相关试验验证;同时结合BS EN15085-3标准分析接头焊缝应力因子以及确定应力等级.

1 焊接接头上的应力分布

外载荷作用下，沿板厚方向接头处的应力σ可分解为膜应力σm，弯曲应力σb及非线性峰值应力σnl，如图1所示.

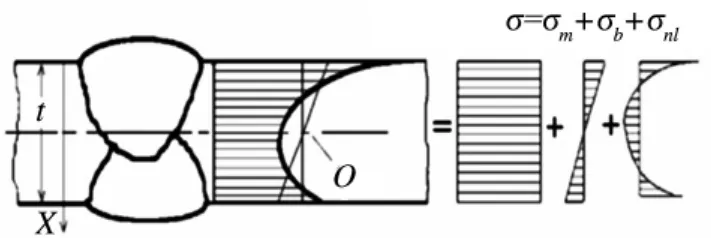
图1 接头上应力的非线性分布

图1 所示接头上的这些应力分量中，膜应力σm等于沿板厚t计算出来的平均应力:

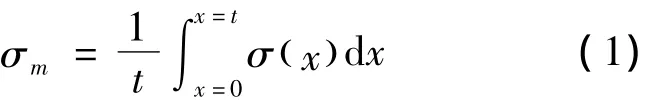
式中，x=0为板的上表面，x=t为板的下表面.

弯曲应力σb沿一条通过点O(0点为膜应力与板中性面的相交点)的直线分布，即沿板厚线性分布.弯曲应力分布直线的斜率应能保证非线性峰值应力σnl沿板厚非线性分布分量自平衡，这两个应力分量的计算公式为

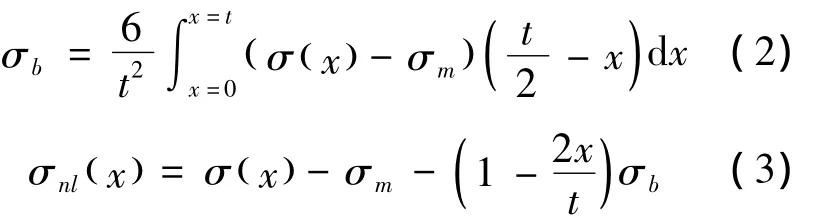
从图1可以看出接头焊趾处的应力σ是高度非线性的，应力分量σnl是自平衡的，与外载荷没有关系，也就是说只有其它两个应力分量σm，σb与外载荷直接关联.

基于名义应力法的BS7608标准提供分级S-N曲线数据时，其施加的疲劳载荷方向是给定的，因此，其数据中包含的名义应力方向或与焊缝平行或与焊缝垂直.对于简单焊接接头利用上述公式很容易计算接头应力，然而面对实际复杂工程问题时，经常会遇到复杂焊接接头承受复杂外载荷导致的接头焊趾处主应力方向与焊缝方向不平行，也不垂直的现象，为解决这个问题，BS7608标准提出如果可以事先判断出潜在的疲劳裂纹方向，那么在垂直该方向的±45°角度范围内拾取用有限元法计算的最大主应力作为名义应力.然而，这样拾取的应力是表面应力，它不能代表焊趾(或焊根)所在截面沿厚度的应力分布，同时当采用有限元方法计算应力时必然会面临依赖单元尺寸的问题.

断裂力学理论指出:控制焊缝裂纹扩展速度的应力不应仅仅是焊趾处表面应力，而是从焊趾开始垂直于板截面上的全部应力的分布状态.可以看出:应用名义应力法评估复杂焊接接头疲劳问题时必会受到相当大的限制.ASME标准中的结构应力是基于自由体切面法，采用有限元分析输出节点力和弯矩，且在满足平衡条件下用结构力学的方法获得的.

假设一个焊接接头的远场外力在截面上既有拉伸贡献的膜应力也有弯曲贡献的拉应力，与外力平衡的是膜应力与弯曲应力之和.板厚给定，截面内均匀分布的膜应力

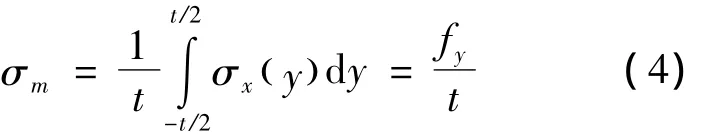
而截面内产生的弯曲应力

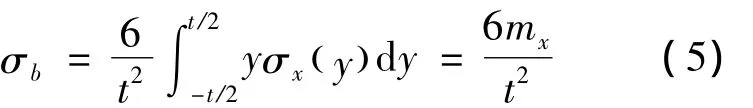
结构应力定义为与外载荷平衡的膜应力与弯曲应力之和

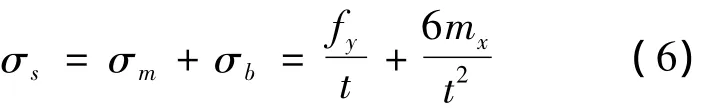
由式(6)可以看出，在计算结构应力时首先要计算线力和线矩，而线力与线矩是指焊线处单位长度上的力与力矩.在有限元计算时，单元边上的分布载荷要向节点转化，而结构应力在利用节点力求线力和线矩时，却是这个过程的逆过程，还要将有限元求得的节点力和力矩转化为线力和线矩.

2 矩形管接头疲劳失效位置分析

如图2所示，经不同尺寸的两个矩形管焊接形成的管接头焊缝结构比较复杂.两个矩形管的截面外形尺寸分别为101.6 mm ×101.6 mm(管1)和50.8mm×152.4 mm(管2)，管壁厚和焊脚尺寸均为7.9mm.管材为A13R-RC7，其屈服强度为345MPa.

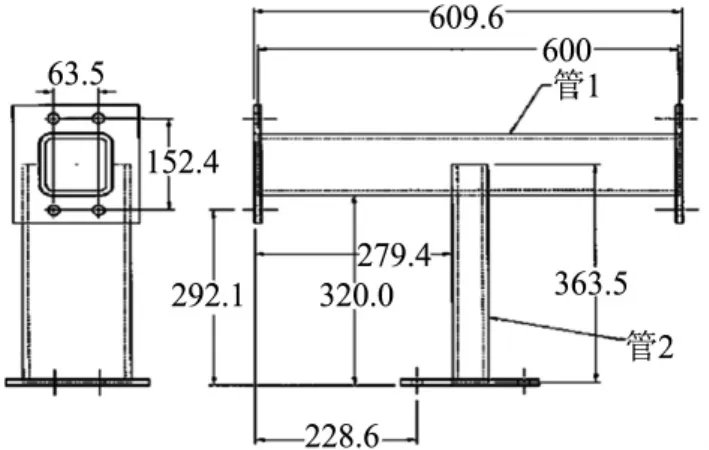
图2 矩形管接头几何

在管1截面中心上方317.5 mm处的刚性板末端施加17.8 kN的载荷，并且载荷循环特性R= -1.

根据矩形管的几何数据，建立含有焊缝细节的管接头有限元分析模型，采用CERIG单元固定管1中心，BEAM单元模拟刚性板，在317.5 mm高度施加载荷，在管1另一端和管2施加全约束，如图3所示.

图3 矩形管接头的分析模型

在外载荷作用下，位于管1上的焊线a和管2上的焊线b的最大主应力、Von.Mises应力、结构应力沿焊缝长度方向上的变化曲线如图4所示.从图4可以看出:焊线a和焊线b上，除终点区域外最大主应力和Von.Mises应力的变化规律相似，且最大主应力的值略大于Von.Mises应力的值;终点区域的Von.Mises应力值要大于最大主应力的值.结构应力的变化规律与它们不同，

图4 矩形管接头上的各应力分布曲线

在焊线两端的值较小.Von.Mises应力和最大主应力均在焊线 a的始点达到最大值，分别为156.41 MPa和180.25 MPa(参见图5);焊线b上的最大主应力和Von.Mises的最大值远小于发生在焊线 b拐角处的结构应力，最大值为182.29MPa，该拐角位置正是文献［9］中管接头的失效位置.

图5 矩形管接头上最大主应力云图

3 接头应力的影响因素分析

为考察模型单元尺寸对管接头焊缝处各类应力的影响程度，建立四种不同有限元模型，如图6所示.在外载荷作用下，三种壳模型焊缝端部和拐角部位的最大主应力、Von.Mises应力、结构应力的对比结果如图7所示.从图中可以看出:在焊缝端部和拐角处，最大主应力和Von.Mises应力的数值随单元尺寸的增大而减小;在拐角处，1/2t模型和1t模型的结构应力值基本一样，且比2t模型的结构应力值小.究其原因:2t模型的单元大小16 mm无法模拟拐角处的几何结构(圆角半径12 mm)，因此改变了拐角处的传力关系.

图6 四种不同管接头有限元模型

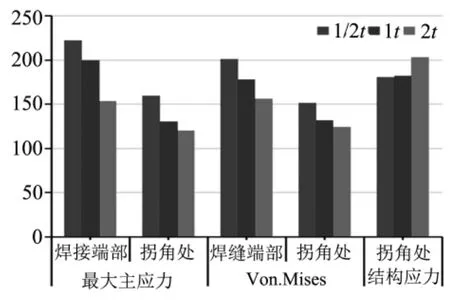
图7 单元尺寸对焊缝各类应力影响的对比

为进一步研究单元类型对结构应力的影响，建立实体单元的有限元模型(见图6)，模型中板厚度方向至少应有两层以上的单元，且焊线沿板厚方向的节点要共线.图8给出了1t壳模型与实体模型的焊线a和b上的结构应力变化曲线.

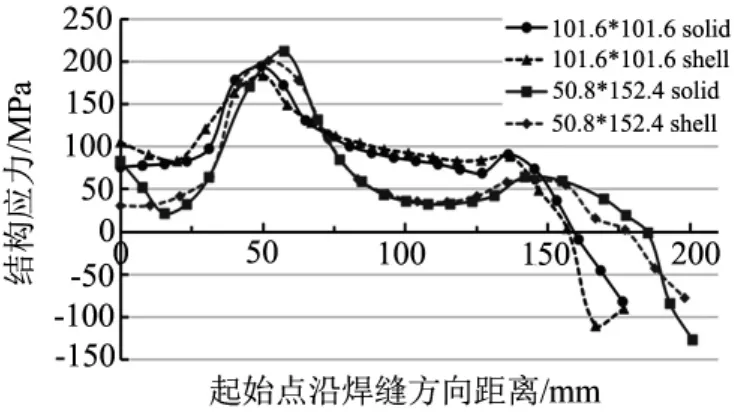
图8 壳模型与实体模型的结构应力对比

从图8可以看出:实体模型得到的结构应力与可以模拟出焊缝轮廓的1t壳单元模型的应力分布规律和数值基本一致.这一结果源于焊缝上结构应力的计算基础是焊趾截面上的焊线节点力的合力与接头外力相平衡.

4 矩形管接头应力因子分析

当矩形管接头承受 ±17.8kN的疲劳载荷的设计寿命为12万次时，分别使用名义应力法和结构应力法计算管接头焊线b的应力因子.

BS7608标准中将钢结构接头细节分成13个级别，焊接接头的应力变化范围Sr与疲劳寿命N之间的关系为

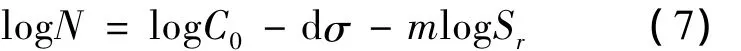
式中，C0是基本S-N曲线数据中的常数;d是低于均值的标准偏差的数量;σ是N的对数下的标准偏差;m是双对数坐标系下的反向斜率.依据焊线b区域的主应力方向(参见图9)与管接头细部结构，在BS7608标准中很难找到一一对应的接头，因此，选择F级和F2级的疲劳等级的疲劳性能参数:C0=1.726×1012，1.231×1012;σ =0.218 3，0.227 9;d=0;m=3.然后，由式(7)可计算出设计寿命下，接头的F级和F2级的许用疲劳强度值分别为Δσref=243MPa，Δσref=217 MPa.将焊线b的计算主应力变化范围除以许用疲劳强度值，就可以获得焊线的应力因子，如图10所示.

图9 接头焊线b附近的主应力矢量图

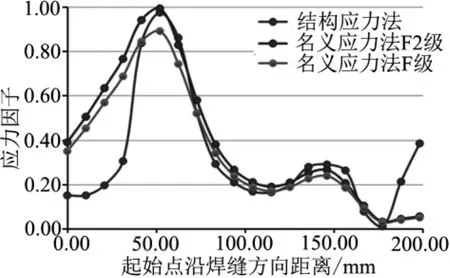
图10 接头焊线b的应力因子

基于ASME标准中结构应力的主S-N曲线方程

式中，ΔSs为等效结构应力变化范围，Cd及h为试验常数.利用结构应力法计算管接头焊线b的应力因子时，选择中值的主S-N曲线参数:Cd=19 930.2，h=0.319 5.由式(8)可计算设计寿命下接头的ΔSs为475 MPa.考虑板厚t、载荷弯曲比r的无量纲函数I(r)对疲劳评估的综合影响，结构应力与等效结构应力的关系为

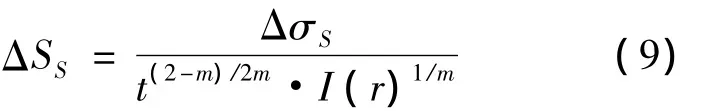
式中，m为裂纹扩展指数，约为常数3.6.

利用焊线b的计算结构应力变化范围和式(9)，可得焊线b的等效结构应力变化范围;然后，除以设计寿命下的ΔSs就可获得焊线的应力因子，如图10所示.

从图10可以看出:焊线b除两端区域外，应力梯度变化小时，名义应力法与结构应力法计算的应力因子的变化趋势一致，均在焊缝拐角处达到最大值.名义应力法选择F级应力因子最大值为0.89，应力等级为中.由于选取原则更保守选择，F2级应力因子比F级更大，最大值为0.99，应力等级为高;结构应力法焊线b的应力因子最大值为0.98，应力等级为高.

5 结论

(1)矩形管接头焊缝的结构应力与最大主应力和Von.Mises应力的分布规律不同，在焊缝拐角区域结构应力的数值远大于其它两类应力的数值，尤其在疲劳试验的失效部位处结构应力的数值最大为182.29MPa，比该处的最大主应力高出73.92 MPa;

(2)当矩形管接头分析模型的单元尺寸不同时，焊缝的最大主应力和Von.Mises应力的变化显著;可以模拟焊缝拐角处几何结构特征的1/2t模型和1t模型的结构应力值基本相同;

(3)相同外载荷和分析模型时，基于结构应力法的矩形管接头焊缝应力因子比基于名义应力法F级的大，略小于F2级的，应力因子最大值为0.98，应力等级为高;

(4)考虑到位于应力梯度变化大区域内的接头焊缝的名义应力受分析模型单元尺寸的影响大的事实，以及复杂接头难以在BS7608中找到近似的接头类型，建议复杂接头疲劳评估时，应采用结构应力法.