一类考虑潜伏期和隔离机制的传染病模型的动力学分析

郭树敏

（韶关学院 数学与统计学院，广东 韶关 512005）

近年来不断有新型传染病出现，例如重症急性呼吸综合征、埃博拉病毒病、人感染高致病性禽流感、朊毒体病、中东呼吸综合征等［1-2］.一旦有新的疫情发生，就有学者根据新型传染病传播的机理建立模型并进行理论分析［3-4］.有很多呼吸类传染病病毒的潜伏期较长，防控手段主要就是隔离，因此，本文建立了考虑潜伏期和隔离机制的传染病模型.

1 模型的建立

本文的建立的模型为：

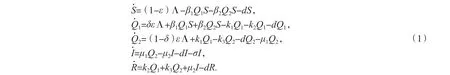
其中，S 是易感者，Q1是未被隔离的潜伏者，Q2是被隔离的潜伏者，I 是已发病的染病者，R 是康复者.Λ是外地迁入的以及本地新生的人口数，ε 是感染病毒者在新增人口所占比例，β1是未被隔离的潜伏者与易感者接触的感染率，β2是被隔离的潜伏者与易感者接触的感染率，d 是自然死亡率，δ 是未被隔离的潜伏者在新增感染者中所占的比例，k1是未被隔离的潜伏者被发现并隔离的比例，k2是未被隔离的潜伏者自愈的比例，k3是被隔离的潜伏者自愈的比例，μ1是被隔离的潜伏者发病的比例，μ2是发病的染病者中被治愈的比例，σ 是因病死亡率.建立模型时做了如下假设：

（1）新增人口中有部分是已感染病毒的潜伏者，其中部分被发现继而被隔离，还有一部分未被发现从而未被隔离；

（2）感染病毒的潜伏者中有部分免疫力较强，没有明显的严重症状，不需要治疗就会自愈；

（3）易感者接触潜伏者会有一定几率感染，已发病的感染者通常都会就医，接触易感者并传播病毒的可能性很小，故不考虑其传染性.

2 模型分析

假设当t ≥ 0 时，系统（1）中的变量和参数始终为正.由系统（1）的生物学意义得：

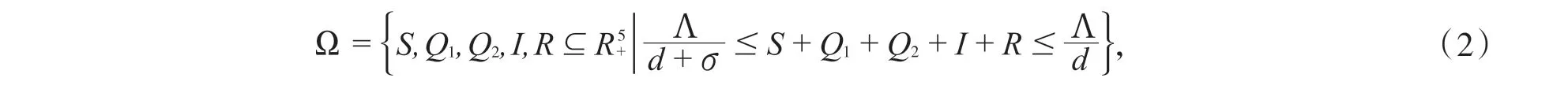
其中Ω 为系统（1）的正向不变集.容易看出系统（1）的前3 个方程与变量I，R 无关，其稳定性可由以下系统分析：

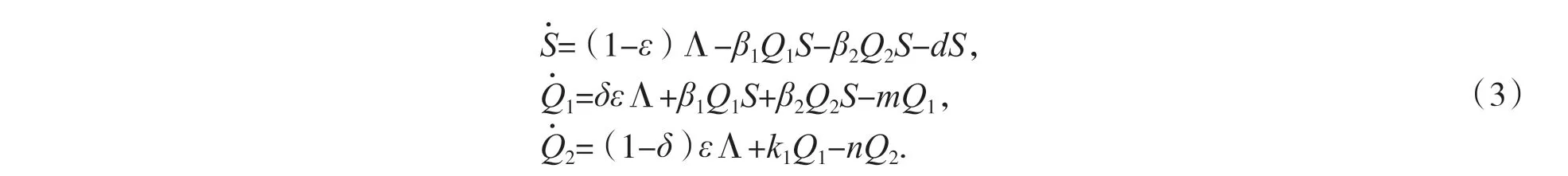
系统（3）满足初始条件为：S（0）＞0，Q1（0）＞0，Q2（0）＞0，其中m=k1+k2+d，n=k3+μ1+d.系统（3）有正平衡点E*（S*，Q1*，Q2*），由方程a1Q1*2+a2Q1*+a3=0确定，其中a1=m（β1n+β2k1）＞0，a2=mβ2（1-δ）εΛ+mnd-Λ（δε+1-ε）（β1n+β2k1），a3=-β2（1-δ）εΛ＜0.因此方程始终有唯一的正根，系统（3）有唯一的正平衡点E*.下面讨论当ε=0，即无输入感染者时，系统（3）的基本再生数.

此时系统有无病平衡点E0（Λ/d，0，0）.设x=（Q1，Q2，S）T，系统（3）可以写为：

F（x）和V（x）在无病平衡点E0的Jacobian 矩阵为：

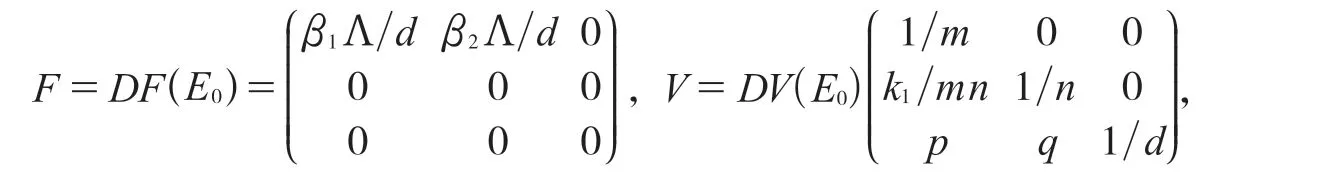
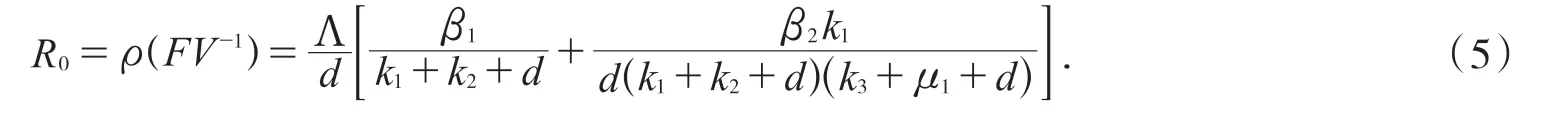
3 平衡点的稳定性

下面讨论正平衡点E*（S*，Q1*，Q2*）的全局渐近稳定性.系统（3）的Jacobian 矩阵为：

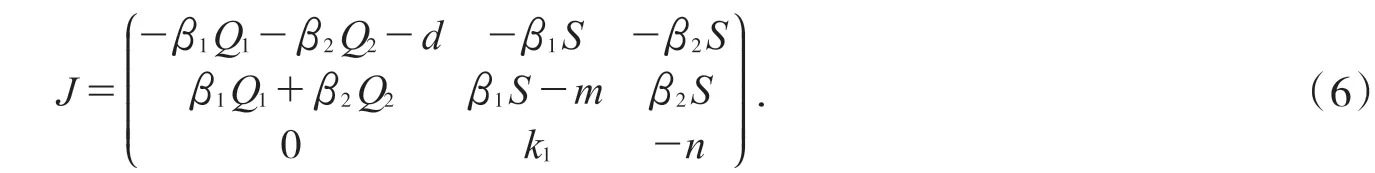
于是可得J 的第二加性复合矩阵为［2］：

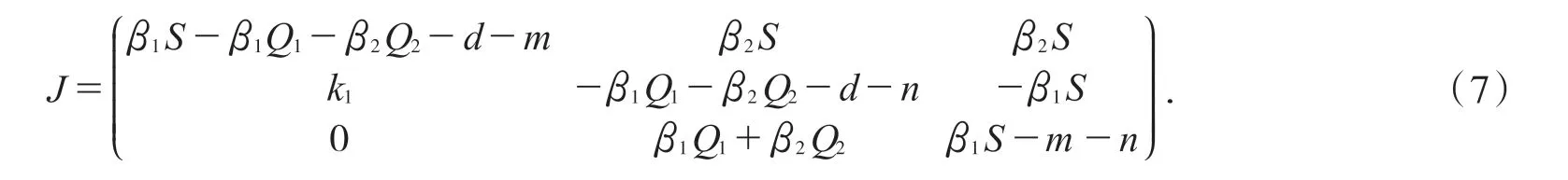
令：

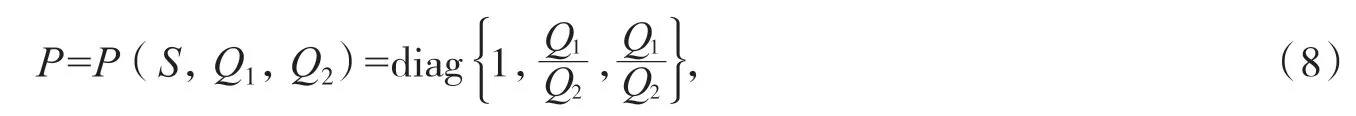
则：

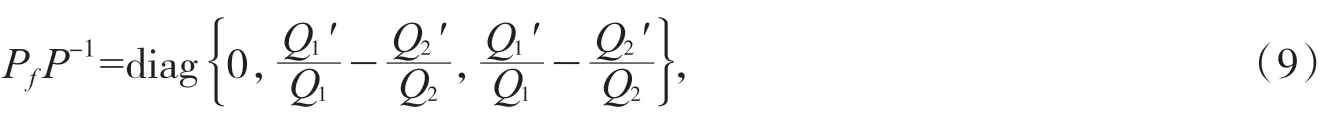
从而：

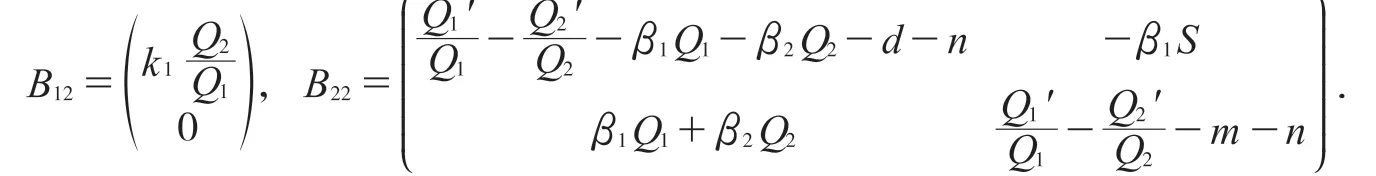
设│·│是R3中的范数，定义为│ω1，ω2，ω3│=max{│ω1│，│ω2+ω3│}，其中（ω1，ω2，ω3）表示R3中的 向 量，L 表 示 范 数 的Lozinskii˘测 度，L（B）≤ sup{g1，g2}=sup{L1（B11）+│B12│，L1（B22）+│B21│}. 其 中│B12│，│B21│是对应于向量范数l1的矩阵范数，L1是对应于范数l1的Lozinskii˘测度，因此：

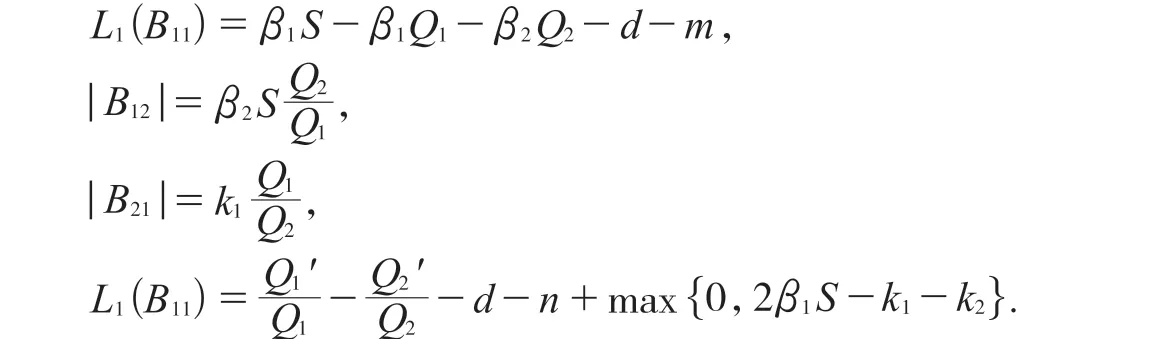
于是：

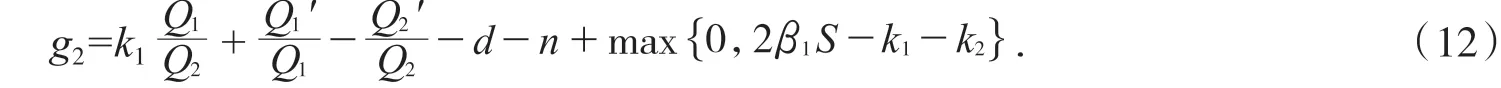
由系统（3）的第二式可得：

把（13）和（2）代入（11）式，可化为：

由系统（3）的第三式可得：

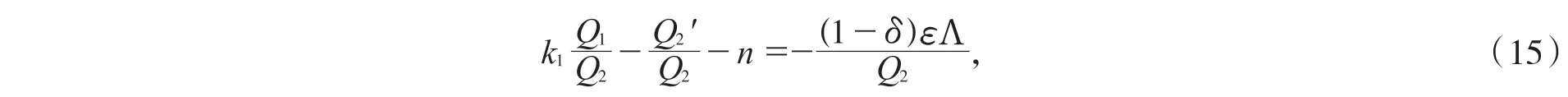
把（15）和（2）代入（12）式，可化为：

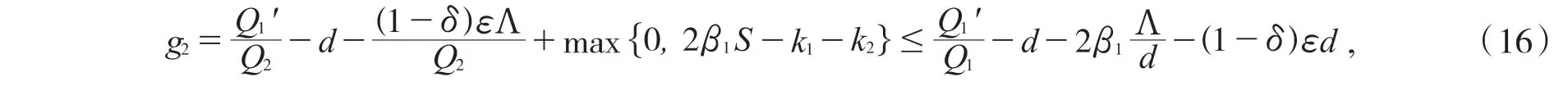
则：

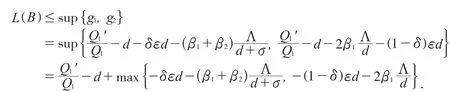
情况1：如果δ＜1-δ，即时，有那么：

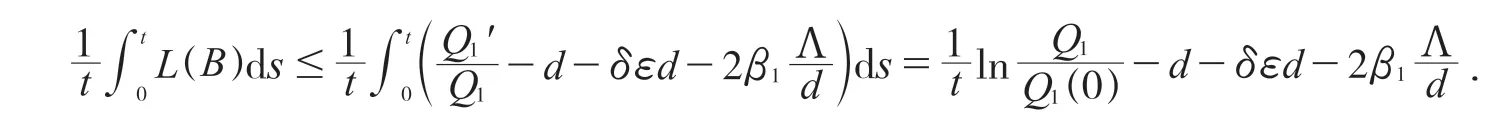
则：

情况2：如果δ＞1-δ，即时，有那么：

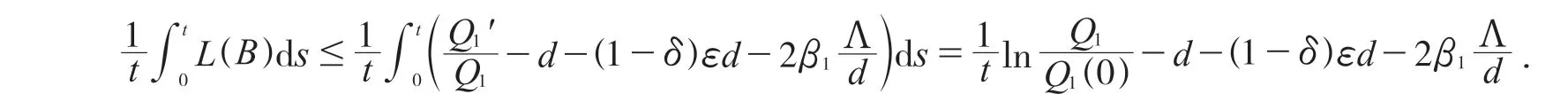
则：

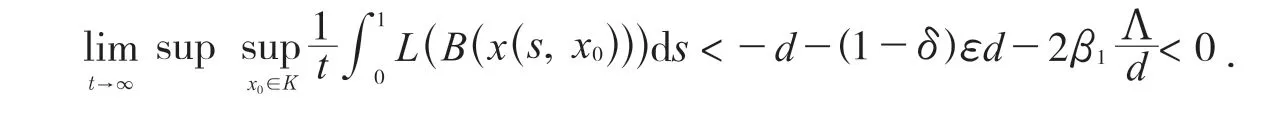
如上面所说，由文献［6］中Muldowney 给出的准则有如下定理.

定理当R1＞1 时，正平衡点E*（S*，Q1*，Q2*）全局渐近稳定，其中：当时，当时，

4 结语

本文建立了一类考虑潜伏期和隔离机制的传染病模型，通过分析其参数可知，无输入感染者时，减少潜伏期感染者与易感者的接触几率能有效控制疾病传播，特别是减少未隔离的潜伏期染病者与易感者的接触能更加有效降低疾病传染效率.当输入的未隔离潜伏者不过半时，减少未隔离的潜伏者的数量可以有效控制疾病传播；当输入的未隔离潜伏者过半时，减少未隔离潜伏者的数量已无效果.因此封闭疫情严重地区，全员居家隔离，减少人员流动，并对外来者普及疫病筛查，染病者及时进行隔离，是控制此类传染病传播最有效的手段.