基于多模式样本t 检验的精准化学习模型构建与研究

郭 丽

（安徽电子信息职业技术学院 软件学院，安徽 蚌埠 233000）

高职院校学生学习水平亟待通过各种内外因素共同促进，提高学生的学习能力.制约学生学习绩效的多种因素将直接影响到他们未来能否成才.传统的教育教学方法按部就班，无法真正从根本上促进和提高学生的学习积极性，务必从根源上匹配出适用于高职院校学生的教学方法等.通过大数据技术，开拓高职院校学生绩效因素比较研究的新领域.依托高职院校学生学习习惯等建立数据分析模型可以更好地分析制约学生学习绩效研究的多种因素.

从大数据视域对教学改革进行解读，充分利用大数据技术，提高教学改革的针对性和适应性，辅助人才培养工作的稳步推进.通过大数据技术智能收集、处理数据，提供精准的反馈信息，实现了教学的实时跟踪，精准诊断，对学生学习过程的评价更客观、真实、准确.随着数据流在教学各个环节的生成与运行，大数据智能处理驱动的精准教学逐步替代传统教学模式，见图1.

基于学生学习情况信息采集的数据背景下，通过多模式样本t 检验方法进行模型的分析与构建实验，样本实验成熟后提高至高数量级大数据样本，保证结果的更加精准性.目前，在实验阶段首先抽取学院小样本数据做出基础实验.独立样本t 检验是在比较平均值的不同情况后，通过对每个隶属于总体样本的独立样本进行分析，进一步推断两个样本之间的方差齐性情况，即显著性差异情况.成对样本t 检验的数据是同一群被试或个案被测两次而获得的，即同一群体有前测和后测两组测试数据.其研究目的也是均值的差异情况，它与单样本t 检验又有不同，成对样本t 检验是进一步推断隶属总体之间的差异情况，即总体间是否存在显著性差异.

图1 大数据智能驱动精准教学模式框架图

1 选取试题库使用被试进行独立样本t 检验

1.1 确定独立样本t 检验的前提条件

被抽取的样本源符合钟形分布，即正态分布形态；两样本之间无交互效应，独立存在；样本变量不可为离散型变量，符合连续型数据特征［1］.选择样本时，从一个总体中抽取一组样本与从另一个总体抽取的一组样本彼此独立，没有任何影响，它们分别属于不同的总体，样本数量可以相等亦或不相等.与单样本t检验一样，在写备择假设时这里的显著差异写法包括显著不等于（H1：µ1≠µ2）、显著小于（H1：µ1＜µ2）和显著大于（H1：µ1＞µ2），案例基于检验显著不等于的情况，即只做双侧检验，如果做单侧检验，需要通过双侧检验数据后再进行人为判断［2］.

1.2 独立样本t 检验步骤

利用随机试题库筛选出被试共50 人，作为前测；然后将他们随机分组，1 组采用传统教学方法教学，2组采用大数据精准化方法教学；干预完成后用随机试题库进行第二次测量，这是后测.传统教学方法和大数据精准化教学方法哪种方法对于教学质量提高更有效可以基于独立样本t 检验模式，通过莱文方差同性检验和平均值同性t 检验结合做出诊断，确立样本是否随机分组［3］.假如被试者随机分组成功，即随机分配的两组学生在不同教学方法干预前的水平不存在显著性差异，两组样本数据又是相互独立的，符合独立样本t 检验的前提条件.但在数据精准性方面，要先测试前期分组数据是否随机，才能确保后续数据分析的正确性.

1.2.1 独立样本t 检验的原理与步骤

步骤1：建立原假设H0与单样本t 检验一样，独立样本t 检验的数值也存在3 种不同情况：显著不等于、显著大于和显著小于.

步骤2：确定检验统计.样本总体均符合钟形正态分布曲线，方差σ12和σ2确定数值后，对两样本进行抽样分布估计，即σ212，可以表示为：

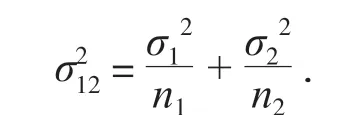
表达式中，σ12为第一个样本的总体方差，为第二个样本的总体方差，n1和n2代表样本数据中的数量.由于之前已确定样本符合正态分布，可以采用Z 检验得出的莱文统计量做出差异性判定.因为方差的情况不同需要采用不同的t 检验方式，所以在进行两独立样本t 检验之前，首先应当明确两者的方差是否相等，以此判断应该采用哪种检验统计量［4］.

步骤3：观察莱文统计量F 值以及检测性双尾P 值.根据t 统计量所服从的分布计算对应的概率P值，与单样本t 检验不同的是，独立样本t 检验的分析结果会给出两个t 统计量供选择，需要根据相应的检验结果选择合适的统计量.

步骤4：设定显著性水平α 与概率P 值进行比较，做出统计决策.

1.2.2 两独立样本t 检验的决策分两步进行

（1）考察两个独立样本的方差齐性问题. F 检验中的莱文统计量表判定方差是否相等，通过概率值P查看两样本之间是否存在显著性差异［5］.若莱文统计量检验中，检测性双尾P＞0.05，两总体方差齐性；若概率P＜0.05，则判定两总体方差不相等.

（2）判断两独立样本的总体均值是否有差异.第一步证明的方差相等与否为选择合适的t 检验提供了依据，再通过t 检验的模式，判定两样本是否存在显著性差异，莱文检验中，将P 与数值0.05 进行差异性比较，得出结论.检测性双尾P＞0.05，不存在显著性差异；检测性双尾P＜0.05，存在显著性差异，见表1.

表1 组统计量

表2 独立样本检验结果

首先，检验两组被试的前测差异性.从表2 可以看出两者的方差是没有差异的（F=0.299，P=0.587），进而对两者进行独立样本t 检验，发现两者均值差异也是不显著的（t=0.955，自由度df=48，P=0.344），可确定随机分组是成功的.

其次，检验两组被试后测的差异性.表2 中F=1.569，P=0.216，由于P ＞0.05，即两者的方差是没有差异的，进而对两者进行独立样本t 检验，发现两者均值差异也是不显著的（t=-2.624，自由度df=48，P=0.012），且P ＜0.05，可确定传统教学方法和大数据精准化教学方法的干预效果是有显著性差异的［6］.从表1 可以看出传统教学方法干预后测试平均分是50.480 0，大数据精准化教学方法干预后测试平均分是56.360 0，则大数据精准化教学方法干预后的测试得分显著高于传统教学方法，即大数据精准化教学方法教学效果更好.

2 两配对样本t 检验的原理和步骤

在进行独立样本t 检验之前，提出条件假设，查看样本形态分布是否符合钟形正态分布特征［7］.再则两样本均为独立个体，两样本间无交互效应，因而各自样本数量勿需一致，另外需要保证样本变量符合连续型变量的要求［8］.在数据分析与构建模型过程中，首先要判断使用前提条件是否符合，决定使用的检验方法.两配对样本t 检验的原理和步骤如下：

步骤1：建立原假设H0，存在3 种不同情况：显著不等于、显著大于和显著小于.

步骤2：由于总方差不确定，抽取样本的方差可以作为总体样本方差的替代，其F 检验值为：

只要样本足够大（n ≥30），都可以用近似正态Z'检验［9］，其统计量为：

步骤3：得到F 值和检测性双尾P 值［10］.

步骤4：设定显著性水平α 并与概率P 值进行比较，做出统计决策.

当P＞α 时，不存在显著性差异； 当P＜α 时，存在显著性差异.

收集某专业数据只涉及一个群体35 个个案，每个个案都有4 门课程的学习时长数据，可理解成被测试了4 次，现在要比较4 门课程学习时长对于学习效果的影响是否存在差异，可以采用成对样本t 检验进行分析，对两门课程的学习时长进一步做两两比较.

表3 可以看出6 个配对组各自的统计指标，表4 指出了6 个配对组的差异性检验：“课程1-课程2 =-7.326 540 00”，说明课程2 的学习时长比课程1 的学习时长从均值上来说增加了7.326 540 00，对其进行检验的统计量t 值为-3.451，自由度df 为34，概率P 值（显著性）为0.002＜0.05，说明课程2 的学习时长要显著大于课程1 的学习时长；同理，课程2 的学习时长也显著大于课程3 和课程4，其他配对组的差异都不显著.通过样本的差异性分析，对于后期人才培养方案的修改提供了强有力的理论及数据依据，为后续的课程体系建设提供支持与保障.

表3 成对样本统计量

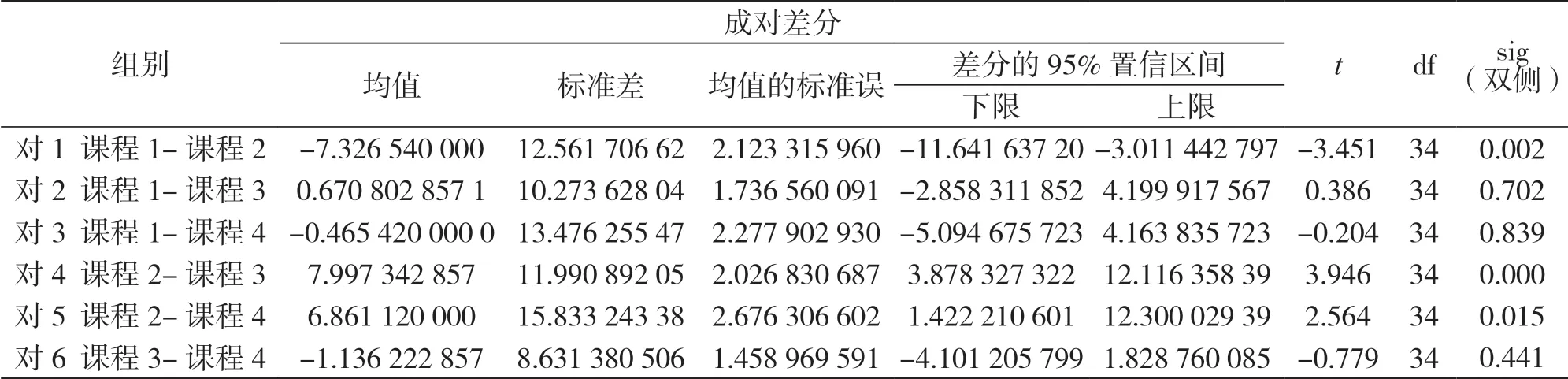
表4 成对样本检验

3 结语

面对迅速崛起、异军突起的高等职业教育，在大数据背景下，对制约高职院校学生学习绩效的各因素进行对比研究，发现各因素中的主要矛盾及次要矛盾，确立研究的重点及次重点，同时高校学生的学习习惯、学习动机等亦是本课题的研究基础.通过大数据样本分析为多重因素的研究提供强有力的数据保障与技术支持，努力为学生营造高绩效良好的学院教育生态环境.