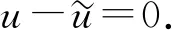一类四阶低曲率方程弱解的存在唯一性

靳曼莉, 郭 丽

(北华大学 数学与统计学院, 吉林 吉林 132013)

0 引 言

四阶抛物型偏微分方程在材料科学、 工程学、 生物数学、 图像处理等领域应用广泛. 由于四阶线性扩散中的高频振荡通常比二阶扩散中的震荡衰减速度快, 且四阶方程还可以考虑曲率的作用, 因此在图像处理方面, 四阶偏微分方程比二阶方程的模拟效果更优.

Cahn-Hilliard方程[1]

通常被用来描述相分离过程中守恒浓度场的演化. You等[2]利用四阶方程

ut+2[g(2u)2u]=0

代替文献[3]中的二阶Perona-Malik型方程, 数值模拟结果表明, 该方程能更好地去除图像噪声, 保留边界, 使处理后的图像更自然. Lysaker等[4]在处理医学核磁共振图像时提出了如下四阶抛物型方程:

为提高图像的边缘检测并消除噪声, Wei[5]将边界提升控制泛函和超扩散算子引入Perona-Malik方程中, 得到了如下模型：

ut=div(d1(u,|u|)u)+div(d2(u,|u|,Δu)Δu)+e(u,|u|).

Bertozzi等[6]考虑四阶扩散方程ut+Δ(arctan Δu)=λ(f-u)的Neumann问题, 给出了该方程经典解存在唯一性的充分条件. Wang等[7]讨论了二维低曲率方程ut+Δ(arctan Δu)=0弱解的存在唯一性.

本文考虑如下四阶抛物型方程的初边值问题:

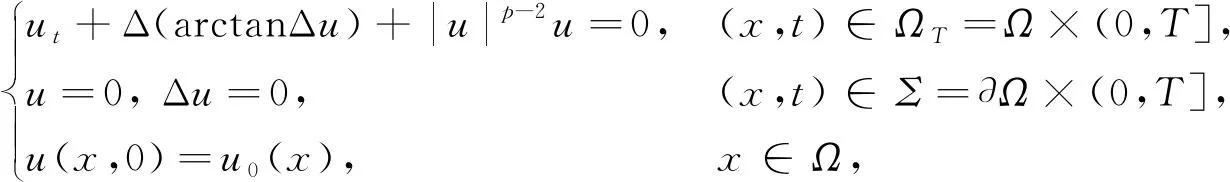
(1)

其中:Ω⊂2是具有光滑边界∂Ω的有界开区域;T是一个正数;p>2. 利用差分和变分的方法, 首先将发展型方程(1)利用差分的形式化为椭圆方程, 证明该椭圆问题解的存在唯一性, 然后证明差分后所得椭圆问题解序列的极限即为原问题的解, 最后应用文献[8-9]的正则性、 差分和变分法给出问题(1)弱解的存在唯一性证明.

1 主要结果

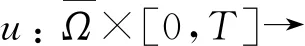
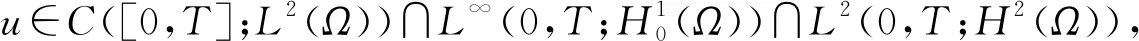
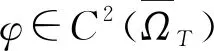
成立, 则称函数u(x,t)为问题(1)的弱解.

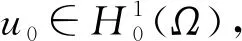
2 解的存在唯一性

令n为正整数,ε是一个小的正数,h=T/n. 首先考虑如下椭圆问题弱解的存在唯一性:

(3)

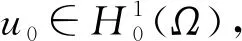
首先证明J(v)在V中有极小元u1(x). 因为0∈V, 所以

(4)

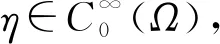
又因为

则

于是

对于函数fε(t)=εt+arctant, 有

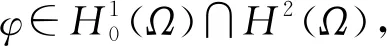
故

选取φ=u1-v1, 有

由于arctant为上的递增函数, 则式(5)等号左端的各项均非负, 因此u1=v1在Ω上几乎处处成立, 从而证明了问题(3)弱解的存在唯一性.

考虑如下抛物型方程的初边值问题:

(6)

其中ε是固定正数.

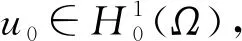
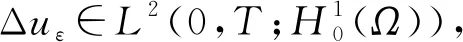
(7)

(9)

取φ=Δuk, 则有

于是有

对于h=T/n, 定义如下函数:

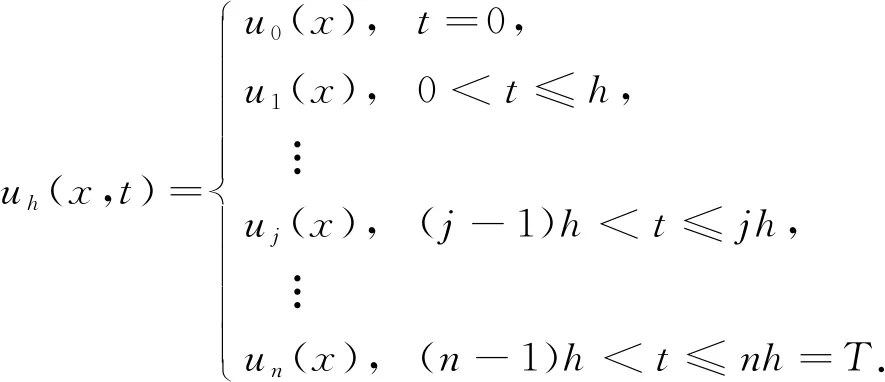
(11)

结合式(10)知, 对任意的t∈[0,T], 有

‖uh(x,t)≤‖u0,

故

‖uh(x,t)‖L∞(0,T;L2(Ω))≤‖u0.

(12)

将式(10)中的n个不等式相加, 可得

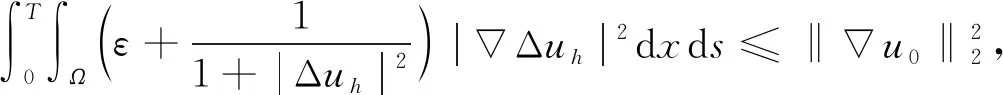
(13)

(14)

从而

于是

结合式(13)有

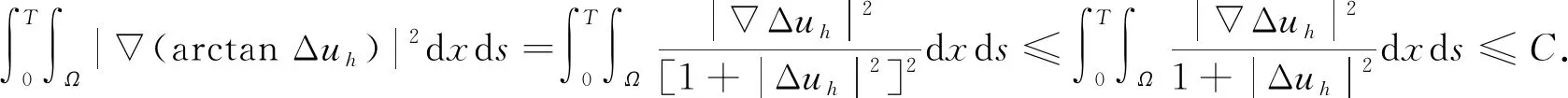
(15)

根据式(12)～(15)及Δuh|∂Ω=0, 可得

因此可抽取子序列(仍用uh表示), 使得下列结论成立：

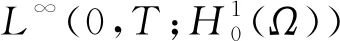
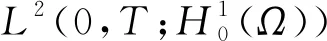
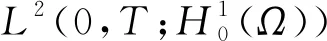
于是

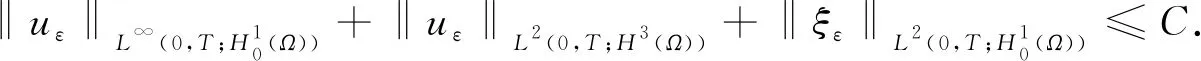
(16)

将式(17)对k=1,2,…,n求和, 由uh(x,t)的定义及条件φ(·,T)=φ(·,nh)=0可得

令h→0, 结合上述结论1)～3)及式(16)得

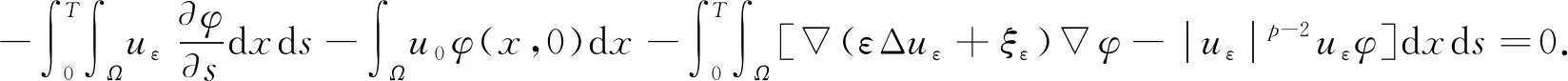
(18)

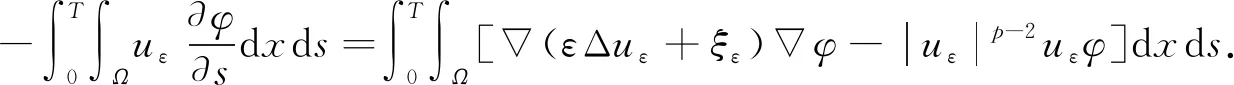
(19)

因为uε满足式(18), 所以为了证明uε为式(6)的弱解, 只需证明在ΩT上几乎处处有ξε=arctan Δuε. 取uε为式(18)的检验函数可得

(20)

取uk作为式(9)的检验函数可得

(21)

将式(21)对k=1,2,…,n求和, 可得

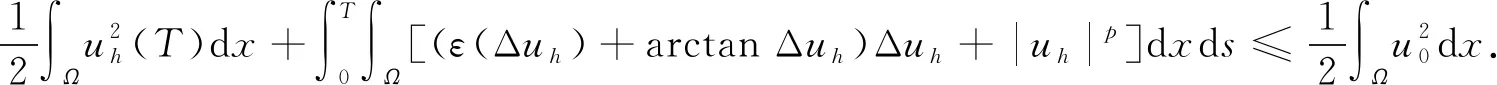
(22)

由于对任意的ξ,η∈, 有

(arctanξ-arctanη)(ξ-η)≥0,

因此对任意的v∈L2(0,T;H2(Ω)), 有

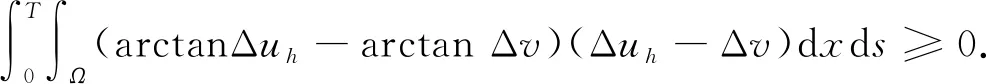
(23)

于是由式(22)可得

令h→0, 则有

由式(20),(24)知, 对任意的v∈L2(0,T;H2(Ω)), 有

即

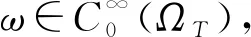
故在ΩT上几乎处处有ξε=arctan Δuε, 从而uε即为问题(6)的弱解, 因此完成了弱解存在性的证明, 且由式(22)可得式(7), 由式(10)可得式(8).

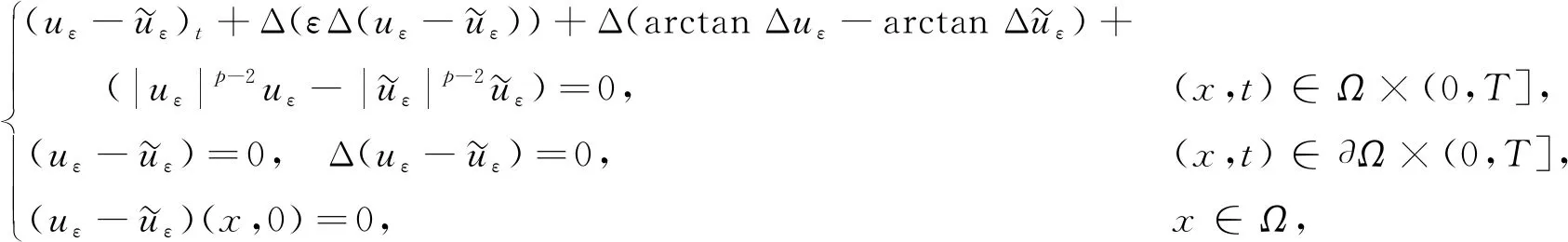
(25)

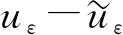
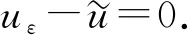
下面证明定理1. 由定理3知

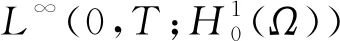
令ε→0, 根据文献[10]得

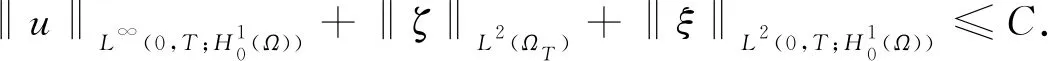
(27)

在式(18)中令ε→0, 可得

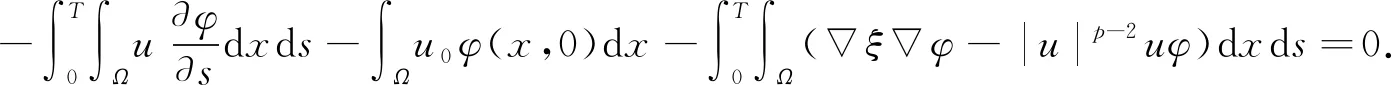
(28)

(29)

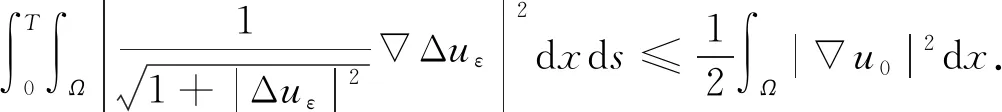
(30)

令ωε=Δuε, 由||ωε||≤|ωε|, 得

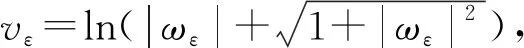
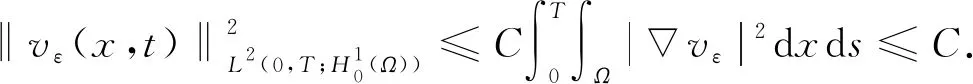
(31)

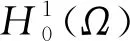
此外, 对任意的δ>0有不等式

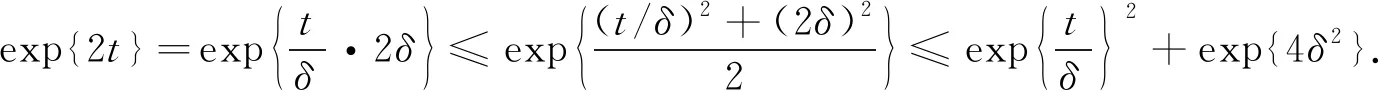
(32)

在不等式(32)中取t=vε和δ=C1‖vε‖L2(ΩT), 可得

又因为

故有

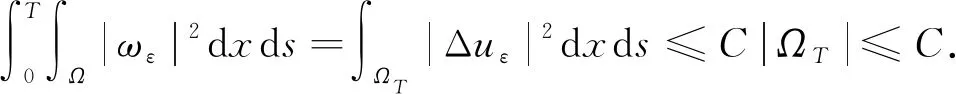
(33)

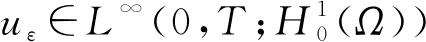
由u满足式(28)知, 要证明u为问题(1)的弱解, 只需证明在ΩT上几乎处处有ξ=arctan Δu. 取u作为式(28)的检验函数且令h→0, 可得

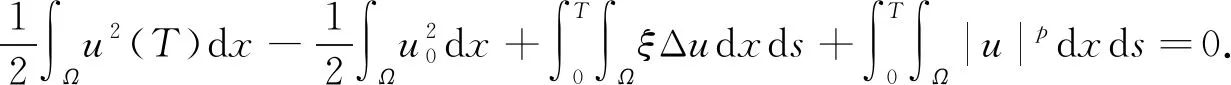
(34)

令ε→0且注意到

可得

结合式(34)知

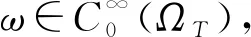
故在ΩT上几乎处处有ξ=arctan Δu. 从而证明了u为问题(1)的弱解.

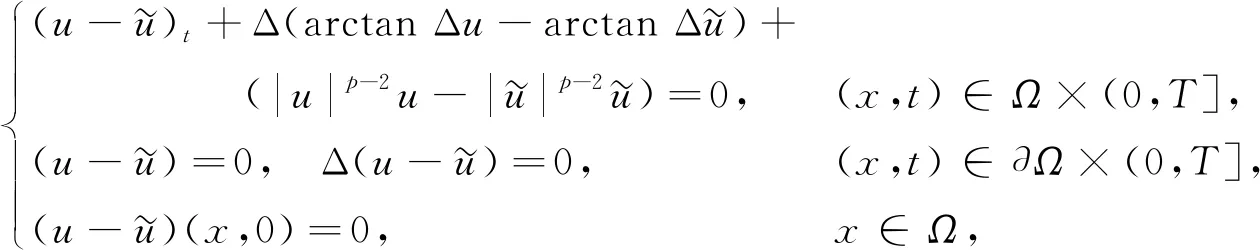
(35)