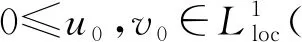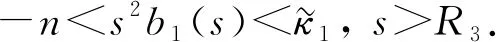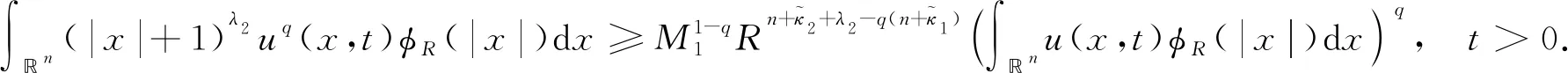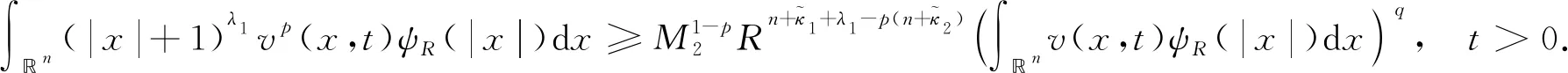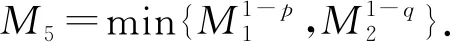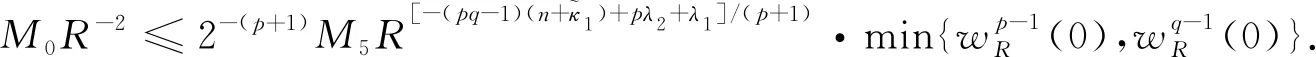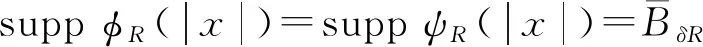一类耦合半线性扩散方程组的Fujita临界曲线
2020-07-17周倩,那杨,高冬
周 倩, 那 杨, 高 冬
(1. 吉林大学 数学学院, 长春 130012; 2. 长春工业大学 数学与统计学院, 长春 130012;3. 吉林大学 计算机科学与技术学院, 长春 130012)
0 引 言
考虑如下耦合半线性扩散方程组Cauchy问题解的整体存在与爆破性质:
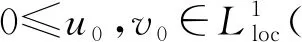

(4)

(5)
且当-n<κ1,κ2≤+∞时,b1,b2满足
κ0=inf{s(s+1)b1(s),s(s+1)b2(s):s>0}>-n.
(6)
本文给出问题(1)-(3)的Fujita临界曲线, 并建立Fujita型定理.
Fujita[1]研究了如下半线性热传导方程的Cauchy问题:
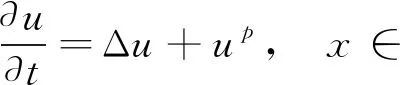
结果表明, 反应项指数p对上述问题解的性质会产生直接影响: 当1
易见Fujita临界曲线关于λ1是单调递增的, 关于κ1是单调递减的, 并在κ1=+∞处退化为1. 表明反应项和一阶项对解的长时间行为均会产生直接影响. 本文研究更一般的问题(1)-(3), 证明问题(1)-(3)的Fujita临界曲线与空间维数κ1,κ2,λ1,λ2有关, 表达式为
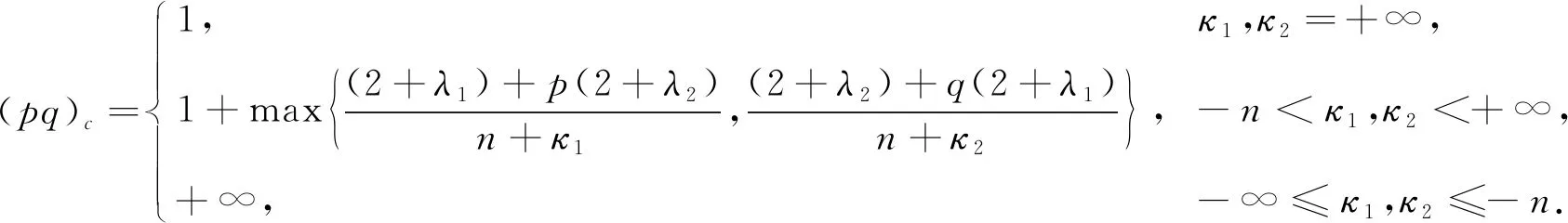
(7)
这里并未给出min{κ1,κ2}≤-n 本文用加权能量积分比较方法证明问题(1)-(3)解的爆破性质, 通过构造恰当的自相似上解, 再结合比较原理证明解的整体存在性. 与文献[20]相比, 本文的难点在于方程组(1)-(2)中一阶项系数和反应项系数都是不一致的. 因此, 不能像文献[20]一样选择相差常数的同类型权函数, 而需要根据不同的系数寻找不同类型的权函数, 再通过适当地伸缩使两个解的能量积分处于同一增长阶, 并且本文需要比文献[20]中更细致的积分估计来计算扩散项、 一阶项和反应项之间的能量关系. 此外, 方程组(1)-(2)的两个对流项系数和反应项系数各不相同, 使得问题(1)-(3)的自相似上解具有更复杂的结构和更细致的运算. 引理1设p,q>1,λ1,λ2≥0,b1,b2∈C1([0,+∞))满足式(4),(5), -n<κ1,κ2<+∞或-∞≤κ1,κ2≤-n, (u,v)是问题(1)-(3)的一个整体解. 则存在仅依赖于n,b1,b2的常数R0>0,δ>0,M0>0, 使得对任意的R>R0, 都有 这里 证明: 易验证φR,ψR∈C1([0,+∞))∩C2((0,R)∪(R,δR)∪(δR,+∞)). 在式(1),(2)两端分别乘以φR,ψR, 然后在n上分部积分得 直接计算可知, 当0<|x| 当R<|x|<δR时, 有 下面假设-n<κ1,κ2<+∞. 由式(4)及-n<κ1<+∞可知, 存在R1>0, 使得 0 (16) 其中M1=(δ1-1)-2π2. 同理由式(5)和-n<κ2<+∞可知, 存在R2>0, 使得 0 (18) 其中M2=(δ2-1)-2π2. 令M0=max{M1,M2},R0=max{R1,R2}, 则将式(12),(17)代入式(10), 即可得式(8), 而将式(13),(19)代入式(11)即证明了式(9). 对于-∞≤κ1,κ2≤-n的情形可类似证明. 证毕. 下面构造方程组(1)-(2)具有如下形式的自相似上解: u(x,t)=(t+τ)-αU[(t+τ)-1/2(|x|+1)],x∈n,t≥0, (20) v(x,t)=(t+τ)-βV[(t+τ)-1/2(|x|+1)],x∈n,t≥0, (21) 则由式(20)和式(21)定义的(u,v)是方程组(1)-(2)的一个上解. 引理2设p,q>1,λ1,λ2>0,b1,b2∈C1([0,+∞))满足式(4)~(6), -n<κ1,κ2≤+∞. 令 U(r)=εe-A(r),V(r)=εe-B(r),r≥0, (24) 其中:ε>0,A,B∈C1([0,+∞))满足A(0)=B(0)=0, 并且 这里0 并且-n<κ3<κ4<κ1, -n<κ5<κ6<κ2满足κ3,κ5<κ0, (n+κ4)[pq+(pq)c-2]>2(p+1)+λ1+λ2p, (n+κ6)[pq+(pq)c-2]>2(q+1)+λ2+λ1q. 则当pq>(pq)c时, 存在0 证明: 易验证U,V∈C1,1([0,+∞)). 对于0 因此, 存在0 由A的定义可知, 由B的定义可知, 因此, 存在0 当r>l时, 通过计算可知, 同理, 当r>l时, 有 对固定的0 由式(26)~(32)可知, 对于r∈(0,l2)∪(l2,l)∪(l,+∞),t>0, 有 由A,B的定义得 选取充分小的ε1,ε2>0, 使得 于是, 根据式(33),(34)可知, 对于r∈(0,l2)∪(l2,l)∪(l,+∞),t>0, 式(22),(33)成立. 因此, 由式(20),(21),(24)定义的(u,v)是方程组(1)-(2)的一个上解. 证毕. 由抛物型方程组的经典理论可知, 问题(1)-(3)存在唯一的局部解且比较原理成立. 下面建立问题(1)-(3)的Fujita型定理. 定理1设p,q>1,λ1,λ2≥0,b1,b2∈C1([0,+∞))满足式(4)~(6), -n<κ1,κ2<+∞或-∞≤κ1,κ2≤-n, 且当-n<κ1,κ2<+∞时, 证明: 只证明-n<κ1,κ2<+∞的情形, 当-∞≤κ1,κ2≤-n时可类似证明. 设(u,v)是问题(1)-(3)的一个整体解. 根据-n<κ1,κ2<+∞和pq<(pq)c可知, (35) (36) 其中:χ[0,δR]是区间[0,δR]上的示性函数;M3,M4>0是不依赖R的常数. 本文只给出[(2+λ1)+p(2+λ2)]/(n+κ1)>[(2+λ2)+q(2+λ1)](n+κ2)的证明, 其他情形的证明类似. 定义 其中 根据引理1可知, 对于任意R>max{R0,R5}, 有 利用Hölder不等式和式(37)可得, 其中M1>0是不依赖R的常数. 即 (40) 同理, 利用Hölder不等式和式(38)可得 (41) 将式(40),(41)代入式(39)得 由θ的定义可知 将式(43)代入式(42)可得 (45) 则根据式(44),(45)可知, 对于任意的R>max{R0,R5,R6}, 有 由于p,q>1, 故存在T*>0, 使得 因此, (u,v)一定在有限时刻爆破. 证毕. 定理2设p,q>1,λ1,λ2≥0,b1,b2∈C1([0,+∞))满足式(4)~(6), -n<κ1,κ2≤+∞. 则当pq>(pq)c时, 问题(1)-(3)既存在爆破解也存在非平凡整体解. 证明: 由引理2和比较原理可直接得问题(1)-(3)在小初值时存在非平凡整体解. 下面讨论问题(1)-(3)解的爆破性质. 对于固定的R>R0, 定义 其中(u,v)是问题(1)-(3)的解. 利用引理1和Hölder不等式可知, 其中 是仅依赖于n,δ,p,q,R的正常数. 当(u0,v0)足够大时, 则由式(46)可知 再根据定理1最后的证明可知, (u,v)一定在有限时刻爆破. 证毕.1 辅助引理
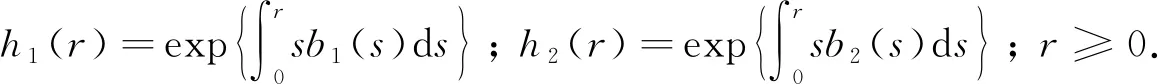

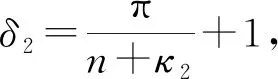
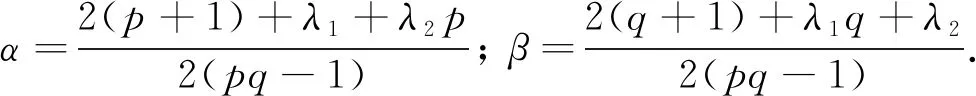
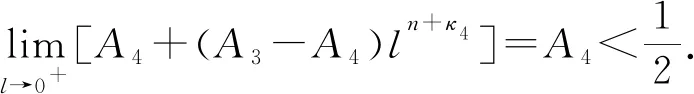
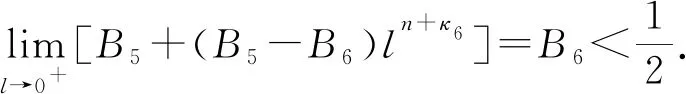
2 Fujita型定理