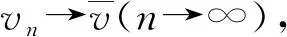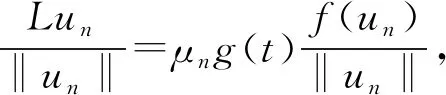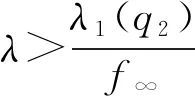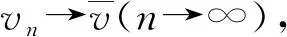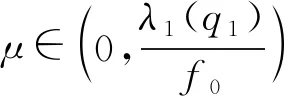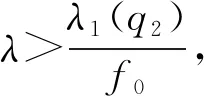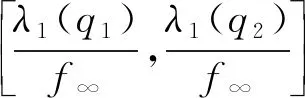一类二阶非线性周期边值问题正解集的全局结构

2020-07-17贾凯军

吉林大学学报（理学版） 2020年4期

贾凯军

(西北师范大学数学与统计学院, 兰州 730070)

0 引言

周期边值问题是常微分方程的经典问题之一, 关于其正解的存在性研究已引起广泛关注. 近年来, 运用锥上的不动点定理、不动点指数理论和临界点理论等工具研究二阶微分方程周期边值问题, 已获得了很多结果[1-11]. 特别地, Graef等[5]用Krasnoselskii’s不动点定理获得了二阶周期边值问题:

(1)

文献[5]在势函数为常函数的情形下, 用锥上的不动点定理获得了问题(1)正解的存在性结果, 但未得到关于其正解集全局结构的任何信息, 因此即使知道了多个解的存在性, 也无法说明这些解是否在一个连通分支上; 文献[6]在势函数为常函数的情形下用点分歧理论得到了问题(1)正解集的分歧行为, 而当势函数进一步推广为q(t)且变系数时, 能否建立类似于文献[6]的结果未知. 事实上, 这会给证明带来新的困难, 目前对此类问题的研究尚未见文献报道. 基于此, 本文用区间分歧理论与拓扑度理论研究二阶周期边值问题：

(2)

正解集的全局结构, 其中λ是一个正参数.

本文总假设:

(H1)q∈C([0,2π],[0,∞))且q(t)不恒为0, 存在两个正常数q1,q2, 使得对任意的t∈[0,2π], 有q1≤q(t)≤q2;

(H2)g∈C([0,2π],[0,∞))且存在t0∈[0,2π], 使得g(t0)>0;

(H3)f∈C([0,∞),[0,∞))且当s>0时,f(s)>0;

参照文献[6], 记λ1(q1)是线性特征值问题:

(3)

的主特征值,φ∞是λ1(q1)对应的非负特征函数. 记λ1(q2)是线性特征值问题:

(4)

的主特征值,φ∞是λ1(q2)对应的非负特征函数.

1 预备知识

注1特别地, 当势函数q(t)=ρ2(ρ>0)时, 问题(2)将退化为文献[5-6]中的问题, 且格林函数退化为

令Σ⊂+×X为问题(2)正解集的闭包. 对于λ≥0, 问题(2)等价于算子方程u=Pu, 其中P:X→X定义为

根据λ,G,g,f的正性可知, 对于任意的t∈[0,2π],u(t)>0, 问题(2)非平凡解(λ,u)的闭包在+×X上恰是Σ. 由条件(H4), 令ξ,ζ∈C(,), 且使得f(u)=f0u+ξ(u),f(u)=f∞u+ζ(u). 显然有

定义算子L:D(L)⊂X→X为Lu=-u″+qu,u∈D(L), 其中

D(L)={u∈C2[0,2π]|u(0)=u(2π),u′(0)=u′(2π)},

则L-1是紧算子. 令关于f的Nemytskii算子N:X→X为N(u)(t)=g(t)f(u(t)),u∈X, 则问题(2)等价于算子方程

u=λL-1N(u),u∈X.

(5)

定义映射Φλ:X→X为Φλ(u)=u-λL-1N(u). 对于任意的R>0, 令BR={u∈X: ‖u‖

引理1[12]设V是一个实的自反Banach空间,F:×V→V是全连续的, 使得F(λ,0)=0, ∀λ∈. 设a,b∈(a

u-F(λ,u)=0,u∈V

(6)

的孤立解, 其中(a,0),(b,0)不是方程(6)的分歧点. 进一步, 假设

deg(I-F(a,·),Br(0),0)≠deg(I-F(b,·),Br(0),0),

其中Br(0)是平凡解的孤立邻域. 设

引理2[13]设V是一个实的自反Banach空间, 令F:×V→V是全连续的. 设a,b∈(a0, 使得对任意的u且‖u‖≥R, 有F(a,u)≠u≠F(b,u). 进一步, 假设当R(R>0)充分大时, 有

deg(I-F(a,·),BR(0),0)≠deg(I-F(b,·),BR(0),0),

则存在方程(6)的一个闭的连通分支C在[a,b]×V中无界, 并且下列条件之一成立:

1) C在λ方向是无界的;

2) 存在区间[c,d], 使得(a,b)∩(c,d)=Ø, 且C在[c,d]×V中从无穷远处产生分歧.

引理3假设条件(H1),(H2)成立, 则λ1(q1)≤λ1(q2).

(7)

(8)

将式(7),(8)相减后再对t从0到2π积分, 并结合边界条件可得

因为u1,u2均大于零,g非负且q2-q1≥0, 所以λ1(q2)≥λ1(q1).

2 主要结果

定理1假设(H1)～(H4)成立, 则:

3) 存在λ*>0, 使得当λ>λ*时, 问题(2)没有正解, 此时Σ∞=Σ0.

考虑下列周期边值问题：

显然, 存在两个正常数q1=1,q2=2且q(t)满足条件(H1),g(t)满足条件(H2), 易知f0=1/2,f∞=2, 则f(u)满足条件(H3),(H4). 通过计算可求出线性特征值问题(3),(4)的主特征值分别为λ1(q1)=1,λ1(q2)=2, 由定理1可知, [1/2,1]和[2,4]分别是该问题的正解从无穷远处与平凡解线上产生的分歧区间, 即1)～3)成立.

下面证明定理1.

1) 证明从无穷远处产生的分歧.

引理4如果Λ是+上的一个紧子区间, 并且则存在R1>0, 使得对任意λ∈Λ有Φλ(u)≠0, ∀u∈X, ‖u‖≥R1.

(9)

Lun=μng(t)f(un),

(10)

(11)

由φ∞,φ∞分别是问题(3),(4)对应于λ1(q1),λ1(q2)的非负特征函数, 并且通过分部积分可得

(12)

即

证明: 由引理4, 对于区间Λ=[0,μ], 存在R1>0, 使得当R≥R1时, 有u-τμL-1N(u)≠0,u∈X, ‖u‖≥R,τ∈[0,1]. 从而对任意的R≥R1, deg(Φμ,BR,0)=deg(I,BR,0)=1.

证明: 反设存在序列{un}⊂X, 使得‖un‖→∞(n→∞), 且当τn≥0时, 有Φλ(un)=τnφ∞, ∀n∈, 则

Lun=λN(un)+τnL(φ∞).

(13)

因为在[0,2π]上τnL(φ∞)≥0, 所以对任意的t∈[0,2π]有un>0. 注意到un∈D(L)存在唯一的分解

un=ωn+snφ∞,

(14)

其中sn∈且〈ωn,g(t)φ∞〉=0. 又由于在[0,2π]上un>0, 结合式(14)可得sn>0, 所以

证明: 由引理5可知, 存在R2>0使得Φλ(u)≠τφ∞, ∀u∈X, ‖u‖≥R2,τ∈[0,1]. 因此, 对任意的R≥R2, 有deg(Φλ,BR,0)=deg(Φλ-φ∞,BR,0)=0.

证明: 对给定的n∈且令取其中R1,R2分别由推论1和推论2定义. 易验证对任意的引理2的所有条件均满足, 因此存在一个闭的连通分支Cn, 并且或者Cn在λ轴的方向上是无界的, 或者存在[c,d]使得(an,bn)∩(c,d)=Ø, 且Cn在[c,d]×X中是从[c,d]×{∞}处分歧出的. 由引理4可知, 后一种情形不会发生. 因此Cn是从[c,d]×{∞}分歧出的, 且Cn在λ轴的方向上无界. 进一步, 由引理4知, 对任意闭子集集合{u∈X|(λ,u)∈Σ,λ∈I}在X中有界, 所以Cn必为从处分歧出的, 并且Cn在λ轴的方向上无界.

由命题1可知, 定理1中结论1)成立.

2) 证明在平凡解线上产生的分歧.

引理6如果Λ是+上的一个紧子区间, 并且则存在δ1>0, 使得对任意λ∈Λ有Φλ(u)≠0, ∀u∈X， 0<‖u‖≤δ1.

(15)

由φ∞,φ∞分别是问题(3),(4)对应于λ1(q1),λ1(q2)的非负特征函数及式(12)可得

证明: 由引理6知, 对于区间Λ=[0,μ], 存在δ1>0使得当0<‖u‖≤δ1时, 有u-τμL-1N(u)≠0,u∈X, 0<‖u‖≤δ1,τ∈[0,1]. 从而对任意的δ∈(0,δ1), deg(Φμ,Bδ,0)=deg(I,Bδ,0)=1.

证明: 反设存在序列{un}⊂X, 使得‖un‖→0(n→∞), 且当τn≥0时, 有Φλ(un)=τnφ∞, ∀n∈, 则式(13)成立. 显然un>0且un∈D(L)存在唯一的分解式(14), 其中sn∈且〈ωn,g(t)φ∞〉=0. 由于在[0,2π]上un>0, 结合式(14)可得sn>0, 所以