高考数学能力小题训练（9）

一、填空题

1.已知集合A=｛x|x2+2x-3＜0｝，B=｛x||x-1|＜2｝，则A∩B=

3.如图是一次考试成绩的样本频率分布直方图，样本容量为2000，若成绩不低于60分为及格，则样本中的及格人数是

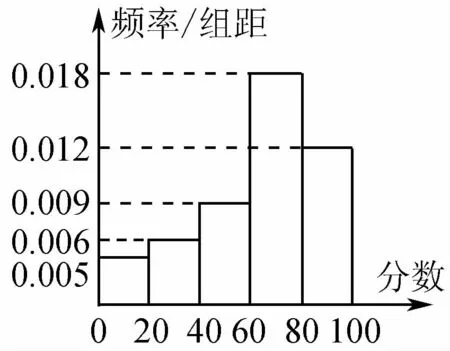
（第3题）

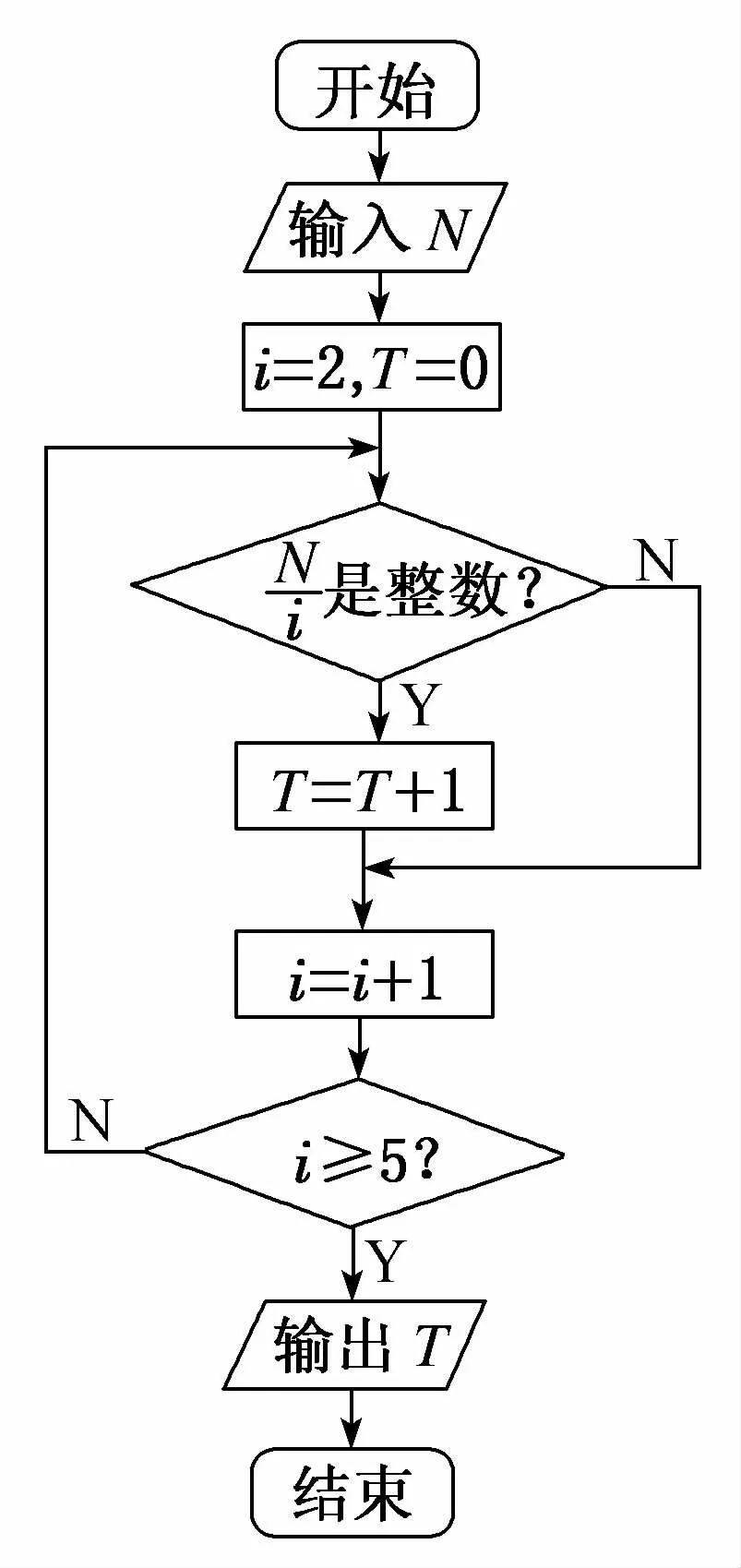
（第4题）

4.（2018年天津高考改编）阅读如图所示的程序框图，运行相应的程序，若输入N的值为20，则输出T 的值为

5.（2020年泰州市联考）现有10个数，它们能构成一个以1为首项，-3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是

6.如图，已知ABCDEF 为正六边形，若经过A，B，D，E 匹点的椭圆恰好以点C，F 为两个焦点，则该椭圆的离心率为

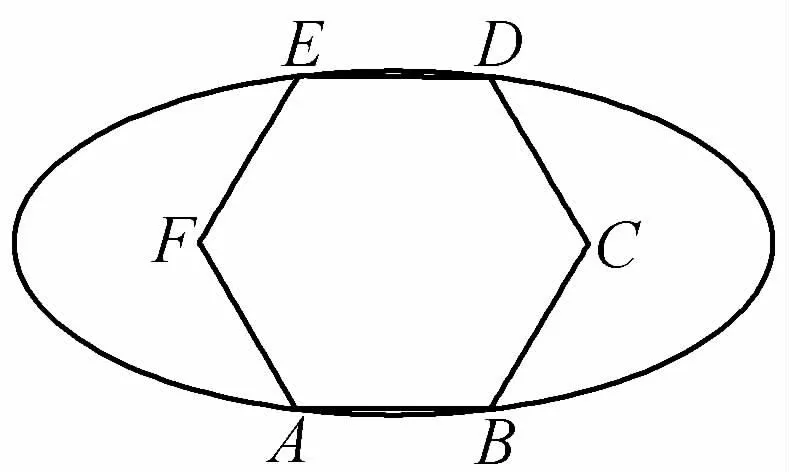
（第6题）

7.在平行匹边形ABCD 中，已知AB=2，AD=1，∠BAD=60°，E 为CD 的中点，则

8.（2019 年重庆一中模拟）若圆x2+y2+2x-6y+6=0上有且仅有三个点到直线x+ay+1=0的距离为1，则实数a的值为

10.已知奇函数f（x）=5x+sinx+c，x∈（-1，1），如果f（1-t）+f（1-t2）＜0，则实数t的取值范围为

11.我国古代数学名著《九章算术》中割圆术有：“割之弥细，所失弥少，割之又割，以至于不

可割，则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程，比如在中“…”即代表无限次重复，但原式却是个定值x，这可以通过方程x确定x=2，则

12.已知a，b为正数，且直线ax+by-6=0与直线2x+（b-3）y+5=0互相平行，则2a+3b的最小值为

13.已知Sn是数列｛an｝的前n项和，若Sn=1-nan（n∈N*），则Sn关于n 的表达式为Sn=

14.设点P在曲线y=x2+2上，点Q在曲线上，则|PQ|的最小值为

二、解4题

（1）PA⊥底面ABCD；

（2）BE∥平面PAD；

（3）平面BEF⊥平面PCD.

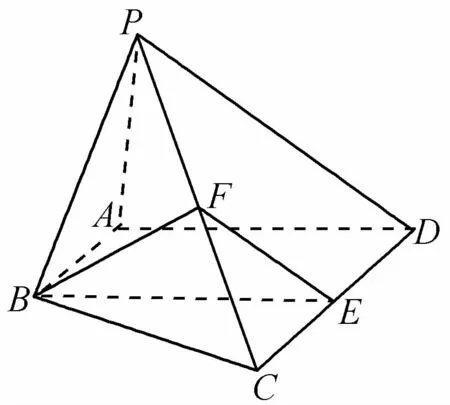
（第15题）

16.（2016年广州高中综合测试）已知数列｛an｝的前n项和为Sn，数列是首项为1，公差为2的等差数列.

（1）求数列｛an｝的通项公式；

（2）设数列｛bn｝满足求数列｛bn｝的前n 项和Tn.