高考数学能力小题训练（7）

一、填空题

1.若集合A=｛x|y2=x，y∈R｝，B=｛y|y=sinx，x∈R｝，则A∩B=

4.方程log2（9x-5）=2+log2（3x-2）的解x=

5.掷两颗骰子得两个数，若两数的差为d，则d∈｛-2，-1，0，1，2｝出现的概率的最大值为.（结果用最简分数表示）

6.将函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象向左平移个单位长度，所得函数的图象与函数y=f（x）的图象关于x轴对称，则ω的最小值为

7.（2020年镇江市联考）在△ABC 中，已知c=2，若sin2A+sin2B-sinAsinB=sin2C，则a+b的取值范围为

8.（2019年德州模拟）已知圆C 的圆心在x 轴的正半轴上，点M（0）在圆C 上，且圆心到直线2x-y=0的距离为，则圆C的标准方程为

9.如图，在直三棱柱ABC A1B1C1中，∠ABC=90°，AB=BC=1，若A1C 与 平 面B1BCC1所 成的角为，则三棱锥ABC的体积为

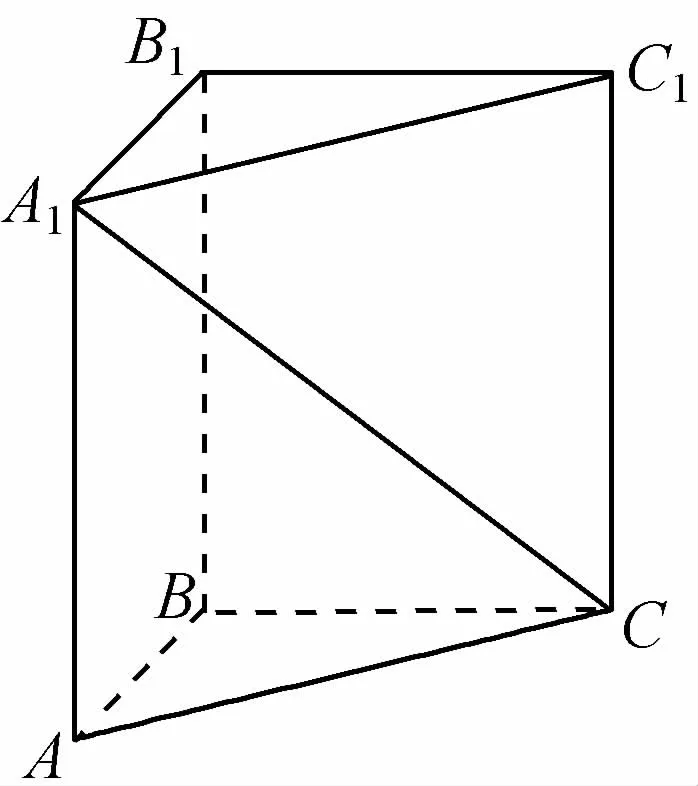
（第9题）

10.（2019年武汉调研）函数f（x）=Acos（ωx+φ）（ω＞0）的部分图象如图所示，给出以下结论：

（1）f（x）的最小正周期为2；

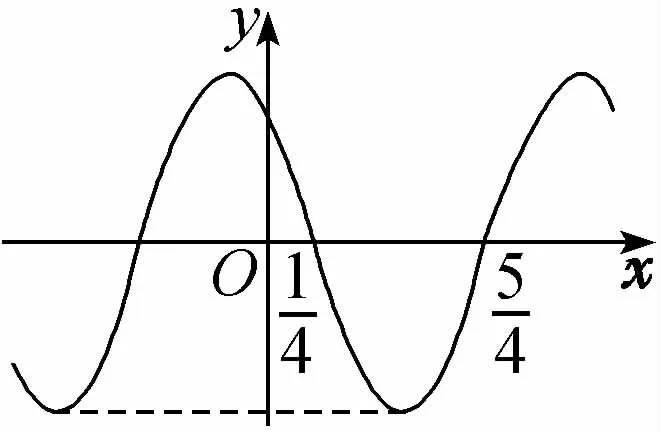
（第10题）

（4）f（x）的最大值为A.

11.对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”：

依此类推，若m3的“分裂数”中有一个是2019，则m=

12.设θ是两个非零向量a，b的夹角，若对任意实数t，|a+tb|的最小值为2，则|a|的最小值为

13.已知定义域为R的函数y=f（x）满足f（x+2）=f（x），且-1≤x＜1时，f（x）=1-x2，函 数若F（x）=f（x）-g（x），则当x∈[-5，10]时，函数F（x）零点的个数是

14.数列｛an｝满足：an-1+an+1＞2an（n＞1，n∈N*），给出下述命题：

①若数列｛an｝满足：a2＞a1，则an＞an-1（n＞1，n∈N*）成立；

②存在常数c，使得an＞c（n∈N*）成立；

③若p+q＞m+n（其中p，q，m，n∈N*），则ap+aq＞am+an；

④存在常数d，使得an＞a1+（n-1）d（n∈N*）都成立.

二、解4题

（1）平面ADE⊥平面BCC1B1；

（2）直线A1F∥平面ADE.

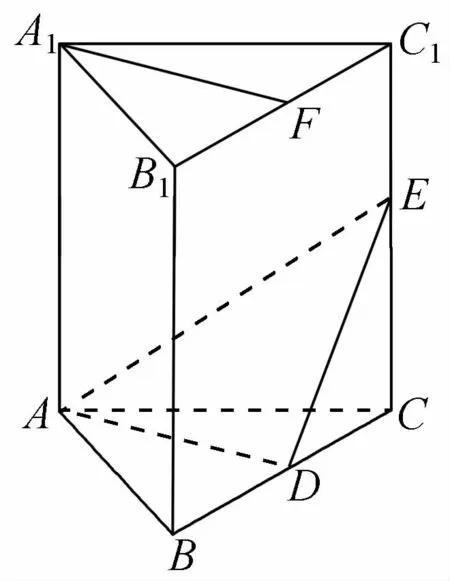
（第15题）

16.已知数列｛an｝的各项均为正数，满足a1=1，ak+1-ak=ai（i≤k，k=1，2，3，…，n-1）.

（1）求证：ak+1-ak≥1（k=1，2，3，…，n-1）；

（2）若｛an｝是等比数列，求数列｛an｝的通项公式；

（3）设数列｛an｝的前n项和为Sn，求证：