解析几何中的定值问题

一、填空题

1.已知A（x1，y1），B（x2，y2）是抛物线y2=2x上两点，且0A⊥0B，则y1y2=.

2.如图，半圆的直径AB=6，0为圆心，C为半圆上不同于A，B的任意一点，若P为半径0C上的动点，则的最小值是________..

（第2题）

3.已知AB是经过椭圆b＞0）右焦点的任意一条弦，若过椭圆中心0的弦MN∥AB，则|MN|2：|AB|恒等于________..

4.（2019年泰州市模拟卷）已知A，B，P是椭圆上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率乘积，则该椭圆的离心率为________.

5.已知正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线y2=2x上，则这个正三角形的面积为________..

6.（2020年苏州市期末卷）设M为双曲线上的任意一点，则点M到双曲线的两条渐近线的距离之积为________.

7.一束光线从A（-1，1）出发，经x轴反射到圆（x-2）2+（y-3）2=1上的最短路程为________.

8.设a，b是关于x的方程x2sinθ+xcosθ-2=0的两个实根（θ∈R，a≠b），直线l过点A（a，a2），B（b，b2），则坐标原点0到直线l的距离是________..

9.已知圆0：x2+y2=8交x轴于A，B两点，M是直线x=-4上的任意一点，以0M为直径的圆K与圆0相交于P，Q两点，则直线PQ必过定点________.

10.（2019年海安练习卷）已知圆0：x2+y2=1，点P在直线l：2x+y-3=0上，M为直线y=x与直线l的交点，若在平面内存在定点N（不同于点M），满足：对于圆0上任意一点Q，都有为定值，则定点N的坐标为________.，定值为________.

二、解答题

11.已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线的焦点，离心率等于.

（1）求椭圆C的方程；

（2）过椭圆C的右焦点F作直线l，交椭圆C于A，B两点，交y轴于点M，若，求证：λ1+λ2为定值.

12.已知椭圆C：的两个焦点分别为，点M（1，0）与椭圆短轴的两个端点的连线相互垂直.

（1）求椭圆C的方程；

（2）过点M（1，0）的直线l与椭圆C相交于A，B两点，设点N（3，2），记直线AN，BN的斜率分别为k1，k2，求证：k1+k2为定值.

13.若椭圆C：的离心率e为，且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.

（1）求椭圆C的方程；

（2）设点M（2，0），点Q是椭圆上一点，当MQ最小时，试求点Q的坐标；

（3）设P（m，0）为椭圆C长轴（含端点）上的一个动点，过P点斜率为k的直线l交椭圆于A，B两点，若PA2+PB2的值仅依赖于k而与m无关，求k的值.

（第13题）

14.（2020年海门中学练习卷）在平面直角坐标系x0y中，椭圆C：的左顶点为A，点P，Q是椭圆C上的两个动点.

（1）如图，当P，0，Q三点共线时，直线PA，QA分别与y轴交于M，N两点，求证：为定值；

（2）设直线AP，AQ的斜率分别为k1，k2，当k1·k2=-1时，求证：直线PQ经过定点R.

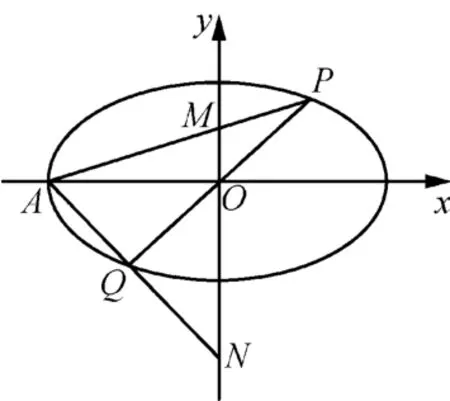
（第14题）