数学文化融入高考试题(二):展示中国数学成就
2020-07-16李双双
李双双
同学们,我们来谈一谈数学文化融入高考试题的另一种方式——展示中国数学成就.在高考试题中,经常会出现以中国数学家的研究成果或中国历史上的数学研究著作为素材、结合数学知识和原理命制的试题,再现我国数学家和劳动人民在数学上所取得的成果,体现我国劳动人民和科学家的勤劳与智慧,在培养同学们勇于实践、不断创新的精神的同时,进行爱国主义教育.
一、典型试题分析
(一)与中国数学家有关的试题
例1(2018年全国Ⅱ理科卷)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2 的偶数可以表示为两个素数的和”,如30=7+23.在不超过30 的素数中,随机选取两个不同的数,其和等于30 的概率是( ).
◆【分析】首先要知道素数的概念,素数是“只能被它自身和1 整除的、不小于2 的整数”,本题的难点在于列举出不超过30 的所有素数,理解这是一个古典概型的概率模型.首先由列举法先求出不超过30 的所有素数:2,3,5,7,11,13,17,19,23,29,共10 个.从这10 个数中随机选取2 个不同的数有种选法,其中,和等于30 的数对有:7 和23,11 和19,13 和17,共3 对.所以在不超过30 的素数中,随机选取两个不同的数,其和等于30 的概率为.故答案选C.
小知识

陈景润(1933.5.22—1996.3.19),师从于华罗庚,1973年在《中国科学》杂志上发表了“1+2”的详细证明,被公认为是对哥德巴赫猜想研究的重大贡献.他的成果被国际数学界称为“陈氏定理”.
世界近代三大数学难题:哥德巴赫猜想、费马猜想和四色猜想.后两者已被证明,现在我们称之为费马大定理、四色定理;但哥德巴赫猜想尚未被完全证明,等着同学们去探索哦!
解题回顾
本题一方面从知识角度考查古典概型这样一个重要的概率模型,另一方面,是为了通过我国当代数论专家陈景润所取得的重大研究成果,激励同学们不断学习、勇攀科技高峰,为国家的发展和中华民族的伟大复兴贡献聪明和才智.
例2(2019年浙江卷)祖暅是我国南北朝时期的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图1所示,则该柱体的体积是( )
A.158 B.162 C.182 D.32
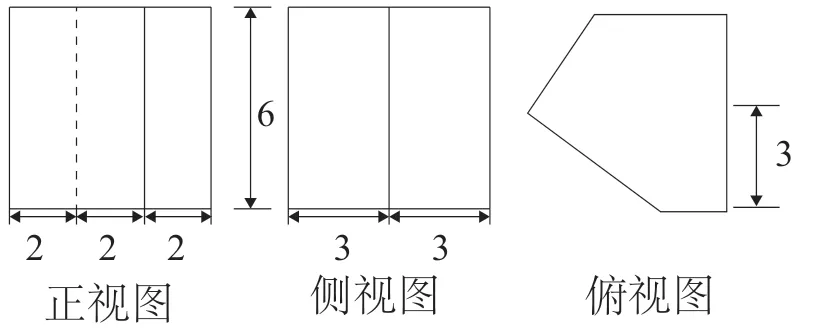
图1
◆【分析】由正视图得该棱柱的高为6.由俯视图可知,其底面可以看作是由两个直角梯形组合而成的(如图2):其中一个上底为4,下底为6,高为3;另一个上底为2,下底为6,高为3.所以该柱体的底面积为,故该柱体的体积为27×6=162.故选B.
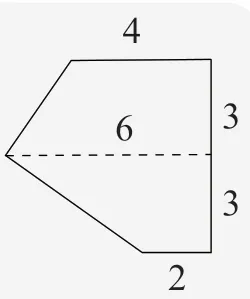
图2
解题回顾
本题的解题关键是要能够根据三视图,还原得到几何体——棱柱,确定棱柱底面的形状为两个直角梯形拼成的图形(如图2),然后再由柱体体积公式V柱体=Sh计算出柱体的体积.本题难度较低,除了考查三视图等立体几何知识外,还为了让同学们了解祖暅原理等中国古代数学文化.
敲黑板
古典概型的概率计算公式比较简单.那么你还记得什么是古典概型吗?
小知识
祖暅(456—536),中国南北朝时期著名的数学家、天文学家,在求球体积时,他使用了祖暅原理:“幂势既同,则积不容异.”其中“幂”是截面积,“势”是几何体的高(即夹在两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等).这一原理可用来计算一些复杂几何体的体积,例如推导球的体积公式.
国外则一般称之为卡瓦列里原理,在西方,意大利数学家卡瓦列里(Cavalieri.B)于1635年提出了等积原理,他的这一发现要比我国的祖暅晚1100 多年.
同学们到大学里学习定积分后,对这个结论的认识就会更深刻啦!
(二)与中国数学著作有关的试题
例3(2018年上海卷)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设AA1是正六棱柱的一条侧棱,如图3所示.若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马个数是( ).
A.4 B.8 C.12 D.16
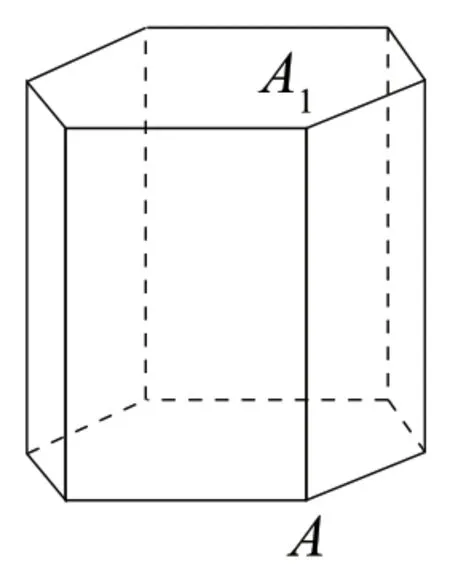
图3
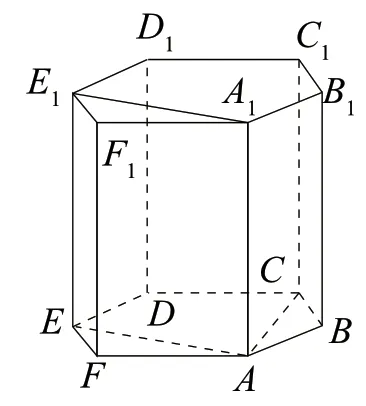
图4
◆【分析】如图4,在正六边形ABCDEF中,EA⊥AB,DB⊥AB,由正六棱柱的性质可知,AA1⊥平面ABC,所以EA⊥AA1,DB⊥AA1,所以EA⊥平面AA1B1B,DB⊥平面AA1B1B;又由E1A1∥EA,D1B1∥DB,得E1A1⊥平面AA1B1B,D1B1⊥平面AA1B1B.所以,以矩形AA1B1B为底面的阳马有4 个.同理,以矩形AA1F1F为底面的阳马也有4 个;类似地,以矩形AA1C1C为底面的阳马有4 个,顶点分别是D,D1,F,F1;同理,以矩形AA1E1E为底面的阳马也有4 个.
所以,阳马的总数为16 个.故选答案D.
解题回顾
本题是一道立体几何新概念题,旨在考查阅读理解能力、逻辑推理能力和空间想象能力,并渗透中国古代数学文化.解题时,首先要理解新概念“阳马”:它是一个四棱锥,底面是矩形,且有一条侧棱垂直于底面;然后再去找四棱锥的底面——AA1为一边的矩形,共有4 个,分别是AA1B1B,AA1F1F,AA1C1C,AA1E1E(想一想:为什么AA1D1D不行呢?);再找分别与这4 个底面垂直的四棱锥的侧棱,各有4 个,所以一共有16 个.
敲黑板
本题中,很多同学遗漏了以矩形AA1C1C和AA1E1E为底面的阳马,从而错选A 或B.
你是不是也掉坑了呢?
小知识
取一长方体,按下图斜割一分为二,得两个一样的三棱柱,称为堑堵.
再沿堑堵的一顶点与相对的棱剖开,得四棱锥和三棱锥各一个.以矩形为底,另有一棱与底面垂直的四棱锥,称为阳马.余下的三棱锥是由四个直角三角形组成的四面体,称为鳖臑.
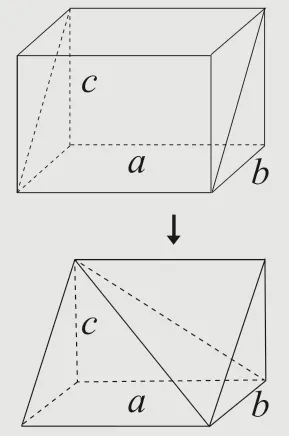
堑堵

阳马
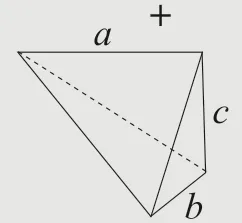
鳖臑
二、解题回顾与反思

同学们在今后的学习过程中,应当关注以下几点:
1.关注我国数学成就,弘扬中华文化
同学们可以利用闲暇时间,浏览我国数学家的数学研究成果(如查找当代数学家华罗庚、陈景润的研究成果,了解祖暅及其家族对中国数学的巨大贡献),适当阅读我国古代的一些高水平的数学著作(如《九章算术》《周髀算经》《孙子算经》等),从而关注我国的数学成就,了解我国历代数学家对数学的贡献,全面了解我国数学和科技发展的大致脉络.
2.提高阅读理解能力,正确理解题意
同学们要有意识地培养自己的阅读理解能力,面对新的内容(数学的,或者非数学的),要认真地、逐字逐句地阅读,并且在读题的同时,动手、动脑.动手,就是在题干上做一些标注,或是通过列表、画图等方式,帮助我们更好地理解题干的本质.如在例3 中,正确地理解“阳马”这一新概念,是我们解决问题的前提.
3.重视数学抽象能力,提升核心素养
在平时的学习过程中,同学们要学会将实际问题抽象为数学问题,理解所要求解问题的本质,并通过相应的数学模型来解决问题.如在例1 中,首先要把问题抽象成一个古典概型的求概率问题,也就需要求出相应的基本事件的个数,再由古典概型的概率公式,得到答案.
三、小试牛刀(原创题)

“分步设问、一题两空”是新高考的又一种新题型:在4道填空题中,有1 道试题采用这种方式命题,通常第一空2 分,第二空3 分.请你试着解下列这道填空题.
我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微;数形结合百般好,隔离分家万事休.”在数学学习过程中,我们经常运用“数形结合”的方法来解决问题,请你尝试着用数形结合的思想方法解决下面的问题:
答案:
①3;②(1,e).
