基于ANSYS的车轮踏面紧急制动热分析*

2020-07-13马晓杰朱绘丽

铁道机车车辆 2020年3期

张野，马晓杰，朱绘丽

(1 新乡学院，河南新乡 453003；2 河南工学院机械工程系，河南新乡 453003)

地铁列车制动系统关系着列车的运行安全，是一个至关重要的系统。地铁车站站间距短，导致列车频繁的牵引制动。轮轨的磨损、剥离等现象，越来越严重。列车制动过程中，车轮表面将产生大量的热，温度越高会使车轮表面材料软化，增加车轮的磨耗损伤，严重影响车轮寿命。而紧急制动作为列车制动最恶劣的一种情况，有必要对其进行研究。

国内外众多研究者都对车轮制动热效应进行了研究。在数值方面，M. Blatnicky等[1]进行了车辆轴结构梁的数值分析，以热流为载荷加载于车轮上，讨论了热流载荷的影响。J. Gerlici等[2]同样对热流进行了分析，主要研究了斜坡制动时制动块内的温度场变化情况。Cameron Lonsdale等[3]就热负荷的问题，研究了重载货车车轮的制动过程。侯耐等[4]针对重载货车，在长大下坡道的紧急制动工况及逆行情况下，对踏面制动热效应进行了研究。在制动过程中，不仅要考虑踏面制动热负荷的情况，还要对踏面应力进行分析。T. Lack等[5]就制动热载荷导致的车轮磨损损伤等问题，采用改进的条带法对车轮的热应力进行评估。向阳等[6]研究了不同车轮轮径下，货车紧急制动时踏面制动热应力变化情况。J. Gerlici等[7]利用试验的方法即利用车辆制动部件试验台测试了其热应力变化情况。在仿真方面，近年来有限元方法为计算车轮制动等现实问题提供了强大的技术支撑。Ahlström等[8]利用对称有限元模型分析了车轮在滑移过程中踏面表面温度的变化情况。尹志凯等[9]利用MARC有限元软件建立了闸瓦和车轮的三维接触模型，讨论了车轮踏面的温度变化情况和应力大小。Naeimi等[10]建立了三维弹塑性有限元模型分析了轮轨接触的温度变化以及踏面应力应变情况。张琪等[11]利用有限元软件建立了不同地铁车轮结构几何参数下的踏面模型，计算了不同模型下制动热负荷的变化情况。Andrej Suchánek等[12]利用有限元软件ANSYS Workbench分析了制动过程中的踏面温度分布情况，并分析了沿径向的应力变化。Teimourimanesh等[13]针对地铁车轮不同辐板进行了研究，主要讨论了温度和疲劳强度等问题。

地铁车辆的频繁制动问题关系着人们出行的安全问题。利用有限元软件ANSYS建立了车轮紧急制动的三维弹性模型，重点针对地铁车辆的闸瓦制动进行研究。该模型采用瞬态热分析方法进行计算，考虑了车轮与闸瓦之间的热传导情况，以及与空气的表面换热情况。就车轮踏面热效应和热应力进行了分析，讨论了表面换热系数和轴重对热效应产生的影响。为车轮紧急制动分析提供了一个直观的结果，也为后续的研究提供了一个具有理论支撑且简单的方法。

1 模型介绍

1.1 基本模型

文中基于有限元软件ANSYS 14.5建立了地铁6B编组的踏面紧急制动车轮模型。如图1所示，该模型以新轮为研究对象，建立真实尺寸的车轮模型，考虑列车最高速度为80 km/h。假设该模型为弹性车轮，暂不考虑其塑性特性。根据文献[12]所提及的计算制动热方法，同样考虑了列车连续两次紧急制动时的车轮踏面热效应情况，并得出相应结果。

1.2 建模方法

利用有限元软件ANSYS进行三维模型建立，选用单元类型SOLID70建立车轮，考虑车轮只具有弹性特性，忽略了不影响计算结果的注油小孔以及结构倒角等。建模过程中，将踏面与闸瓦接触面进行细化处理，达到收敛要求。利用瞬态热分析中的间接法进行热及热应力计算，设置环境温度为20 ℃。首先进行热分析，得到相应的温度场，之后将热分析单元转换为结构分析单元，将温度场作为已知条件进行结构分析。将车轮的轴端面进行约束。

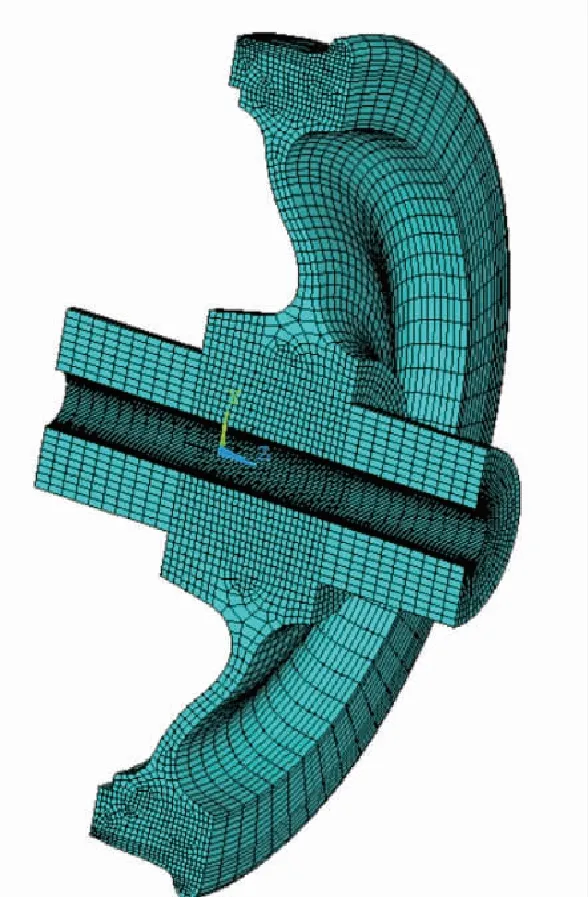
图1 紧急制动车轮模型

1.3 求解方法

利用ANSYS模拟车轮在闸瓦的作用下紧急制动，该过程考虑了车轮与闸瓦间的热传导问题，并以热传导第2类边界条件作为热流输入的边界，即考虑边界上的热流密度，而该函数可能与位置和时间有关。因假设摩擦热在车轮踏面均匀分布，则该函数只与时间有关。其他车轮表面除了轴外均以第3类热传导问题为边界条件[14]，即边界表面传热系数，与时间相关的函数。假设紧急制动过程中，列车动能全部转化为紧急制动热能。一部分能量被车轮和闸瓦吸收，另外一部分被消散在空气当中。被车轮和闸瓦吸收部分又需考虑两者的分配情况，具体公式如式(1)

(1)

式中，λw、λb、aw和ab分别是车轮和闸瓦的导热系数和导温系数。根据文献[15]，取热流分配系数η=0.91。

第2类边界条件即踏面热流密度的具体表达式如式(2)

(2)

式中，Q(t)为制动损失能量；S为踏面摩擦面积。

而与空气之间的交换则要考虑表面换热系数，即第3类热传导问题边界条件，具体表达式如式(3)

h=0.382 8+14.39v(t)

(3)

热流加载方式有两种，即热流加载方式-移动热源法和均布热源法。图2为两种热流加载方式下新轮连续两次紧急制动踏面最高温度时间历程。从图中可以看出，两种热流加载方式得到的结果变化整体趋势一致。采用移动热源法计算的温度分布出现波动现象，这主要是车轮与闸瓦接触的踏面区域，吸收摩擦热，温度上升，而未与闸瓦接触的踏面区域，与空气对流放热，温度下降。而用均布热源法计算，踏面节点温度不随车轮旋转过程波动。由于列车速度较高，两种加载方式结果相差不大，所以文中主要采用均布热源法进行热流加载。图3为均布热源法加载计算的车轮踏面温度分布情况。从图中可以看出，车轮踏面温度沿周向均匀分布。

图2 两种热流加载方式下新轮两次紧急制动踏面最高温度时间历程

图4为车轮与闸瓦热流分配示意图。假设闸瓦如图中的长条形，每一个方格代表一个单元；车轮为图中的同心圆。在考虑均布热源法加载后，车轮表面温度沿周向均匀分布，由于考虑了热流分配系数η=0.91，则车轮以0.91份将热量分走，每次车轮旋转一周，热量累加。若考虑表面换热系数，则车轮0.91份的热量将根据系数大小而散失。

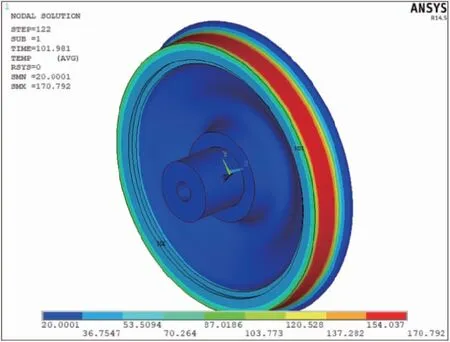
图3 均布热源法加载计算结果

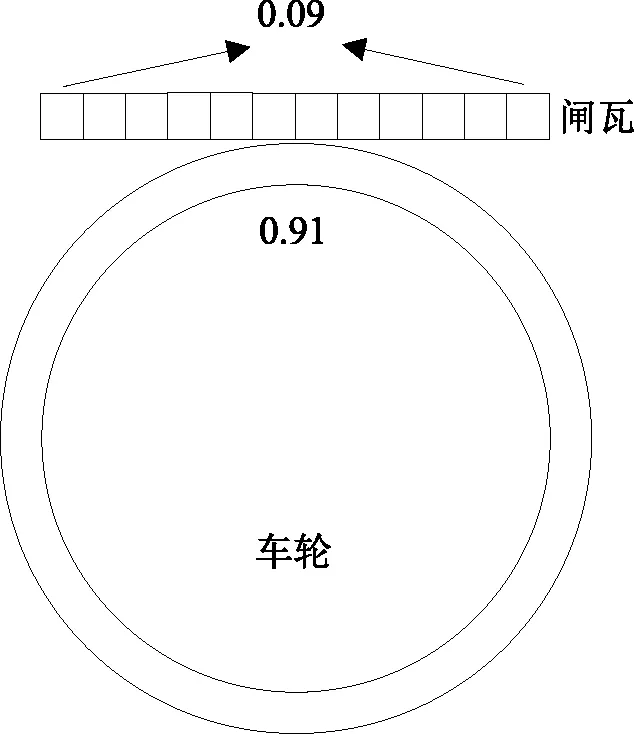
图4 热分布示意图

2 ANSYS热分析

2.1 计算参数

为了求解连续两次紧急制动过程中车轮踏面热分布情况，在ANSYS软件中，利用瞬态热分析求解制动过程，两次紧急制动过程中间相隔30 s。车轮材料的热性能仿真参数如表1所示。

表1 材料的热性能参数

2.2 连续两次紧急制动

基于ANSYS计算所得结果，图5给出了连续两次紧急制动过程中的最高温度云图。经分析可得，最高温度的值出现在第2次紧急制动过程中，温度值为170.792 ℃。从图中可以看出，随着径向深度增加，温度逐渐减小。为了进一步分析温度随时间的变化情况以及随径向深度的变化情况，如图6所示，选取了图5中踏面表面最高温度节点103，以及在截面平面内沿径向分布的节点，得到了如图7所示结果。图7给出了所选节点的温度随时间变化以及沿径向方向的分布情况。从图7中可以看出，第1次紧急制动后，间隔30 s后的第2次紧急制动过程中出现了最高温度。沿着径向深度的增加，不同节点的最高温度也出现在第2次紧急制动过程中。但随着径向深度的增加，温度逐渐减小。闸瓦制动过程中，温度主要集中在车轮踏面表面，对表面材料影响很大，对径向深度影响越来越小。过高的温度易引起材料的软化，硬度变小，很容易导致车轮表面凹痕或擦伤。

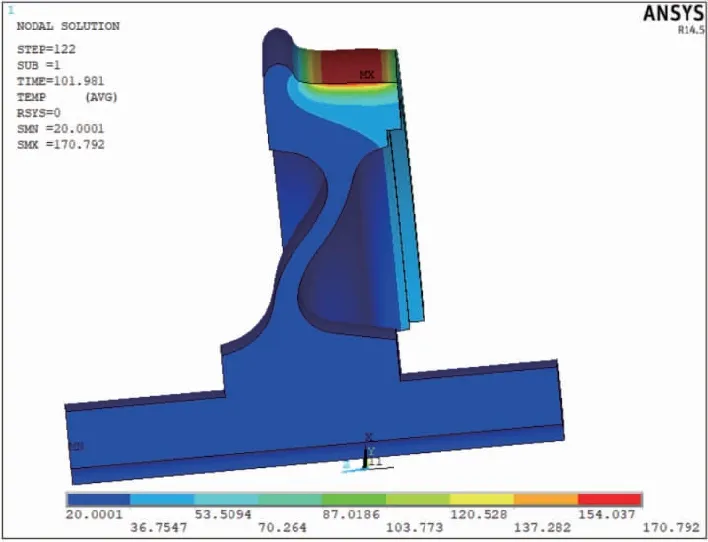
图5 连续两次紧急制动中最高温度云图

图6 用于分析温度随时间变化的节点

2.3 热应力计算

将图5所得温度场当作热载荷参数进行结构热应力的求解，得到如图8所示截面对应的热应力结果。在第2次紧急制动最高温度下车轮踏面等效应力为224 MPa。图8直观地反应了沿着径向深度增加等效应力逐渐减小。图9给出了图6中6个节点在热载荷条件下的等效应力值随着时间的变化情况。从图中可以看出，等效应力有着与温度随时间变化一样的趋势，温度高则对应的等效应力大。但在接近腹板的两个节点上的等效应力值相反，主要是因为腹板属于车轮的薄弱部位，应力较为集中。越接近腹板位置的节点，其等效应力值越大，即节点321的等效应力值大于节点199的等效应力值，此处所得结果与文献[13]类似。温度越高引起的热应力值越大，对车轮表面以及闸瓦表面的材料影响越大，所以闸瓦散热性能的优化设计在后续研究中应进行考虑。

图7 不同节点的温度随时间的变化

图8 节点103热载荷下的等效应力云图

图9 不同节点的等效应力随时间的变化

3 表面换热系数的影响

图10为未考虑表面换热系数连续两次紧急制动中最高温度云图。从图中可以看出，最高温度为171.112 ℃，与之对应的图5为考虑表面换热系数连续两次紧急制动的最高温度云图，其最高温度值为170.792 ℃，两者温度相差0.32 ℃。可见在较高速度情况下，表面换热系数影响不大，即车轮与空气之间的热交换速度不及踏面与闸瓦间的热产生速度。图11为未考虑表面换热系数不同节点的温度随时间的变化，与对应的图7变化趋势相同，最高温度均出现在第2次紧急制动过程中，沿径向深度温度逐渐减小。

图10 未考虑表面换热系数连续两次紧急制动中最高温度云图

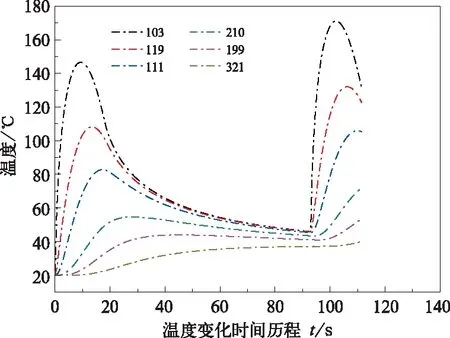
图11 未考虑表面换热系数不同节点的温度随时间的变化

4 轴重的制动热影响

从地铁车辆轻量化设计的角度出发，考虑列车轴重对车轮紧急制动过程中热产生的影响。因此选择了3种不同轴重进行紧急制动计算，即10 t，14 t，18 t。图12为3种轴重工况下踏面表面节点103温度随时间的变化。从图中可以看出，最高温度仍出现在第2次紧急制动过程中，且随着轴重的增加，温度逐渐变大。图13为不同轴重下节点103的等效应力随时间的变化情况。等效应力值也因为轴重的增加，而增大。轴重的增大使温度和等效应力值都有明显的增大，影响明显。可见，列车轻量化设计有利于减少列车车轮制动热，减少车轮踏面的损伤。