动力集中动车组动力车直线运行晃车问题研究*
2020-07-13张志超杜瑞涛储高峰
张志超, 李 谷, 杜瑞涛, 储高峰
(中国铁道科学研究院集团有限公司 机车车辆研究所, 北京 100081)
动力集中动车组是根据我国铁路发展需要自主研发设计的新一代既有干线主要车型,列车动力仅由端部动力车提供。动力车的动力学性能对于整个列车的运行安全性、平稳性以及维护经济性都具有重要影响[1]。在对动力集中动车组样车进行动力学试验过程中发现,动力车在直线工况运行时会出现明显的晃车现象,车体横向加速度存在明显的周期性波动[2]。问题的出现虽然不会对列车运行安全性和其后部载客车辆的运行平稳性产生影响,但是由于动力车运行平稳性的降低,使司机操作人员的工作环境变得恶化,同时也会对动力车关键结构部件的疲劳损伤构成隐患。需要对该问题开展深入的研究分析,提出切实有效的解决方案和措施。
首先系统分析了动力车在历次实车动力学线路试验中的检测数据,研究了该问题与轮轨等效锥度、抗蛇行减振器安装角度的关联性;然后借助于动力学分析软件建立了仿真分析模型,复现了该车曾经出现的各种晃车试验现象,从而验证了所建立模型的正确性。在此基础上,采用模态分析法对动力车晃车问题进行了机理研究,从而查找出引发晃车现象的主要因素。
1 试验研究
动力集中动车组在进行现场试验时,发现其中动力车在直线运行工况下140 km/h及以上速度时会出现晃车现象,图1给出了动力车直线工况晃车时的动力学响应波形图。从图中可以看出,车体前端、后端横向振动加速度信号都存在明显的周期性波动,振动频率约为1.1 Hz,振幅最大值接近1.0 m/s2;与此同时,车体晃动还带动轮对产生轻微晃动,使得轮轨横向力出现了相同频率的小幅波动。研究发现,虽然动力车晃车问题对其运行安全性影响较小,但是对车体横向平稳性指标具有较大影响,导致其最大值已经接近合格限度值。
针对动力车直线运行工况晃车问题,曾先后开展了多次专项试验,检测了不同结构参数和车轮踏面状态下的动力学响应数据。研究中系统梳理了历次试验数据,通过深入对比分析来探寻规律,查找影响因素。
1.1 结构参数调整
专项试验过程中对动力车部分悬挂参数进行了调整,包括:轴箱拉杆关节刚度由40 kN/mm减小为18 kN/mm;抗蛇行减振器关节刚度由50 kN/mm减小为25 kN/mm,车轮踏面外形保持不变。图2给出了结构参数改变前后测得的车体横向振动加速度对比波形图,图3给出了相应的车体横向平稳性指标对比散点图。可以看出,改变结构参数后,虽然车体横向振动加速度幅值有所减小,但是1.1Hz的周期性波动依然存在;车体横向平稳性指标有所减小,但最大值仍处于较大水平。这说明晃车问题并未通过轴箱拉杆关节刚度、抗蛇行减振器关节刚度的调整而彻底解决。

图1 动力车直线工况晃车波形图

图2 调整结构参数前后车体横向振动加速度实测波形图

图3 调整结构参数前后车体横向平稳性指标对比散点图
1.2 车轮踏面状态影响
保持动力车原有结构参数不变,使用如图4所示的磨耗后JM3踏面进行动力学试验。由于踏面出现凹磨,轮轨等效锥度由新轮时的0.06增大至磨耗后的0.30。图5给出了在磨耗车轮踏面下实测动力学响应波形图,图6给出了新轮与磨耗车轮踏面下车体横向平稳性指标的对比散点图。综合对比可知:在采用磨耗车轮后,动力车车体横向振动加速度周期性波动消失,晃车现象基本消除,车体横向平稳性指标明显减小,其最大值减小至2.50左右。
在进行对比分析的两次试验中,试验线路、运行速度等试验条件相同,动力车悬挂参数也相同,只有车轮踏面磨耗情况不同,也即在车轮磨耗后,动力车晃车现象有显著改善。因此可以初步判断动力车晃车现象属于低等效锥度下的车体蛇行失稳性质。

图4 JM3新轮和磨耗车轮踏面外形对比图
1.3 抗蛇行减振器安装角度影响
恢复车轮踏面的JM3新轮状态,将动力车抗蛇行减振器安装角度由原来的11°减小为4°,再次进行动力学试验。图7给出了抗蛇行减振器安装角度4°时实测动力学响应波形图,图8给出了不同抗蛇行减振器安装角度时的车体横向平稳性指标对比散点图。可以看出,减小抗蛇行减振器安装角度后,动力车晃车现象得到明显改善,车体横向振动加速度仅在个别区段出现小幅周期性波动,车体横向平稳性指标明显减小,其最大值约为2.20。这说明动力车直线运行工况晃车现象与抗蛇行减振器安装角度存在明显关联性。

图5 磨耗车轮踏面下动力车动力学响应实测波形图
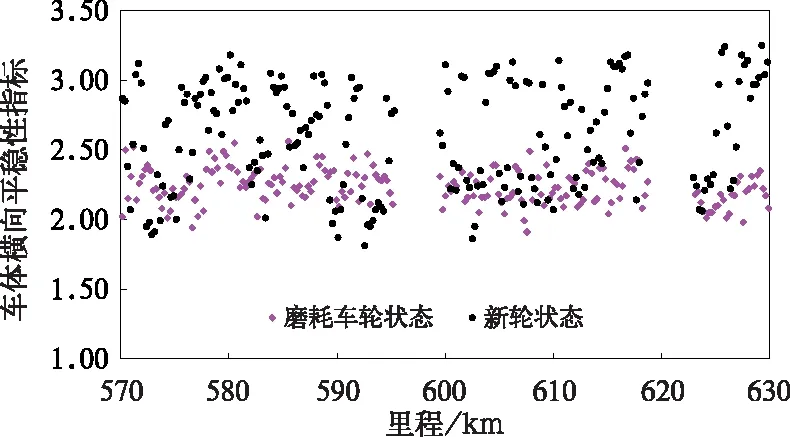
图6 新轮和磨耗车轮踏面下车体横向平稳性指标对比散点图
通过试验数据综合分析可以看出,动力车直线运行晃车问题主要与轮轨等效锥度和抗蛇行减振器安装角度有直接关系,在大的抗蛇行减振器安装角度和小的轮轨等效锥度条件下,会出现车体蛇行失稳现象。
2 仿真计算分析
为了深入分析动力车晃车现象产生的原因、作用机理以及改进措施,借助于动力学仿真计算软件进行了分析。将动力车假设为复杂的多刚体、多自由度系统,整个系统主要由车体、构架、轮对、驱动单元、空心轴、轴箱等质量以及弹簧、减振器等元件组成,整个模型共计90个自由端,如图9所示。模型中钢轨采用国内客专线路的60N廓形(与试验线路钢轨廓形相同)。
图10给出了原车初始结构状态下试验和仿真所得车体横向振动加速度对比波形图,可以看出计算所得车体横向振动加速度最大值约为1 m/s2,频率约为1 Hz,幅值和频率均与试验数据相一致。
图11和图12分别给出了采用JM3新轮(小等效锥度)和磨耗车轮(大等效锥度)时计算所得车体横向振动加速度对比波形图和频谱图。当采用小等效锥度车轮踏面时,车体横向加速度存在明显的周期性波动,振动频率均为1.1 Hz左右。而当采用大等效锥度车轮踏面时,车体横向振动加速度不存在1.1 Hz周期性波动,晃车现象消失。与前述动力车实际试验现象相符。另外,采用该模型进一步计算了抗蛇行减振器安装角度为11°和4°时的情况,同样复现了实际试验现象,抗蛇行减振器角度减小为4°后计算所得车体横向振动加速度不存在周期性波动,与试验现象相符。由于篇幅所限,这里不作介绍。

图7 抗蛇行减振器安装角度4°时动力学响应实测波形图

图8 不同抗蛇行减振器安装角度时车体横向平稳性指标对比散点图
图9 动力学分析模型
通过以上的试验现象复现,充分验证了所建立的动力学仿真计算模型的正确性。同时也进一步说明了动力车晃车问题与轮轨等效锥度和抗蛇行减振器安装角度具有明显的关联性。
3 作用机理分析
分析结果表明,动力车晃车问题主要与轮轨等效锥度和抗蛇行减振器安装角度具有明显关联性,该问题属于低等效锥度下的车体蛇行失稳性质。机车车辆出现车体低频横向晃动现象时均与系统模态特征的异常变化相关,因此需要通过动力车系统模态分析来研究其产生原因和作用机理。系统每一阶模态都会有模态频率和模态阻尼比,模态阻尼比主要表征对应模态的稳定性,模态阻尼比数值越大说明对应模态收敛性越好,越不易出现晃车。相反模态阻尼比小于0或接近0时说明对应的模态已经发散失稳或收敛很慢,很容易引起晃车。

图10 动力车车体横向加速度计算波形图-仿真与试验
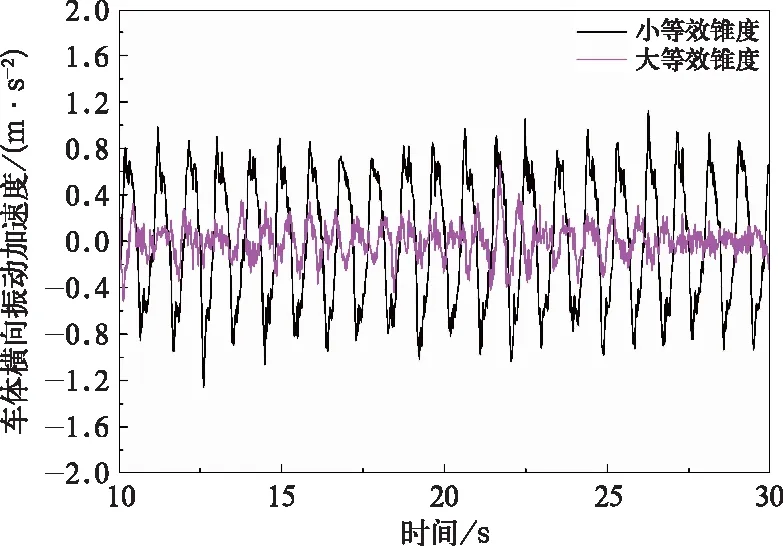
图11 不同轮轨等效锥度下计算所得车体横向振动加速度波形图

图12 不同轮轨等效锥度下计算所得车体横向振动加速度频谱图
3.1 车体模态随等效锥度变化
动力车车体存在点头、沉浮、横移、侧滚和摇头等模态,其中横移和侧滚模态耦合为上心滚摆运动和下心滚摆运动。除此以外,车体还存在由前、后转向架引起的两阶蛇行运动模态,这里对其做出如下定义:由后转向架引起的蛇行运动称为车体一阶蛇行模态,由前转向架引起的蛇行运动称为车体二阶蛇行模态。
图13和图14分别给出了不同轮轨等效锥度下车体模态的频率和阻尼比曲线。从图13中可以明显看出,除车体二阶蛇行模态外,其他运动模态的阻尼比均大于0.40,处于较大水平,说明这些模态的振型在不同轮轨等效锥度下均能够较好地收敛。而车体二阶蛇行的模态阻尼比在轮轨等效锥度很小时为负值,随着轮轨等效锥度的增大会逐渐增大,这表明该模态在轮轨等效锥度较小时会出现发散失稳或收敛很慢的现象,此时该模态的固有频率约在0.8~1.2 Hz范围内,这与试验中动力车出现晃车时的车体横向振动加速度主频相吻合。由此可判断动力车的晃车问题是由该动力车存在阻尼比较低的车体二阶蛇行模态所引发的。
通过计算分析可知,随着轮轨等效锥度的增大,动力车的车体二阶蛇行模态阻尼比逐渐增大,晃车现象逐渐消弱,相应地车体横向平稳性逐渐提高。这说明随着车轮踏面磨耗的产生发展,动力车晃车现象会趋于好转,甚至消失。

图13 车体模态频率随轮轨等效锥度变化曲线图

图14 车体模态阻尼比随轮轨等效锥度变化曲线图
另外,目前我国铁路线路的钢轨主要存在60N轨(客专线路)和60轨(普速线路)两种廓形,如图15所示。60轨廓形与标准JM3踏面匹配时的计算等效锥度约为0.10,大于60N轨廓形与标准JM3踏面匹配时的0.06。因此该动力车在客专线路上直线运行晃车现象与普速线路相比会更加明显。
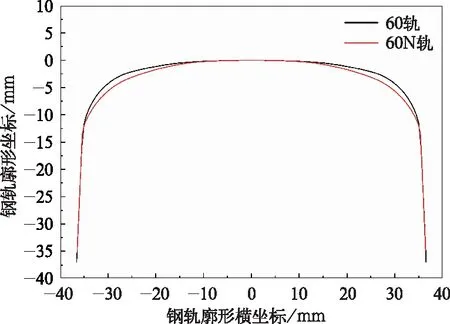
图15 60轨和60N轨廓形对比图
3.2 车体模态随抗蛇行减振器角度变化
图16和图17分别给出了不同抗蛇行减振器安装角度下车体各阶模态的频率和阻尼比变化趋势曲线。从图16中可以看出,除车体二阶蛇行模态外,其他模态的阻尼比均大于0.40,处于较大水平。而车体二阶蛇行模态的阻尼比随着安装角度的增大而逐渐减小,在安装角度达到11°时,其值已经减小为负值。这说明该模态在安装角度较大时会出现发散失稳或收敛很慢的现象,易引起晃车。且车体二阶蛇行模态频率随着安装角度的增大基本都保持在1 Hz左右,与试验中动力车晃车时车体横向振动加速度主频相吻合。

图16 动力车车体振动频率随抗蛇行减振器安装角度变化曲线图

图17 动力车车体模态阻尼比随抗蛇行减振器安装角度变化曲线图
3.3 作用机理
通过以上3个小节的分析可以确定,试验中出现的动力车晃车现象是由该车存在阻尼比较小的车体二阶蛇行模态所导致,而该模态的产生与抗蛇行减振器的安装角度有直接关系,本节通过受力分析来对其作用机理进行分析。
动力车抗蛇行减振器采用了左右对称但非平行布置的安装方式,图18给出了前转向架顺时针摇头运动时系统的受力分析图。当转向架具有顺时针摇头角速度时,车体前端左侧抗蛇行减振器受拉力为F1,它在横向和纵向的分力分别为F1x和F1y;右侧抗蛇行减振器受压力为Fr,它在横向和纵向的分力分别为Frx和Fry。从图中可以看出,左右抗蛇行减振器的纵向分力F1x和Frx数值相等,方向相反,可以相互抵消,而左右抗蛇行减振器的横向分力F1y和Fry数值相等且方向相同,其合力为FH。因此,由于抗蛇行减振器的这种左右对称但非平行布置方式,只要车体和构架间产生相对摇头或横移运动,都会在它们之间产生额外的横向作用力,该作用力会激发起车体的蛇行运动。这一分析与参考文献[3]中的论述相类似。
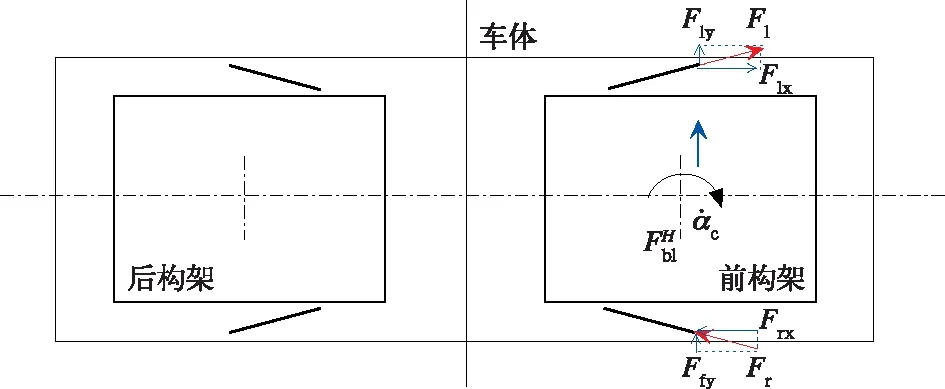
图18 车体摇头时受力分析图
4 结 论
采用实车试验和仿真分析相结合手段对动力车直线运行工况晃车问题开展了研究工作。通过试验数据综合分析明确了晃车问题主要与轮轨等效锥度、抗蛇行减振器安装角度有直接关联性。采用动力学仿真计算准确复现了动力车在历次试验中出现的晃车现象,对其产生原因和作用机理进行了研究。主要得出以下几点结论:
(1)动力车历次试验中晃车现象的复现充分说明了文中所建立动力学分析模型的正确性,证明能够采用该模型开展后续机理分析工作。
(2)动力车模态分析发现,引起车体晃车的主要是车体二阶蛇行模态,其主要作用机理为抗蛇行减振器安装角度设置不当,引起了动力车在低轮轨等效锥度下的车体二阶蛇行模态失稳。
(3)随着车轮踏面磨耗的发展,轮轨等效锥度逐渐增大,该动力车直线运行晃车现象反而会趋于改善。并且与普速线路(60轨)相比,动力车直线运行晃车现象在客专线路(60N轨)上更为明显。
虽然通过系统模态分析方法阐明了动力车直线工况晃车问题的产生原因和作用机理,但是尚未经过实际现场试验来检验,后续还需要开展相关试验验证工作。
