不同车轮踏面与高速60N钢轨道岔静态接触特性研究

闫正，陈嘉胤，徐井芒，王平，陈嵘，秦艳

(1.西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031；2.中铁上海设计院集团有限公司，上海，200070)

日益增长的庞大客运量对铁路运输系统的方方面面提出了严格的要求，轮轨接触关系控制着列车运行的姿态，是研究与解决轮轨磨耗、接触应力等问题的基础，是行车安全与稳定的重要保障。近年来，越来越多的人开始关注轮轨接触关系，并对此进行了大量的研究工作。钱瑶等[1-4]根据迹线法以及三维非赫兹滚动接触理论分别计算了不同车轮踏面和不同钢轨廓形相互接触时的各项参数，以此来对比其匹配性能。成棣等[5]运用改进层次分析法和判断矩阵权重分析对LMA 和S1002CN 踏面与60N 和60D 钢轨的匹配性能进行评价，认为S1002CN 踏面与60N 钢轨的接触状态优于CHN60钢轨，而该踏面匹配稳定性比LMA踏面的匹配稳定性差。邢璐璐等[6]针对LM，LMA和S1002CN等6种踏面与CHN60，60D和60N这3种钢轨进行了轮轨匹配的接触几何关系研究。POLACH等[7]阐述了采用新的非线性参数来评价轮轨匹配性能的研究进展，发现随运营里程增加，车轮等效锥度增大，非线性参数减小，而该现象与磨耗有关。杨光等[8]结合迹线法，采用BP 神经网络提出了一种快速计算轮轨接触点的方法，以实现轮轨接触几何分析计算的高效与准确。杨新文等[9]采用有限元方法，计算了轮轨间非赫兹接触时的影响系数，并对Kalker 的赫兹接触理论进行了优化处理。倪平涛等[10]结合迹线法与轨廓分区法来计算最小轮轨间隙，寻找轮轨真实接触状态。目前，针对轮轨接触关系的研究计算大多位于区间线路上。而作为轨道3 大薄弱环节之一的道岔，其轮轨接触关系更加复杂，对列车高速且平稳过岔更加重要。同时，区间线路60N 钢轨与道岔区60 钢轨由于廓形不一致，需在入岔及出岔部分设置钢轨过渡段以防止车轮在断面交接处产生冲击，这增大了钢轨生产建设难度及成本，故60N 钢轨在道岔区的应用意义尤为重大。对此，本文作者采用MATLAB 软件编写迹线法程序[11]以及基于Kalker 非赫兹滚动接触理论的CONTACT 软件[12]，分别计算LMA，S1002CN和XP55这3种车轮踏面与60N 钢轨道岔转辙器区某一断面的静态接触几何与静态接触力学参数，同时探讨不同轨道参数对轮轨接触几何的影响，并对其匹配性能进行分析，从而为轮轨接触关系的改进与优化提供参考。

1 静态接触几何参数

轮轨接触几何参数是轮轨接触关系最本质的反映。本文首先根据二维迹线法来计算轮轨接触点，以此来获得轮轨接触点对分布、蠕滑率、侧滚角和侧滚角系数、等效锥度、轮径差。二维迹线法是不考虑轮对摇头角，在二维平面内，通过横移量和侧滚角来确定轮轨接触点坐标。在计算过程中，钢轨轨距取为1 435 mm，轨底坡按照1∶40 设置，轮背内侧距取为1 353 mm，名义滚动圆半径取为460 mm。

1.1 车轮踏面

LMA，S1002CN 和XP55 这3 种车轮踏面的形状曲线如图1所示。

图1 3种车轮踏面形状曲线Fig.1 Shape curves of three types of wheel treads

这3种车轮被广泛应用于不同时速标准或型号的CRH系列高铁动车组列车轮对上。LMA踏面根据我国自主研制的LM踏面改进而来，增加了轮缘高度和轮缘处2 段圆弧的半径，使其更加圆润；S1002CN 踏面的前身是欧洲铁路联盟研制设计的S1002 踏面；而XP55 踏面则由法国研制，并应用于CRH5等型号的高铁列车轮对上。

1.2 钢轨廓形

由于60N 钢轨道岔转辙器区35 mm 顶宽的曲尖轨断面位于轮载过渡段，轮轨接触关系复杂，对不同车轮接触状态产生影响较大，对于研究岔区轮轨匹配性能具有代表性，故采用该断面进行计算分析，如图2所示。由图2可见：60N 钢轨基本轨从轨顶中央向轨距角方向依次由半径为200，60，16和8 mm的圆弧组成。在该断面中，曲尖轨顶宽为35 mm，降低值为1.3 mm，曲尖轨顶部打磨为半径3 mm的圆弧，以接近实际磨耗后的钢轨廓形。

1.3 轮轨接触点

在不同横移量下，3种车轮的轮轨接触点的分布如图3所示。由图3可知：当横移量为-12～-2 mm时，3种踏面的接触点均在尖轨顶端左右；当横移量为-2～12 mm时，LMA踏面接触点转移至基本轨上，S1002CN踏面接触点在2 mm处由尖轨顶端左右缓慢向轨距角方向移动，而XP55踏面接触点依然保持不变；当横移量在10 mm左右时，3种踏面均发生轮缘接触，接触点在轨距角左右；当列车侧逆向过岔时，受偏载力的影响，轮对一般趋向外侧横移，即横移量为正(>0)。故在踏面接触范围内，LMA 踏面与基本轨接触，而S1002CN 和XP55踏面则完成了轮载过渡。

图2 60N钢轨道岔断面Fig.2 Rail profile of 60N turnout

图3 轮轨接触点位置随轮对横移量的分布Fig.3 Distributions of location of wheel-rail contact points with wheelset lateral displacement

轮轨接触点对分布如图4所示，由图4可见：在踏面接触范围内，LMA 踏面接触点在基本轨顶部左右，分布较为均匀。S1002CN和XP55踏面接触点均在尖轨顶端左右，点对呈扇形状；随轮缘向尖轨工作边靠近，S1002CN 踏面接触点相对轮缘反向移动，分布逐渐均匀，轮轨接触状态逐渐变好；XP55 踏面则始终集中在尖轨顶端处，尽管接触点间的连续不间断分布使采用该踏面的列车行车平稳性较好，但可能导致轮轨接触应力过高，磨耗较大；另外，LMA 踏面的轮载过渡滞后于另外2 种踏面，延长了基本轨承受车轮荷载的作用，减少尖轨因接触应力过大而产生疲劳损伤的情况。

图4 轮轨接触点对分布Fig.4 Distributions of pairs of wheel-rail points

1.4 蠕滑率

蠕滑率反映了轮轨接触时的磨耗程度。在二维平面静态接触几何中，由于轮对摇头角、摇头角速度、侧滚角速度、轮对横移速度这几项参数均取为0，故纵向蠕滑率及自旋蠕滑率的计算公式如下[13]：

式中：i为1和2时分别表示左、右侧车轮；ξi1和ξi3分别为纵向和自旋蠕滑率；ri为车轮滚动圆半径；r0为车轮名义滚动圆半径；δi为轮轨接触角。

通过式(1)计算得到的3种车轮踏面的蠕滑率随横移量的分布如图5所示。

图5 蠕滑率随轮对横移量的分布Fig.5 Distributions of creepage with wheelset lateral displacement

由图5(a)可知：3 种踏面的左侧车轮纵向蠕滑率基本相同，且随横移量增大缓慢增大；对右侧车轮而言，在踏面接触范围内，随横移量增大，LMA 踏面的纵向蠕滑率绝对值逐渐减小，S1002CN 和XP55 踏面纵向蠕滑率绝对值逐渐增大；当横移量为0～6 mm 时，LMA 踏面纵向蠕滑率绝对值最大，磨耗较高，S1002CN 的次之，XP55 的最小；当横移量为6～9 mm 时，LMA 踏面纵向蠕滑率绝对值最小，S1002CN 的最大，相应磨耗较大，XP55 的居中；当轮缘接触时，3 种车轮踏面的纵向蠕滑率绝对值均陡增，其中S1002CN 的纵向蠕滑率绝对值最大，由此加剧轮轨间的侧磨；LMA 的纵向蠕滑率绝对值比S1002CN的小，XP55的最小。

由图5(b)可知：3 种踏面左侧车轮自旋蠕滑率随横移量增大略微减小，其中XP55踏面的自旋蠕滑率最大，LMA 与S1002CN踏面的自旋蠕滑率基本相同；对于右侧车轮而言，在踏面接触时，随横移量增大，LMA 和S1002CN踏面自旋蠕滑率绝对值略微减小，而XP55的踏面自旋蠕滑率绝对值则逐渐增大；当横移量为0～2 mm 时，LMA 纵向蠕滑率绝对值比另外2种踏面的稍大；当横移量为2～9 mm 时，S1002CN 踏面自旋蠕滑率绝对值最大；在轮缘接触后，3种车轮踏面纵向蠕滑率绝对值均陡增，然后缓慢回落，其中，XP55 踏面蠕滑率绝对值最大，由此引发的侧磨较高。S1002CN的踏面蠕滑率绝对值最小。

综合来看，LMA踏面在0 mm左右的蠕滑率较大，但随横移量增大适当减小，磨耗降低；S1002CN 踏面的蠕滑率绝对值逐渐增大，导致磨耗增加；当轮对横移量为8 mm 及以下时XP55 踏面蠕滑率基本不变。

1.5 等效锥度

等效锥度是指在某一横移量下，非锥形踏面如磨耗型踏面等效于1个锥形踏面[14]。等效锥度是衡量列车平稳性、振动响应等的重要指标。图6所示为采用简化法(即左、右车轮滚动圆半径差与2倍横移量的比值)计算得到的3种车轮踏面与该60N钢轨道岔断面接触时的等效锥度分布。

由图6可见：3 种车轮踏面的等效锥度随横移量的变化大致围绕坐标原点呈中心呈对称分布；当横移量为-2～2 mm 时，LMA 踏面等效锥度变化较大，其幅值为0.9 左右；S1002CN 踏面在1 mm左右等效锥度约为0.1；XP55踏面的等效锥度则无较大变化；当横移量为-8～-2 mm与2～8 mm时，3种车轮踏面的等效锥度基本保持不变，分布呈水平线状，其中S1002CN踏面等效锥度绝对值最大，LMA 的最小，但三者非常接近；当发生轮缘接触时，3 种车轮踏面的等效锥度绝对值均突增；当S1002CN 踏面在横移量分别达到-8 mm 和8 mm时，其等效锥度绝对值首先增大至1.2左右，然后缓慢下降至1.0左右；LMA踏面等效锥度的变化趋势与S1002CN的相似；而XP55踏面等效锥度绝对值持续增大，最后逐渐趋于稳定。

图6 等效锥度随轮对横移量的分布Fig.6 Distributions of equivalent conicity with wheelset lateral displacement

在踏面接触范围内，S1002CN 等效锥度绝对值最大，其所在轮对的曲线通过能力最强，有利于列车侧向过岔，但不利于列车的平稳运行。LMA踏面等效锥度绝对值最小，行车平稳性较好，但侧逆向过岔能力比S1002CN的弱。XP55的匹配性能则介于两者之间。

1.6 侧滚角与侧滚角系数

侧滚角是轮轴线与水平面的夹角，侧滚角系数则是侧滚角与2倍横移量的比值。当3种车轮踏面与该60N 钢轨道岔断面匹配时，其侧滚角与侧滚角系数随横移量的分布如图7所示。

由图7(a)可知：在踏面接触范围内，3 种车轮踏面的侧滚角绝对值基本相同，其中LMA 的值略微小于S1002CN，S1002CN的侧滚角则比XP55的略小，并在0 rad左右保持稳定，说明LMA踏面所在轮对姿态更接近水平；在轮缘接触范围内，3种车轮踏面侧滚角绝对值均陡增，并呈持续上升趋势；S1002CN 的值率先增大，其次是LMA 踏面，最后为XP55 踏面，3 种车轮踏面侧滚角绝对值在-12 mm 处依次达到13×10-3，12×10-3和10×10-3rad左右，在12 mm 处则依次达到10×10-3，9×10-3和5×10-3rad左右。

图7 侧滚角和侧滚角系数随轮对横移量的分布Fig.7 Distributions of roll angle and roll angle coefficient with wheelset lateral displacement

由图7(b)可知：由于侧滚角系数是通过侧滚角除以横移量得到，故除坐标原点左右外，其他横移量下侧滚角系数的变化规律与侧滚角的变化规律相似；当踏面接触时，LMA 踏面的侧滚角系数绝对值依然比S1002CN 和XP55 的侧滚角系数稍小；当轮缘接触时，3种车轮踏面的侧滚角系数绝对值陡增，其中S1002CN 侧滚角率先增大，最终在-12 mm和12 mm处分别稳定至6×10-4rad/mm和4×10-4rad/mm 左右；LMA 随后增大，侧滚角系数绝对值也在-12 mm 和12 mm 处分别稳定至5×10-4rad/mm和4×10-4rad/mm左右；XP55 踏面侧滚角系数绝对值呈逐渐增大趋势。

综合来看，LMA 踏面所在列车轮对，在踏面接触时的姿态能较好地保持水平，与该60N 钢轨道岔断面的匹配较好，S1002CN 与60N 钢轨道岔断面的匹配次之，XP55 与60N 钢轨道岔断面的匹配最差。

1.7 轮径差

轮径差将导致角速度相同的左、右车轮在钢轨上走行的距离存在差异，使轮轨间产生蠕滑。图8所示为3种车轮踏面轮径差随横移量的分布。

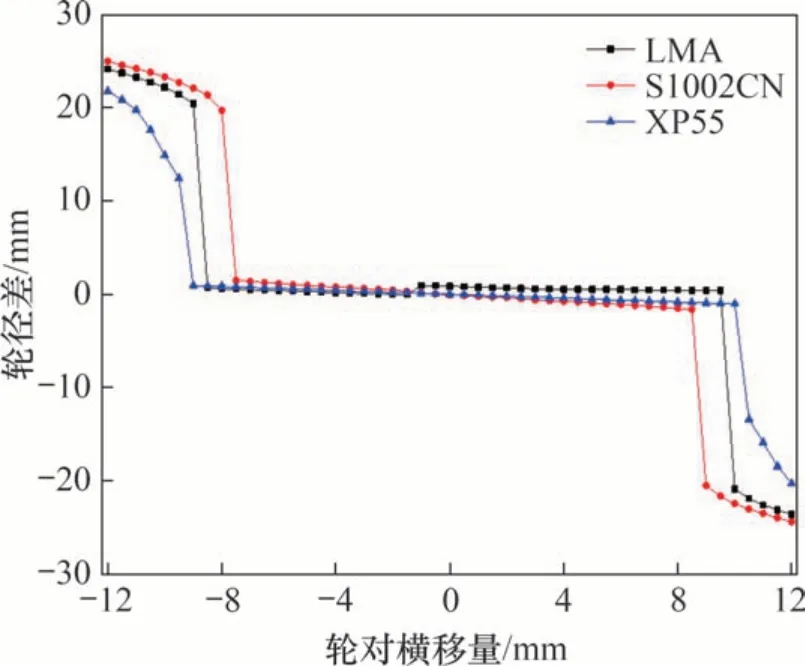
图8 轮径差随轮对横移量的分布Fig.8 Distributions of wheel radius with wheelset lateral displacement

由图8可见：当横移量为0～8 mm时，LMA踏面的轮径差最大，但随横移量增大有略微减小，S1002CN踏面的轮径差最小；当横移量为-8～0 mm时，情况恰好相反；当踏面接触时，3种车轮踏面的轮径差近似呈直线分布；当发生轮缘接触时，轮径差绝对值在-10 mm 和10 mm 左右突然增大，其中S1002CN踏面的轮径差绝对值最大，XP55踏面的最小。故在踏面接触范围内，LMA 踏面蠕滑效应明显，但随横移量增大LMA 踏面蠕滑效应有所降低；S1002CN踏面蠕滑效应较小；XP55踏面的蠕滑效应表现居中。

2 不同轨道参数对接触几何的影响

不同车轮踏面的轮轨匹配性能有所不同，而在不同轨道参数下，同一车轮的轮轨接触几何也存在差异。王文健等[15]计算了不同轨距和轨底坡下JM3磨耗型踏面与60N钢轨匹配时的接触几何参数以及蠕滑率。钱瑶等[16]针对LMA，S1002G 和XP55这3种车轮踏面与区间线路直线段60N钢轨，分别计算并分析了在1∶10，1∶20和1∶30轨底坡下的等效锥度、接触带宽等接触几何参数。陶功权等[17]基于轮轨接触几何关系以及轮轨非赫兹滚动接触理论，来评价地铁车辆常用的LM，S1002 和DIN5573这3种车轮踏面与60N钢轨在不同轨底坡下的匹配关系。本文主要分析轨距、轮背内侧距、轨底坡对轮轨接触点分布、侧滚角与侧滚角系数、等效锥度和轮径差的影响。

2.1 轨距

当窄轨距为1 432 mm、标准轨距为1 435 mm、宽轨距为1 440 mm时，3种车轮踏面与该钢轨断面匹配时的接触几何参数如图9所示。

由图9可见：对同一车轮踏面而言，随轨距增大，轮轨接触点位置发生变化时所需的横移量增大，轮缘接触情况发生所需横移量绝对值也增大，因此，其踏面接触范围变大，轮轨接触状态比窄轨距的好。无论轨距如何，LMA 踏面依然与基本轨有所接触，接触状态较好。S1002CN和XP55踏面仅与尖轨接触，但前者接触状态较好，后者在1 440 mm轨距下，接触点始终位于尖轨顶端左右，导致接触状态较差。

图9 轮轨接触几何参数随轮对横移量的分布Fig.9 Distributions of wheel-rail contact geometric parameters with wheelset lateral displacement

当横移量为-6～6 mm时，3种车轮踏面的侧滚角及侧滚角系数几乎无变化，表明轨距的增大或减小对踏面接触状态影响非常小。随轨距增大，3种车轮踏面的轮缘接触情况均延后发生，即轮缘接触出现时的横移量绝对值增大，表明随轨距增大，其轮对在侧逆向过岔时保持踏面接触状态的横移量范围更大，轮轨接触状态较好。

在踏面接触时，随轨距增大，3种车轮踏面的等效锥度绝对值均有略微减小，行车平稳性增强，但轮对的侧向过岔性能有所降低。同时，不同轨距对3种车轮踏面轮径差的影响很小。影响较大的区域主要发生在图像两侧的轮缘接触区域内，表现为轨距的增加使同一车轮踏面的轮径差绝对值幅值同样减小，蠕滑效应减弱。

2.2 轮背内侧距

轨距表征两侧钢轨轨距角处测量点之间的距离，轮背内侧距表征同一轮对下两侧车轮轮背间的距离，因此，轮背内侧距增大，可以认为是轨距的相对减小，故其对上述5项参数随横移量变化规律的影响与轨距随横移量变化规律基本相反。轮背内侧距取为1 350，1 353 和1 356 mm 时的轮轨接触几何参数随横移量的分布如图10所示。

图10 轮轨接触几何参数随轮对横移量的分布Fig.10 Distributions of wheel-rail contact geometric parameters with wheelset lateral displacement

由图10可见：当轮背内侧距增大时，3种车轮踏面接触点位置发生变化所需横移量减小，轮缘接触时的横移量绝对值也减小，故轮轨踏面接触范围缩小，接触状态逐渐变差。在同一轮背内侧距下，LMA 踏面仍然与基本轨有所接触，接触状态最好。S1002CN和XP55踏面虽然均只与尖轨顶端左右接触，但前者随横移量增大，接触点集中分布的现象逐渐减少，其静态接触的匹配性能也仍然比后者的好。

在踏面接触范围内，轮背内侧距的变化对侧滚角和侧滚角系数的影响较小，但在图像两侧陡增的部分较大，表现在随轮背内侧距增大，同一车轮轮缘接触发生时对应的横移量绝对值减小，其侧滚角和侧滚角系数有所增大。故较小的轮背内侧距有利于增大踏面接触范围，从而使轮轨接触状态变好。

随轮背内侧距增大，踏面接触时同一车轮踏面等效锥度绝对值略微增大。在轮缘接触时，同一车轮轮缘接触发生所需横移量绝对值减小，等效锥度绝对值幅值增大。轮径差在踏面接触范围内基本不随轮背内侧距的改变而变化，但在轮缘接触时变化范围较大。

2.3 轨底坡

图11和图12分别所示为各项轮轨接触几何参数在无轨底坡、1:40轨底坡和1:20轨底坡下随横移量的分布情况。

从图11和图12可知：随轨底坡增大(按无轨底坡、轨底坡1∶40、轨底坡1∶20顺序变化)，LMA和S1002CN 踏面的接触点位置变化明显；LMA 踏面轮缘接触发生位置基本没有改变，但其踏面接触时接触点位置发生改变所需横移量增大；S1002 CN踏面在基本轨上的接触点消失；XP55踏面则基本没有改变。对于前两者而言，轨底坡增大使车轮与基本轨接触的横移量范围减小，接触状态变差；XP55 踏面几乎不受轨底坡变化的影响，接触状态始终较差。

在踏面接触时，侧滚角与侧滚角系数略微减小。在轮缘接触时，随轨底坡增大，同一车轮侧滚角与侧滚角系数绝对值均有略微减小，但轮缘接触发生的位置基本保持不变。轨底坡增大有利于轮对趋于水平姿态，提高轮轨匹配性能。

轨底坡的变化在踏面接触时对等效锥度影响较大，在轮缘接触时影响较小。在踏面接触时，同一车轮在不同轨底坡下，其等效锥度绝对值明显减小，故侧向过岔性能有所下降，但行车平稳性得到提高。对于轮径差而言，除横移量-12～-8 mm 的范围外，轨底坡的改变无论是对踏面接触还是轮缘接触情况的影响均非常小，表现在不同轨底坡下同一车轮的轮径差值几乎没有改变，轮缘接触发生时的位置也基本没有改变。

图11 轮轨接触点位置随轮对横移量的分布Fig.11 Distributions of location of wheel-rail contact points with wheelset lateral displacement

图12 其他轮轨接触几何参数随轮对横移量的分布Fig.12 Distributions of other wheel-rail contact geometric parameters with wheelset lateral displacement

3 静态接触力学参数

通过Kalker 非赫兹滚动接触CONTACT 软件，计算在横移量为正的情况下，当3种车轮踏面与该60N钢轨道岔断面匹配时，不同横移量下的接触斑及法向接触应力分布，依次分析其匹配性能。3种车轮踏面匹配时非等比例的接触斑分布如图13所示，LMA 和S1002CN踏面对应横移量下的非等比例第二接触斑放大图如图14所示。与二维迹线法的轮轨纯刚性假设和单点接触不同，车轮与钢轨之间的接触具有弹性，因此，当LMA 和S1002CN踏面匹配时，均有基本轨、尖轨同时接触的情况发生。

赫兹接触基于弹性无限半空间、接触表面光滑、仅在接触范围内传递法向力这3项假设，是一种理想的接触状态[18]。而在实际的轮轨接触关系中，车轮与钢轨均为有限接触体，接触范围相对车轮踏面或钢轨断面尺寸并非无穷小，接触表面不再光滑，轮轨间除法向力外，还传递切向力，属于非赫兹接触。

由图13～14 可知：由于轮轨间产生非赫兹接触，接触斑均不是标准椭圆状。在踏面接触范围内，LMA 踏面的第一接触斑均位于该60N 钢轨道岔断面的基本轨上，随横移量增大，接触斑由近似椭圆状逐渐变为扁平状，单个接触斑内法向应力幅值所在位置逐渐向钢轨横坐标正方向移动。当横移量为0 mm 和1 mm 时，第二接触斑在尖轨顶端左右产生，其法向接触应力幅值分别为3 352 MPa 和2 262 MPa。S1002CN 和XP55 踏面的第一接触斑均在尖轨顶端左右。其中，对于S1002CN 踏面而言，第一接触斑随横移量增大，其形状逐渐接近椭圆，分布位置由尖轨顶端左右向尖轨轨距角左右缓慢移动，接触斑内亮色部分逐渐变淡，第二接触斑在横移量为2 mm 时产生，位于基本轨上，其法向应力幅值为3 795 MPa。XP55踏面接触斑则呈半椭圆状，其大小、位置、颜色分布及亮暗情况随横移量几乎没有改变。

由CONTACT 计算结果可知，3 种车轮踏面的第一接触斑分布与迹线法所计算得到的轮轨接触点分布一致。在踏面接触的情况下，外侧轮缘靠近尖轨工作边，横移量较大，故在不考虑第二接触斑的情况下，LMA踏面第一接触斑在基本轨上，而另外2种踏面的第一接触斑均在尖轨上，这表明S1002CN和XP55踏面均已与尖轨接触，由此可能加速尖轨产生的疲劳损伤。S1002CN 踏面随横移量增大，接触应力分布逐渐均匀，接触状态变好。XP55 踏面由于接触斑随横移量增大几乎不发生变化，使尖轨始终处于高应力状态，轮轨接触状态最差。而在轮缘接触时，S1002CN 踏面的接触斑内法向接触应力幅值分布面积比另外2 种踏面的小。而当横移量为0～12 mm 时，该踏面最大法向接触应力为7 267 MPa，比LMA 踏面的5 638 MPa和XP55 踏面的5 579 MPa 大。总体而言，LMA 踏面静态接触时的匹配性能最佳，S1002CN 踏面静态接触时的匹配性能其次，而XP55踏面接触状态有待改善。

图13 接触斑分布随轮对横移量的分布Fig.13 Distributions of contact patches with wheelset lateral displacement

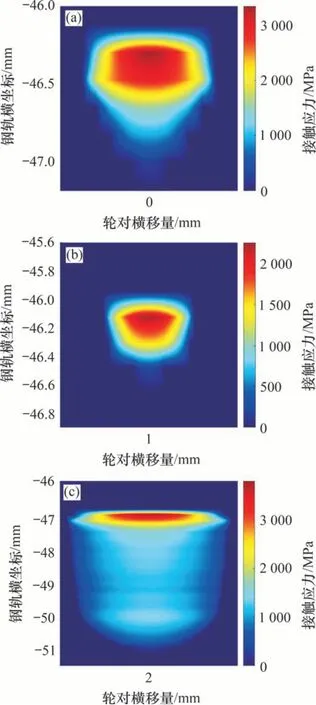
图14 第二接触斑放大图Fig.14 Amplification diagrams of the second contact patches

4 结论

1)LMA 踏面延长了基本轨的承载效应，有利于延缓尖轨的疲劳伤损。S1002CN 踏面接触点分布较为均匀，产生的轮轨磨耗较小；XP55 踏面轮轨接触始终处于高应力状态，接触状态较差。

2)在踏面接触下，LMA 踏面在0 mm 左右的蠕滑现象较明显，但随横移量增大，蠕滑率降低。S1002CN 踏面侧向过岔能力较强，但蠕滑率随横移量增大而增大，磨耗相应增加。XP55 踏面在8 mm及以下蠕滑率基本无变化。

3)在踏面接触范围内，增大轨距后，轮轨接触状态趋于良好，而侧滚角及侧滚角系数、轮径差几乎无变化，等效锥度绝对值略有降低。当增大轮背内侧距时，侧滚角及侧滚角系数、轮径差也基本无变化，但轮轨接触状态变差。在踏面接触时，轨底坡对等效锥度影响较大，对轮径差影响较小，而轨底坡增大导致侧滚角与侧滚角系数绝对值略微减小。

4)LMA 和S1002CN 踏面接触应力分布较均匀，后者随横移量增大，其单个接触斑内法向接触应力幅值逐渐降低，接触状态逐渐变好；在踏面接触时，XP55 踏面最大法向接触应力比另外2种踏面的大，其轮轨接触应力集中，接触状态不良。