无线传感器网络中的萤火虫时间同步改进模型

崔丽珍，曹 坚，安竹林，李丹阳，王巧利

1(内蒙古科技大学 信息工程学院，内蒙古 包头 014010) 2(中国科学院 计算技术研究所，北京 100190)

1 引 言

时间同步是无线传感器网络(Wireless Sensor Network，WSN)的一项支撑技术[1-3].对于WSN时间同步的研究，学者们提出了许多算法和协议[4-7]对该问题进行求解，当这些时间同步算法和协议被扩展到大规模网络时，存在距离时间基准节点跳距的增加，而发生同步过程中同步误差的累积，且大量的计算和复杂的数据包交换，使得WSN在实际运行中存在很大的负担.针对上述问题学者们开始利用自然界中的互同步现象来对WSN进行时间同步的研究[8].

萤火虫同步是一种互同步现象，互相临近的萤火虫通过脉冲形式的信号来相互传递信息，逐渐调整为同步闪烁的状态.萤火虫同步技术是解决WSN时间同步问题的一种新型同步机制[9]，基于萤火虫同步技术的脉冲耦合器时间同步模型很好的应用于WSN的时间同步中[10-13]，但大多算法模型忽略了负耦合强度在脉冲耦合同步过程中的作用.文献[14]在耦合延迟固定下的脉冲耦合振荡器系统的同步研究发现，只有负耦合才可能使系统取得同步.因此，本文提出了一种适用于WSN且具有抑制耦合的线性脉冲耦合振荡器时间同步模型.该模型避免了传统时间同步算法在多跳网络中同步误差积累的现象，并在无耦合时滞情况下，使用线性的状态函数更符合WSN使用廉价单片机作为处理器的节点计算能力.引入负耦合因子，通过激励与抑制相结合的相位耦合方式来缩短同步周期，提升全网络的同步速度.

2 同步模型以及相关定义

2.1 模型描述

将每个传感器节点看作为单个的脉冲振荡器，可以周期性输出脉冲信号作用在其它振荡器上，该模型具有线性的状态函数[15，16].对Peskin模型dx/dt=-λx+S0，令λ=0，S0=1/T，且t∈T〗，得到dx/dt=1/T，对此微分方程两边进行积分得x=t/T，T为周期，φ=t/T为相位变量，得到状态函数：

x=f(φ)=φ，φ∈1〗

(1)

用状态变量x描述振荡器，x在1〗上单调递增，当x到达阈值1时，振荡器激发，并且x立即跳回0，产生耦合强度ε，正耦合强度ε>0，负耦合强度-ε<0.由于状态和相位变量成线性关系，故使用φ统一表示.

在脉冲耦合振荡器系统中，激发后的节点瞬间下跳到0产生耦合强度，改变其他节点的相位，文献[17]证明了两个振荡器在同步演进中，由于相位差的减小，从而实现完全同步.文献[18]在脉冲耦合振荡器网络中实现了连续的相位演化，对脉冲耦合同步提供了严格的数学证明，分析了在相位连续性下达到同步的时间和同步收敛性.文献[19]研究了任意相位初始条件演化到全局的脉冲耦合振荡器同步方案.基于上述研究发现，在线性状态函数下，存在负耦合强度的抑制作用，使得未同步的节点下降到0点后，同样实现两个振荡器达到同步状态，并可以提升同步收敛速度.同步模型如图1所示，黑色圆圈表示振荡器i，白色圆圈表示振荡器j，分别处于不同的初始状态φi和φj.在该模型中，将振荡器的相位变量φ∈1〗以φ=1/2进行区间划分.随着同步演进过程中振荡器相位的变化，当某个振荡器的相位在φ=1瞬间下跳到φ=0时产生耦合强度ε，使其他振荡器的状态变量提升或者下降ε.通过耦合互异的方式构建出激励耦合与抑制耦合，提升同步速度，该模型的动态方程如式(2)所示.

(2)

图1 相位同步过程图

2.2 基本定义

定义1.基态GS(ground state)：

存在两个振荡器i和j，一个振荡器在某次激发之后相位为0，另一个振荡器的相位等于φ的状态.

相位φ区分在L1∈(0,1/2)和L2∈2,1)两个区间，基态的四种存在形式和两种表示方法如下：

GS1:φi,j=0,φj,i=φ,φ∈(0,1/2)

GS2:φj,i=0,φi,j=φ,φ∈2,1)

定义2.激发态fire(fire state)：

振荡器相位φ=1时的状态.

φi,j=φ,φj,i=1,φ∈(0,1)

定义3.同步状态Sync(Synchronization state)：

各个振荡器的状态和相位到达一致时的状态.

Sync:xi=xj=φi=φj=φ,φ∈1〗

3 两个振荡器同步

3.1 耦合方式

1)激励耦合Ex0(Excitatory couplings)

从初始状态GS1开始，在振荡器j激发后产生耦合强度ε，此刻振荡器i选择正耦合强度(ε>0)，使其相位提升一个增量Δφi.其状态表达式见式(3)：

φ=φi+Δφi=f-1(minφi)+ε,1〗)=F+(φi,ε)

(3)

当满足条件A：F+(φi,ε)≥1，系统达到同步.

2)抑制耦合In0(Inhibitory couplings)

从初始状态GS2开始，振荡器j激发后产生耦合强度ε，此时振荡器i选择负耦合强度(-ε<0)，振荡器i进行一耦即减的相位抑制作用，状态表达式定义见式(4)：

φ=φi+Δφi=f-1(0,maxφi)-ε〗)=F-(φi,ε)

(4)

当满足条件B：F-(φi,ε)≤0，系统达到同步.

3.2 同步过程

1)从GS1初始状态开始：

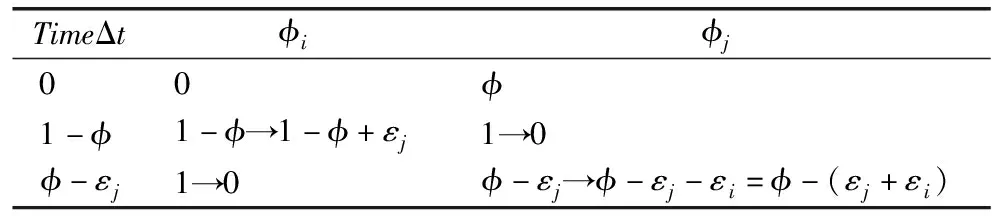
在振荡器j激发瞬间，振荡器i激励耦合同步.当εj≥φ时，振荡器i，j达到同步.否则同步演化的相位变化见表1.

表1 两个振荡器从GS1开始的相位变化表

Table 1 Phase changes of two oscillators starting fromGS1

TimeΔtϕiϕj00ϕ1-ϕ1-ϕ→1-ϕ+εj1→0ϕ-εj1→0ϕ-εj→ϕ-εj-εi=ϕ-(εj+εi)

2)从GS2初始状态开始：

在振荡器j激发瞬间，振荡器i抑制耦合，当φi=1-φ-εj≤0，振荡器i，j达到同步状态.否则同步演化的相位变化见表2.

3.3 同步条件分析

通过两个振荡器组成的振荡器系统在基态时的相位差来定义同步过程中的激发映射(firing map)与回归映射(return map)：

φi,j(tp,i)=φj(tp,i)-φi(tp,i)=φj(tp,i)-0=φp,i

(5)

其中p表示振荡器i的激发时刻.

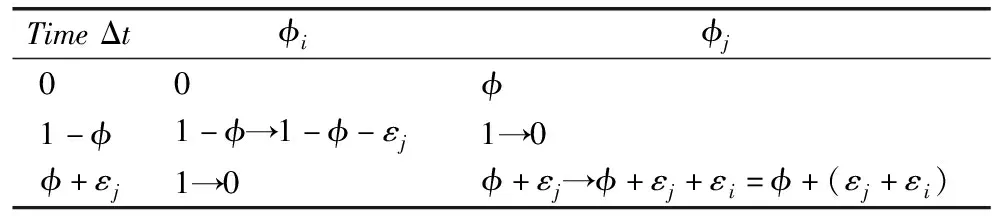
表2 两个振荡器从GS2开始的相位变化表

Table 2 Phase changes of two oscillators starting fromGS2

TimeΔtϕiϕj00ϕ1-ϕ1-ϕ→1-ϕ-εj1→0ϕ+εj1→0ϕ+εj→ϕ+εj+εi=ϕ+(εj+εi)

定义4.激发映射：从基态φi=0,φj=φ起，振荡器j第一次达到激发状态时振荡器i的相位.

h：φp,i→φq,j:φq,j=h(φp,i)

定义5.回归映射：从基态φi=0,φj=φ起，振荡器i第一次达到激发状态时振荡器j的相位.

R：φp,i→φp+1,i:φp+1,i=R(φp,i)

由表1,2分别得到两种初始状态的回归映射：

R(φp,i)=φ-(εj+εi)

(6)

R(φp,i)=φ+(εj+εi)

(7)

在i某次激发之后，j的相位比上次i激发时减少或增加了εj+εi.

通过分析R(φp,i)可以得到两个脉冲耦合振荡器到达同步的同步条件：

定理1.【两个脉冲振荡器同步条件】对于两个振荡器i和j，如果耦合强度满足式(8)：

εj+εi≠0

(8)

则它们达到同步状态.

证明：由于正耦合强度ε>0，负耦合强度-ε<0，且，故εj+εi>0恒成立，得到两种初始状态下的回归映射：

R(φp,i)=φ-(εj+εi)<φ

(9)

R(φp,i)=φ+(εj+εi)>φ

(10)

表明振荡器i和j的任意初始状态都会使两者的相位单调向着0或者1进行演化，两个脉冲耦合振荡器组成的振荡器系统达到同步状态.

通过上述分析，根据系统在两种不同的初始状态下的同步演进过程，构建出完整的状态转移图验证系统同步性.由图2所示，系统可从任意基态作为初始状态进行相位演化，到达激发态后选择合适的相位耦合方式，耦合强度的影响使得系统逐渐趋向于同步条件A或B，在有限状态机中的每个状态转化到最终的同步状态.

图2 两个振荡器同步有限状态自动机

4 多振荡器同步

4.1 耦合方式

分析多振荡器进行同步演化时，需要考虑多振荡器系统内其他振荡器处于激发瞬间的耦合强度Σk∈Eεk对同步进程的影响.其中E表示在振荡器i和振荡器j激发演化过程中到达激发状态振荡器的集合.

1)激励耦合Ex1(Excitatory couplings)

振荡器i和j在GS2初始状态下，若Σk∈Eεk使振荡器i和j的相位增加到φi=φj=1，振荡器i，j到达同步，组成振荡器同步组.

2)抑制耦合In1(Inhibitory couplings)

振荡器i和j在GS1状态下进行同步演化.Σk∈Eεk使振荡器i和j的相位下降到φj=φi=0，振荡器i，j到达同步，组成一个振荡器同步组.

4.2 同步过程

1)从基态GS1开始：

当φ≤Σk∈Eεk，则经过In1使得φi=φj=0，振荡器i和j同步，否则未达到同步.本文主要分析未同步状态，其相位变化见表3.

表3 多振荡器从GS1开始的相位变化

Table 3 Phase changes of multiple oscillators starting withGS1

TimeΔtϕiϕj00ϕ1-ϕ+Σk∈Eεk-Σk∈Eεk=1-ϕ1-ϕ→1-ϕ+εj1→0ϕ-εj-Σk∈Eεk1→0ϕ-εj-Σk∈Eεk→ϕ-εj-εi-Σk∈Eεk=ϕ-(εj+εi+Σk∈Eεk)

2)从基态GS2开始：

振荡器i和j受到Σk∈Eεk的激励作用，若Σk∈Eεk足够大使得φi=φj=1，则振荡器i和j同步.否则振荡器j需经过1-φ-Σk∈Eεk相位φj=1，振荡器j激发，此时φi=1-φ-Σk∈Eεk∈(0,1/2)，进行抑制耦合同步.当1-φ-Σk∈Eεk-εj≤0时，振荡器i和j到达同步.本文主要分析未到达同步的情况，其相位变化见表4.

4.3 同步条件

由表3和表4可知，多振荡器系统中振荡器i和j回归映射分别为：

R(φp,i)=φ-(εj+εi+Σk∈Eεk)

(11)

R(φp,i)=φ+(εj+εi+Σk∈Eεk)

(12)

通过式(11)、式(12)可以看出，在i某次激发之后，j的相位比上次i激发时减少或增加了εj+εi+Σk∈Eεk.因此，得到两个脉冲耦合振荡器的同步条件如式(13).

定理2.【多振荡器系统同步条件】对于一个由N个振荡器组成的的非漏电脉冲耦合振荡器系统，令E={ε1,ε2,…,εN}为系统中所有振荡器的耦合强度的集合，如果该系统满足条件(13)：

(13)

∀E1,E2⊂E，E1∩E2=Ø

则其能够到达同步.

证明：对于系统中的两个振荡器i和j或两个振荡器组m和n，令:

表4 多振荡器从GS2开始的相位变化

Table 4 Phase changes of multiple oscillators starting withGS2

TimeΔtϕiϕj00ϕ1-ϕ-Σk∈Eεk1-ϕ-Σk∈Eεk→1-ϕ-Σk∈Eεk-εj1→0ϕ+Σk∈Eεk+εj+Σk∈Eεk-Σk∈Eεk=ϕ+Σk∈Eεk+εj1→0ϕ+Σk∈Eεk+εj→ϕ+εj+εi+Σk∈Eεk=ϕ+(εj+εi+Σk∈Eεk)

εm，εn和Σk∈Eεk是多个耦合强度ε的累加，m和n为不同的振荡器组，其中的振荡器互不同步，且εj+εi+Σk∈Eεk>0，得到回归映射：

R(φp,i)=φ-(εj+εi+Σk∈Eεk)<φ

(14)

R(φp,i)=φ+(εj+εi+Σk∈Eεk)>φ

(15)

分析R(φp,i)得到振荡器i和j的任意初始状态都会使两者的相位单调向着0或者1进行演化，最终互相吸收成为一个振荡器组.

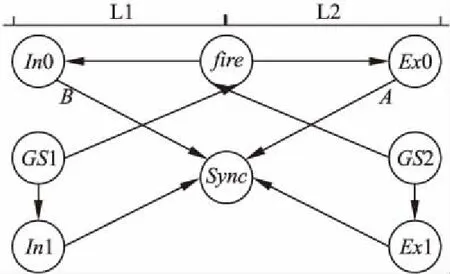
图3 多振荡器同步有限状态自动机

振荡器组的耦合强度为两个振荡器耦合强度之和，即εi,j=εj+εi.随着同步的演进，整个系统中会出现多个振荡器同步组，各个振荡器组再互相吸收，最后逐渐减少到两个较大的振荡器组，组成一个振荡器组时系统达到同步状态.多振荡器系统同步过程的状态转移由图3所示，在有限状态机中的每个状态转化到最终的同步状态.

5 仿真与验证

仿真环境使用Java语言在Eclipse下开发的脉冲耦合振荡器模型的仿真程序，对本文模型进行数值分析，并与适用于WSN的非漏电脉冲耦合振荡器同步模型[13]在相同仿真环境下进行实验对比.

5.1 耦合参数对同步周期的影响分析

将初始相位φ设置为T〗上的一个随机数，耦合强度ε设为_base-1/2*ε_base*ε_ratio,ε_base+1/2*ε_base*ε_ratio〗中一个随机数，其中ε_base为耦合强度基数值，ε_ratio为耦合强度数值比率.

图4为同步所需仿真周期随ε_ratio对系统进行了1000次同步仿真的变化情况，分别设定ε_base=0.05，ε_ratio=0.05和ε_ratio=0.2，通过两组差值较大的耦合强度数值比率分析其对系统同步的影响.从图4可以看出，当振荡器数目足够大的时候，仿真周期并不随其发生变化，同时两组数据的线性走势趋同，说明耦合强度的数值比率ε_ratio的大小对于振荡器系统的同步影响微小.由于耦合强度取决于ε_ratio和ε_base，因此将ε_ratio的值设定为0.1，分析与讨论ε_base和振荡器个数对同步周期的影响.

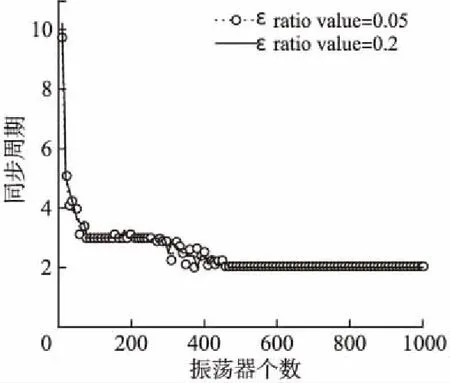
图4 不同ε_ratio的同步周期数随振荡器数目的变化情况(ε_ratio=0.05,0.2; ε_base=0.05)

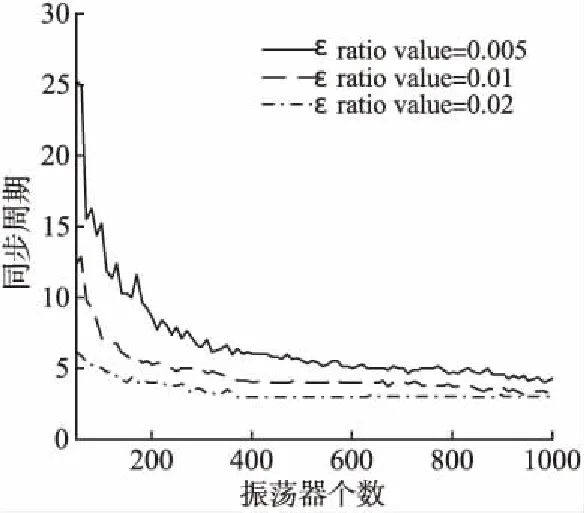
图5 不同ε_base的同步周期数随振荡器个数的变化情况(ε_base=0.005,0.01,0.02; ε_ratio=0.1)

通过对比三组不同的ε_base值，分析在振荡器个数从50扩展到1000所需要的仿真周期数随振荡器个数的增加时的变化情况.由图5所示，系统中的振荡器越多，振荡器越容易组合成为同步激发的振荡器组，仿真周期数随着振荡器个数的增加而非线性的减小.因此，ε_base成为系统耦合强度差异的主要参数，耦合强度越大，同步所需周期数就越少.

5.2 模型同步效果分析

设置振荡器数量为10(小规模)和50(较大规模)两种不同网络规模组成的实验场景，分析本文模型在不同数量振荡器的实验场景下的同步性能.如图6与图7所示，将该模型与非漏电脉冲耦合振荡器模型分别在振荡器数量为10和50的两种大小不同规模的实验场景中，进行100次的同步周期对比实验.

图6 两种模型在振荡器数目10时的同步周期(ε_base=0.005; ε_ratio=0.1)

如图6所示，本文模型到达同步所需的同步周期低于非漏电脉冲耦合振荡器模型的同步周期，表现出该模型较快的同步速度.如图7所示，该模型到达同步的所需的仿真周期的期望与方差小于非漏电脉冲耦合振荡器模型，表现出该模型的较强的稳定性和较好的同步性能.实验结果表明，在不同规模的振荡器模型中，本文模型具有较好的同步效果.

图7 两种模型在振荡器数目50时的同步周期(ε_base=0.005; ε_ratio=0.1)

从宏观的角度进行同步速度的对比观察，由图8所示，两种系统模型达到同步所需要的仿真周期数随振荡器数目从10逐渐增加到100的变化情况.同步速度随着振荡器数量的扩展而提升，且在同样数目的振荡器系统中，本文模型到达同步状态需要更少的同步周期，有效的提升了系统同步速度.

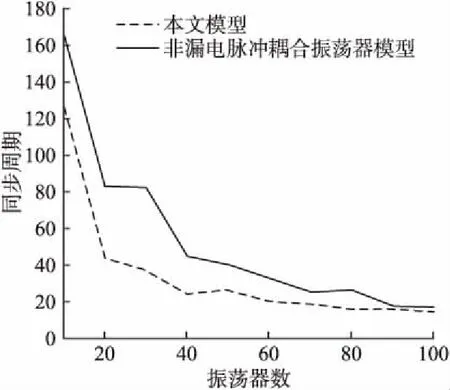
图8 两种模型同步所需仿真周期随振荡器数目的变化情况(ε_base=0.005; ε_ratio=0.1)

6 结束语

萤火虫同步技术是解决WSN时间同步问题的一种新型同步机制，本文在基于萤火虫同步算法提出了一种适用于WSN的时间同步改进模型.对两个振荡器以及多振荡器系统进行理论分析，包括状态函数、耦合方式、同步过程等，给出了振荡器系统的同步条件，证明了满足此条件的振荡器能够达到同步.通过仿真实验，验证了本文模型具有很好的稳定性的同时降低了同步周期，加快了WSN节点之间的同步速度.