基于非因果滤波和零点法的近断层脉冲型地震动识别方法

冯 俊， 赵伯明， 赵天次

(北京交通大学 土木建筑工程学院，北京 100044)

近几十年来，大量近断层地震动的资料得以采集，这些近断层地震动表现出明显不同于普通远场地震动的特征。由于断层破裂的滑冲效应和方向性效应[1-3]，近断层地震动速度时程通常表现出高速度幅值和明显的速度脉冲的特征。这种速度脉冲在很短的时间内将地震能量输入到结构中，极大增加了长周期结构破坏的可能性[4-9]。因此，脉冲型地震动的准确分类和定量识别对近断层区域结构的抗震设计有重要意义。

近断层地震动是地震危险性分析的重要组成部分，其定量表征和识别是地震工程研究者十分关心的内容。一些学者根据地震发生机制、震源和场地的位置关系判断是否存在方向性效应，从而对近断层地震动进行分类。一些学者从地震动速度时程中提取脉冲信号，并以脉冲信号的振幅和能量作为识别指标，定量识别脉冲型地震动记录。

在分析地震动速度时程时，其脉冲分量的充分提取是关键，识别结果的准确性取决于脉冲波形与初始地震动记录的拟合程度。Baker[10]基于连续小波变换提取主脉冲波形，并以主脉冲波形的振幅和能量作为地震动识别的量化依据。然而连续小波变换受到基函数的约束，仅通过尺度自适应得到的脉冲波形的匹配程度有限，导致该方法遗漏了许多非常明显的脉冲型地震动[11-12]。Zhai等[13]利用Dickinson等[14]数学模型拟合速度脉冲波形，并提出基于能量的脉冲型地震动识别方法。Zhao[15]基于三角函数的性质的速度零点法(zero velocity point method, ZVPM)提取脉冲波形，进而识别脉冲型地震动。但数学模型的自适应性较差，只能拟合高度对称的脉冲波形，不能有效识别非对称脉冲波形的地震动记录[16]。近年来，杨成等[17-20]提出基于经验模态分解(EMD)和集成经验模态分解(EEMD)的脉冲型地震动分析方法，但是EMD和EEMD分解信号时容易出现模态混淆，无法有效分解频率相近的信号分量，因此不能充分提取地震动记录中脉冲分量。

目前亟需一种实用、有效的方法来选择近断层脉冲型地震动记录。因为以往的脉冲型地震动记录的识别程序比较复杂，实际使用较困难，在分析新的地震动记录时，往往需要求助于程序的开发者。

本文提出了一种基于Butterworth非因果低通滤波器和零点法的脉冲型地震动分析方法。该方法流程简便，易于再现，提取的速度脉冲信号与初始地震动记录拟合效果较好。此外，以脉冲信号的能量占比和幅值比例作为量化指标，对单脉冲型地震动和双脉冲型地震动进行分类识别，并与既有常用的脉冲型地震动识别方法进行比较，验证了本文方法可靠性。

1 基于Butterworth滤波器和零点法提取脉冲

1.1 单脉冲信号提取

以正弦波说明零点法[21]的基本原理，如图1所示。两个连续的零点C1～C2，C2～C3之间的信号为半周期区间，而相邻的两个半周期信号可以视为一个周期区间。基于零点法的原理，通过一系列零点将地震动速度时程v(t)分割成许多半周期区间。选取峰值(PGV)所在的半周期区间为最显著半周期区间，叠加上与之相邻的峰值较大的半周期区间，可以得到完整循环振动的脉冲波形，如图2所示。

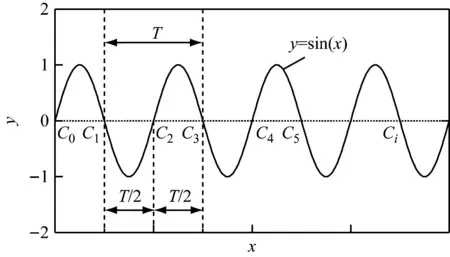
图1 基于正弦波解释零点法的原理Fig.1 Illustration of the zero-point method with a sinusoidal signal

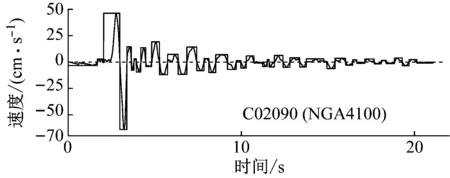
图2 基于零点法分析地震动速度时程Fig.2 Analysis of ground motion based on zero-point method

然而，基于零点法提取的脉冲振动区间包含许多涟波(周期或幅值都远小于脉冲分量的高频分量)，如图3所示。这些高频的涟波不仅影响脉冲型地震动的识别结果，还影响脉冲周期的计算结果，因此需要先过滤这些高频分量。

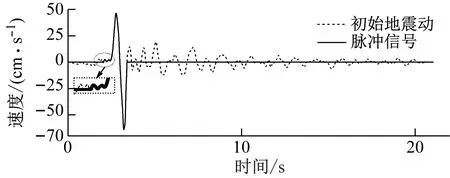
图3 基于零点法提取脉冲信号Fig.3 Pulse signal extraction based on zero-point method

Butterworth滤波器在不同滤波阶数下的地震动的参数稳定性较好，因此在地震工程中应用广泛[22]。滤波器根据因果性可进一步分为因果和非因果滤波。因果滤波会引起相位超前，即滤波后地震动信号的相位超前于初始地震动信号。非因果滤波在信号时域范围内分别向前和向后两个方向进行因果滤波，能消除单一方向因果滤波带来的相位失真[23]。Butterworth非因果滤波器的幅频特性HB(f)如式(1)所示

(1)

式中,f、fc、n分别为信号的频率、截止频率和滤波器阶数。

非因果滤波能实现零相位滤波，相较因果滤波更具优越性，因此本文采用4阶Butterwort非因果低通滤波器分析地震动速度时程。解耦过程的关键是确定截止频率(fc)，截止频率过低时可能出现低频脉冲分量“漏频”现象，导致脉冲特征不明显；截止频率过高时无法充分去除高频分量，影响脉冲参数的计算。

根据相关研究[24]，地震动速度时程中划分低频脉冲分量和高频分量的频率阈值在1～4 Hz，并且不同地震动记录存在不同的频率阈值。因此本文以4 Hz为初始截止频率，然后以0.01为公差递减，直到基于零点法提取的脉冲波形中不存在高频涟波为止。脉冲波形的极值点个数是用来判断是否存在涟波的重要依据，当提取的脉冲波形中只存在一个极大值和一个极小值时，则可以认为已经完全过滤掉高频涟波。基于Butterworth非因果低通滤波器和零点法提取的单脉冲信号v1p(t)如图4所示。

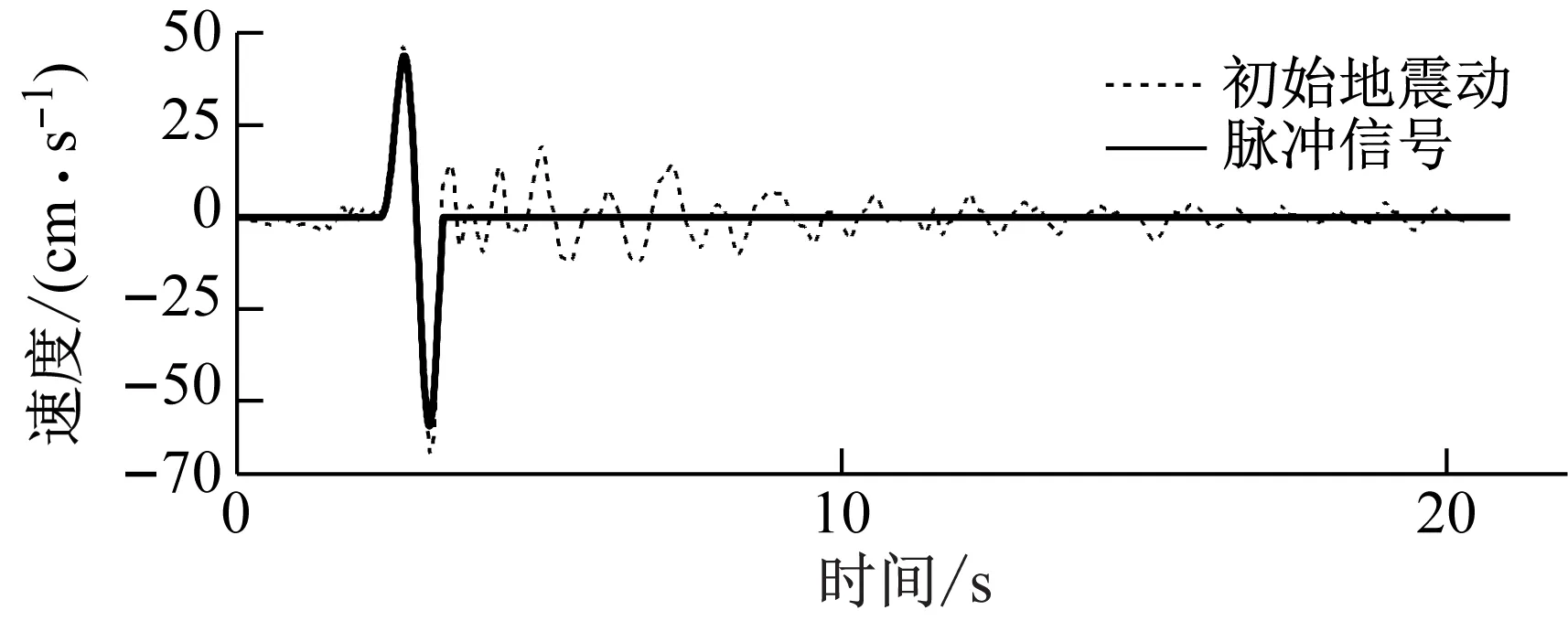
图4 基于零点法和Butterwort非因果低通滤波器 提取脉冲信号Fig.4 Pulse signal extraction based on zero-point method and Butterworth non-causal low-pass filter

1.2 双脉冲信号提取

在以往的脉冲型地震动识别方法[10-13]中，往往只考虑地震动速度时程中只存在单个显著速度脉冲波形的情况，当地震动记录中出现多个显著脉冲波形时，这些识别方法将失效。Zhai等[16]根据有效半周期区间的数目将地震动分为5类，但该方法无法确定地震动速度时程中的完整脉冲波形的个数，也无法获得其他重要的脉冲参数，如脉冲周期和脉冲峰值等。

Alavi等[5]认为近断层地震动的多脉冲特性会显著增加结构破坏的可能性。一些学者提出近断层多脉冲地震动与非方向性效应、断层类型、场地条件等因素相关[25-26]。此外，由于脉冲不仅有较大的幅值，还具有较大相对能量占比，地震动速度时程中一般不会超过2个显著的完整脉冲波形[12]。为了进一步识别速度时程中具有2个显著脉冲波形的近断层地震动记录，本文提出双脉冲信号提取方法。

(a) 初次脉冲信号

(b) 二次脉冲信号

(c) 双脉冲信号图5 双脉冲信号的提取Fig.5 Extraction of double-pulse signal

(2)

因此，基于Butterworth非因果低通滤波器和零点法的双脉冲信号提取流程如图6所示。

图6 双脉冲信号的提取流程Fig.6 Extraction procedure of double-pulse signal

从图6可知，主要分为以下几个步骤：① 以初始截止频率为4 Hz对初始地震动进行Butterworth非因果低通滤波；② 基于零点法的原理，提取PGV所在的半周期区间和与之相邻的峰值较大的半周期区间，作为一个完整的脉冲波形；③ 判断脉冲信号中是否存在高频涟波，以公差为0.01递减，直到提取的脉冲波形中只存在一个极大值和一个极小值；④ 重复前三个步骤，将对初次提取脉冲信号后的分量进行第二次脉冲提取，最后叠加初次脉冲信号和二次脉冲信号作为地震动的双脉冲信号。

2 脉冲型地震动的识别标准

为了确定近断层地震动的识别标准，需要建立一个包括单脉冲型地震动、双脉冲型地震动和非脉冲型地震动的综合数据库作为训练数据。根据Baker[10]对数据库的选择标准，本文从NGA-WEST2数据库中选择了矩震级Mw≥5.5且断层距Rrup≤30 km的地震动事件，得到936个地震动事件的2 808条记录。因为一些低振幅的记录难以通过视觉检查将其标记为脉冲型地震动或非脉冲型地震动，所以地震动速度时程的峰值PGV≥30 cm/s作为地震动记录选择的另一个标准[10-13]。根据以上约束建立一个包含666条地震动记录的数据库，并根据既有近断层地震动识别方法和视觉检查进行分析，将这666条地震动记录人为识别为242条非脉冲型地震动、364条单脉冲型地震动和60条双脉冲型地震动。本文建立的数据库中不同类型的近断层地震动数目充足，这是进一步提出地震动量化识别标准的重要依据。

脉冲型地震动中速度脉冲分量分担了相当多的一部分地震动能量，因此脉冲能量是脉冲型地震动识别的重要依据[13-19]。本文将相对脉冲能量指标Er定义为脉冲信号与初始地震动速度时程的能量比值，其表达式为

(3)

式中：ts、te分别为时间轴t上的脉冲信号起止点；vp(t)为速度脉冲信号；v(t)为初始地震动速度时程。

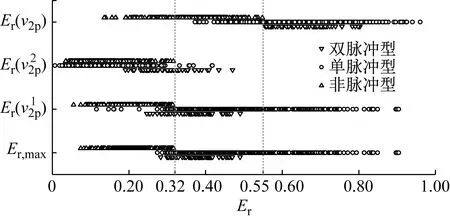
图7 近断层地震动的相对脉冲能量指标与分类结果的 分布关系Fig.7 Distribution of Er versus classification results of near-fault ground motions

2.1 单脉冲型地震动识别标准

为了量化识别脉冲型地震动，需要定义一个指标阈值，超过阈值就可以归类为脉冲型地震动。经过综合分析图7中单脉冲型地震动记录的识别结果与相对脉冲能量指标之间的关系，本文最大相对能量指标Er,max=0.32作为单脉冲型地震动识别的阈值。如果地震动速度时程中只有一个显著脉冲波形，单脉冲型地震动的判断标准如式(4)

Er,max>0.32

(4)

2.2 双脉冲型地震动识别标准

Er(v2p)>0.55

(5)

此外，双脉冲型地震动中的2个脉冲信号都应具有较大的相对能量比例，并且2个脉冲信号的相对脉冲能量指标和脉冲峰值都比较相近。为了避免双脉冲信号v2p(t)中两个脉冲信号的能量指标和脉冲峰值相差较大，双脉冲型地震动还应该满足下列条件

(6)

或

(7)

(8)

因此，双脉冲型地震动的识别标准为：满足式(5)和式(6)，或者满足式(5)、式(7)和式(8)。

3 地震动识别结果

基于本文的近断层脉冲型地震动识别标准，对上述666条近断层地震动进行识别，得到349条单脉冲型地震动和60条双脉冲型地震动。为了验证本文提出的脉冲型地震动识别方法的可靠性，将与Baker和Zhai的近断层识别方法进行比较。本文的地震动识别算法基于MATLAB软件编程实现，具体程序详见https://github.com/JUNFeng96/PulseClassification-NCLPF_ZPM。

3.1 与Baker的方法对比

Baker[10]利用连续小波变换提取脉冲信号，并基于脉冲能量和脉冲峰值的复合脉冲指标(PI)，对近断层地震动进行分类。对比Baker和本文的方法对666条地震动的分类结果，如图8所示。纵坐标为Baker的脉冲指标PI，Baker量化识别脉冲型地震动的标准为：当PI>0.85时，该记录为脉冲型地震动；当PI<0.15时，该记录为非脉冲型地震动；当PI介于0.15与0.85时该方法失效。横坐标为本文方法的识别结果，脉冲个数等于0为模糊区域，表示该记录不被本文识别为脉冲型地震动，脉冲个数等于1和2分别代表单脉冲型地震动和双脉冲型地震动。从图8可知，基于Baker和本文的分类结果划分为6个区域，并给出了各区域样本数目及占比。D区域中的样本被本文与Baker的方法都识别为脉冲型地震动记录，其中一部分记录被本文的方法进一步识别为双脉冲型地震动；而A和F区域为本文与Baker的识别结果冲突的地震动记录。

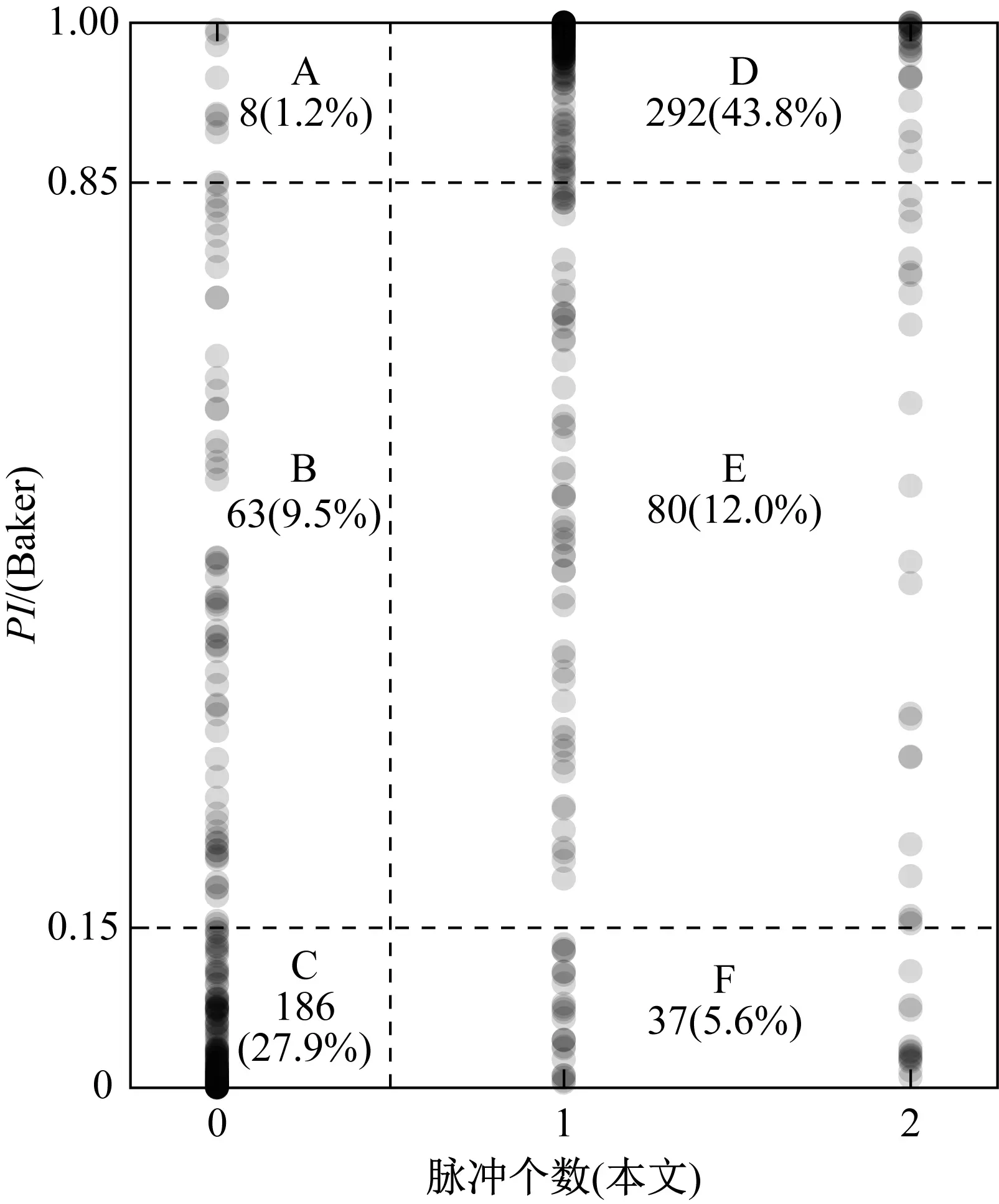
图8 本文与Baker的脉冲型地震动识别结果对比Fig.8 Comparison of the identified result between the proposed approach and Baker’s method

666条地震动中，样本主要分布在C和D区域，其中43.8%的记录(D区)被本文和Baker识别为脉冲型地震动。27.9%的记录(C区)被Baker识别为非脉冲型地震动，同时不被本文的方法定义为脉冲型地震动。冲突区域(A、F区)的样本数仅占总样本数6.8%，并且在F区，Baker的方法定义为非脉冲型地震的37条地震动记录中，13条记录被本文识别为双脉冲型地震动。

选择3条冲突区域(A、F区)的地震动记录，对比了由本文和Baker的方法提取的脉冲信号，如图9所示。并进一步分析两种方法的识别结果出现差异的原因：① 本文提取的单脉冲信号为一个周期的波形，而Baker的脉冲信号是多个周期的波形，这导致Baker的脉冲指标可能偏大，从而将没有显著脉冲波形的记录定义为脉冲型地震动(见图9(a))。② Baker提取的脉冲信号受到小波基的约束，因此脉冲信号与初始地震动的拟合较差，导致其识别结果出现错误，而本文的方法得到的脉冲信号与初始地震动速度时程的拟合更好，因此得到的脉冲指标更加可靠(见图9(b))。③ 当初始地震动速度时程中存在2个显著的脉冲波形时，Baker的脉冲指标偏小，从而将脉冲型地震动记录识别为非脉冲型地震动；而本文可以进一步提取双脉冲信号，从而识别出存在两个显著脉冲波形的脉冲型地震动(见图9(c))。

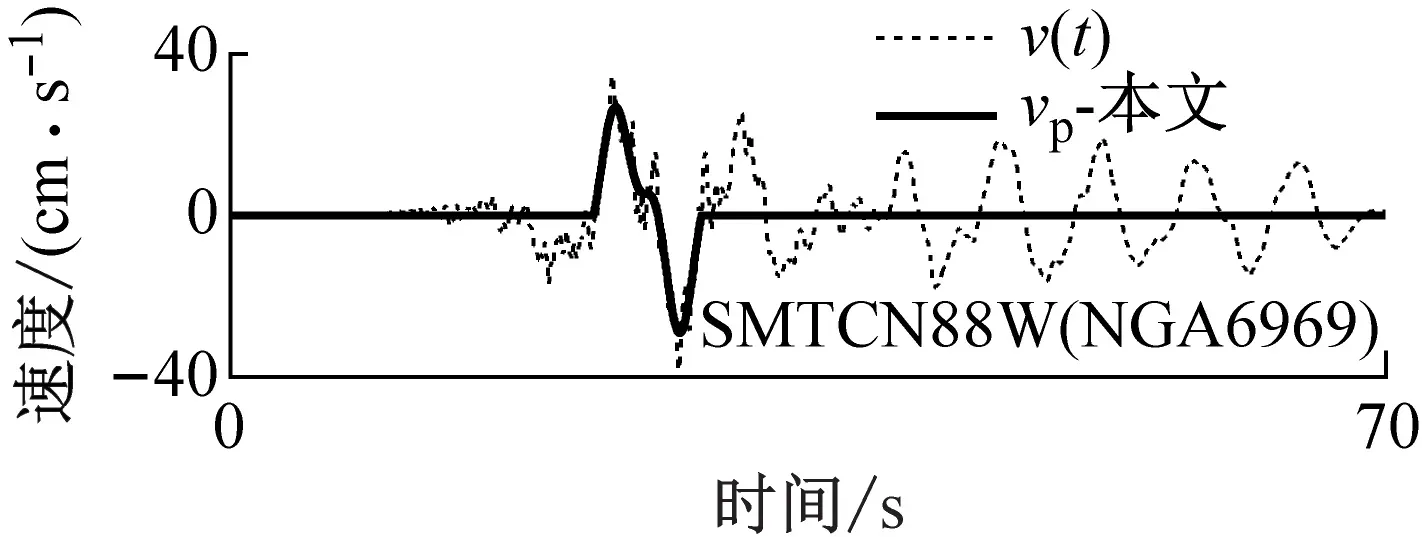
(a) A区域的地震动记录

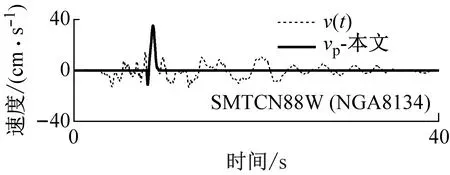
(b) F区域地震动记录(本文识别为单脉冲型)

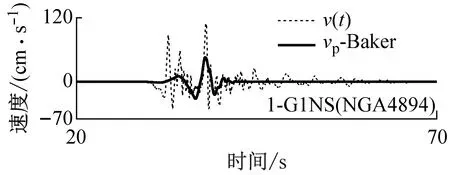
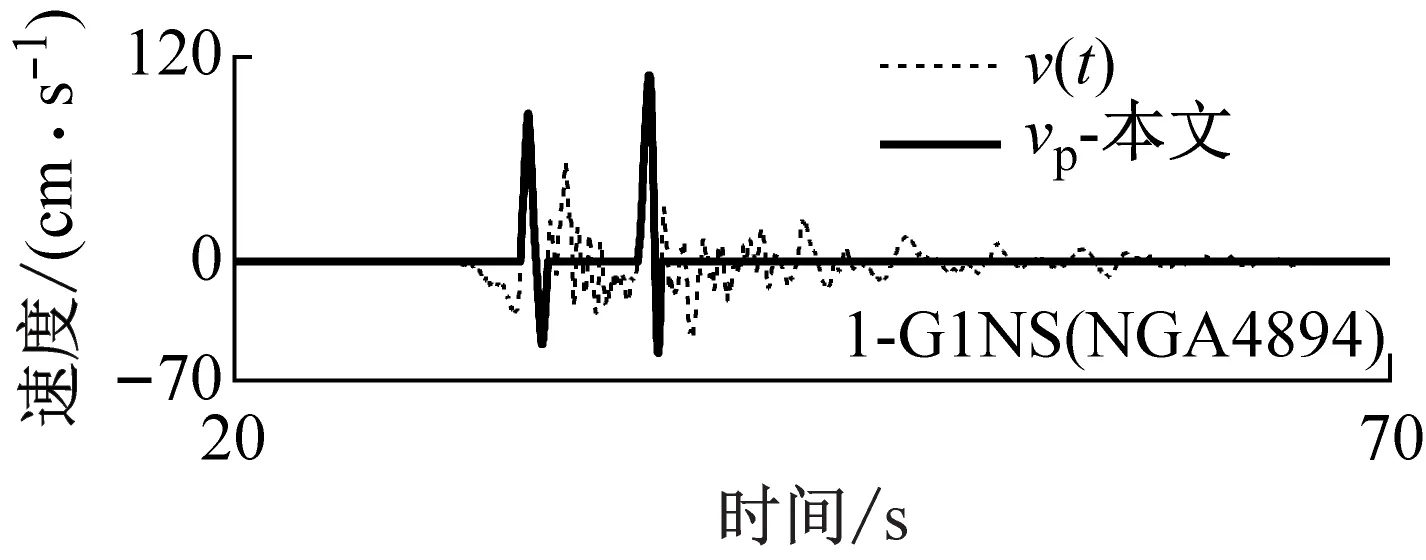
(c) F区域地震动记录(本文识别为双脉冲型)图9 本文方法与Baker的方法识别结果不一致的地震动Fig.9 Three typical ground motions with different classification results based on Baker’s and the proposed methods

3.2 与Zhai的方法对比

Zhai等[13]利用D&G脉冲模型和峰点法提取速度脉冲信号，并以脉冲能量作为地震动的识别指标(Ep)。Zhai和本文方法的近断层地震动分类结果对比，如图10所示。其中纵坐标为Zhai的识别指标Ep，Zhai量化识别脉冲型地震动的标准为：当Ep>0.3时，该记录为脉冲型地震动；当Ep≤0.3为模糊区域，表示该记录不被识别为脉冲型地震动。横坐标为本文方法的识别结果。图10基于Zhai和本文的分类结果划分为4个区域，并给出了各区域样本数目及占比。666条地震动中，样本主要分布在I和J区域，54.2%的记录(J区)被本文和Zhai的方法都识别为脉冲型地震动，33.6%的记录(I区)同时不被本文和Zhai的方法定义为脉冲型地震动。而结果冲突区域(H、K区)的样本数仅占总样本数12.2%。

图10 本文与Zhai的脉冲型地震动识别结果对比Fig.10 Comparison of the identified result between the proposed approach and Zhai’s method.

本文和Zhai的方法提取的脉冲信号对比，如图11所示。进而分析两种方法的识别结果出现差异的原因：① Zhai的方法只能拟合高度对称的脉冲波形，对非对称脉冲波形的地震动记录的识别误差较大(见图11(a))。而本文的方法得到的脉冲信号与初始地震动速度时程的拟合更好，因此识别结果更加可靠(见图11(a)和图11(b))；② Zhai的方法无法识别出存在两个显著脉冲波形的脉冲型地震动(见图11(c))。

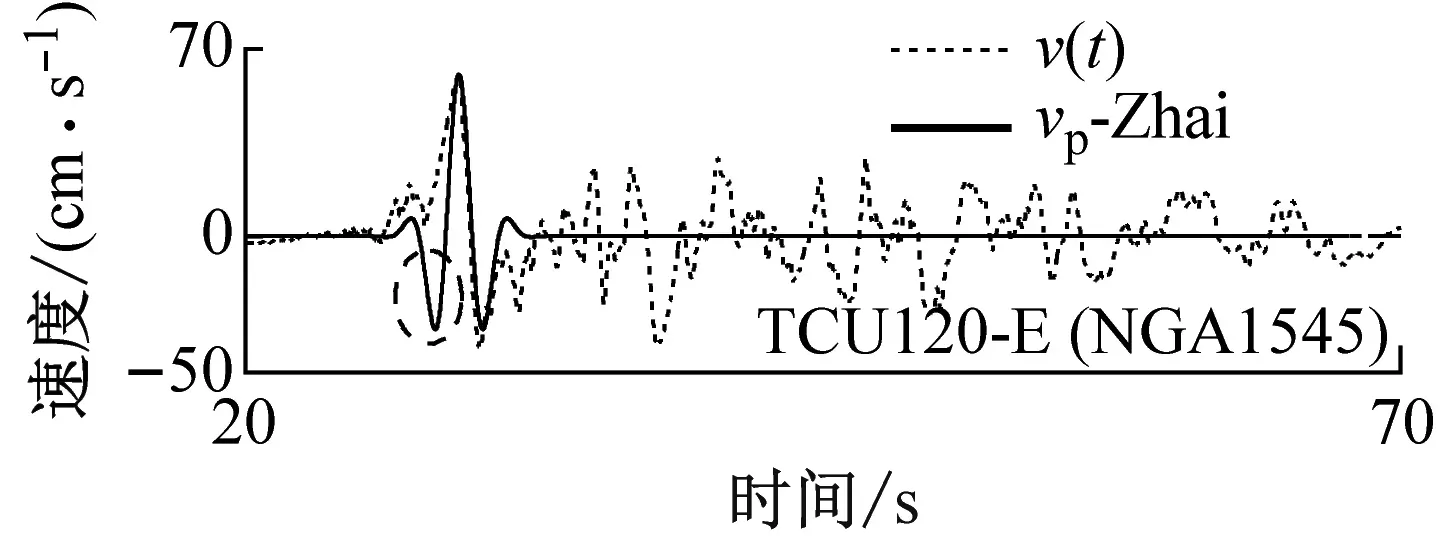
(a) H区域的地震动记录

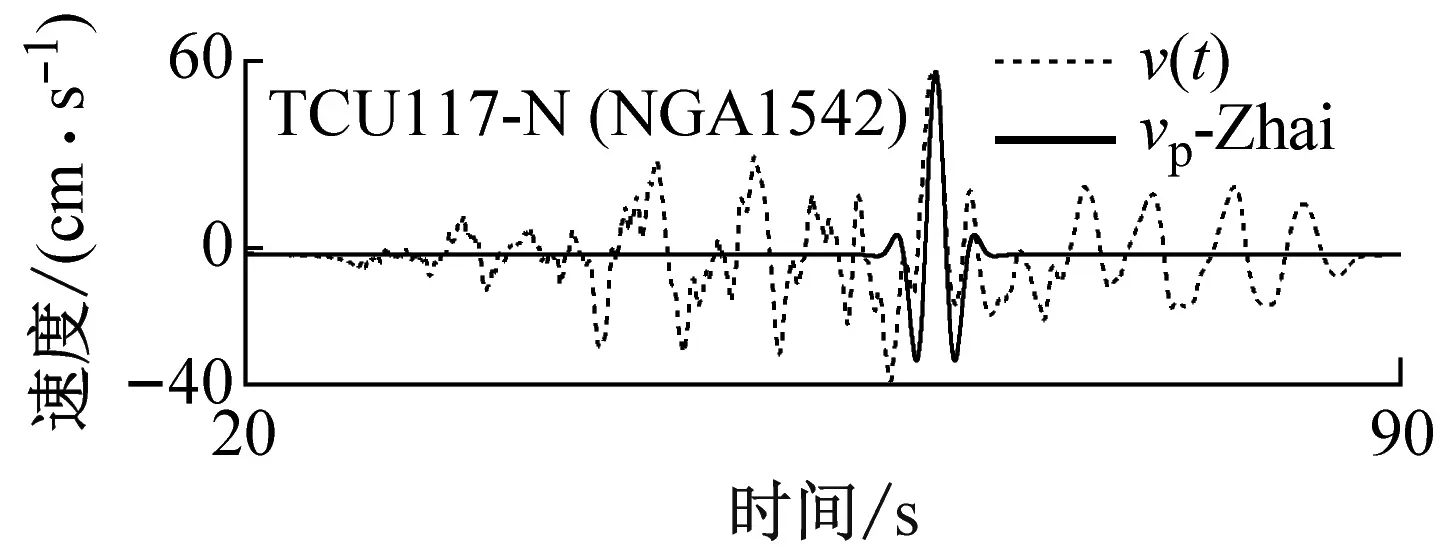
(b) K区域地震动记录(本文识别为单脉冲型)

(c) K区域地震动记录(本文识别为双脉冲型)图11 本文方法与Zhai的方法识别结果不一致的地震动Fig.11 Three typical ground motions with different classification results based on Zhai’s and the proposed methods

Baker、Zhai和本文的近断层脉冲型地震动的识别结果对比，如表1所示。总体来说，Baker、Zhai和本文的近断层地震动的识别结果比较接近。在666条地震动记录中：一共276条近断层记录被3种方法都识别为脉冲型地震动；只有3条(0.5%)记录不被本文识别为脉冲型地震动而被Baker和Zhai定义为脉冲型地震动；只有12条(1.8%)地震动不被Baker和Zhai定义为脉冲型地震动，而被本文识别为脉冲型，其中7条记录被本文识别为单脉冲型，5条记录被本文识别为双脉冲型。因为本文提取的脉冲信号与初始地震动拟合程度较Baker和Zhai的方法更好，所以对部分地震动的识别结果更加可靠。此外，本文可以提取双脉冲信号，并进一步识别出双脉冲型地震动，而Baker和Zhai的方法无法识别出存在两个显著脉冲波形的脉冲型地震动。

表1 本文与Baker、Zhai的脉冲型地震动识别结果对比Tab.1 Comparison of the identified result between the proposed approach with Baker’s and Zhai’s method

4 脉冲周期计算方法

脉冲周期与结构自振周期的比值对结构的响应有显著影响，所以脉冲周期的确定一直是研究人员关注的对象[10]。目前没有统一的计算脉冲周期的方法。一种常用的方法是利用速度反应谱峰值对应的周期作为该地震动记录的脉冲周期[27]，简称该方法为“Sv法”。Baker以最大小波系数的伪周期作为地震动记录的脉冲周期。Zhai利用脉冲模型拟合脉冲波形，并基于峰值法计算地震动速度脉冲周期。

本文基于Butterworth非因果低通滤波器和零点法提取脉冲信号，并以脉冲信号的持续时间计算地震动的脉冲周期，如式(9)。对于双脉冲型地震动记录，脉冲周期应为脉冲特征最显著的脉冲波形的持续时间，因此本文以相对脉冲能量指标Er较大的脉冲信号的持续时间作为双脉冲型地震动记录的脉冲周期。

Tp=te-ts

(9)

为了验证本文提出的算法得到的速度脉冲周期的有效性，本文选取了276条记录，这些记录被Baker、Zhai和本文的方法都识别为脉冲型地震动。然后采用Sv法、Baker、Zhai及本文的方法计算这些地震动记录的脉冲周期，4种方法计算得到的脉冲周期的比较,如图12所示。

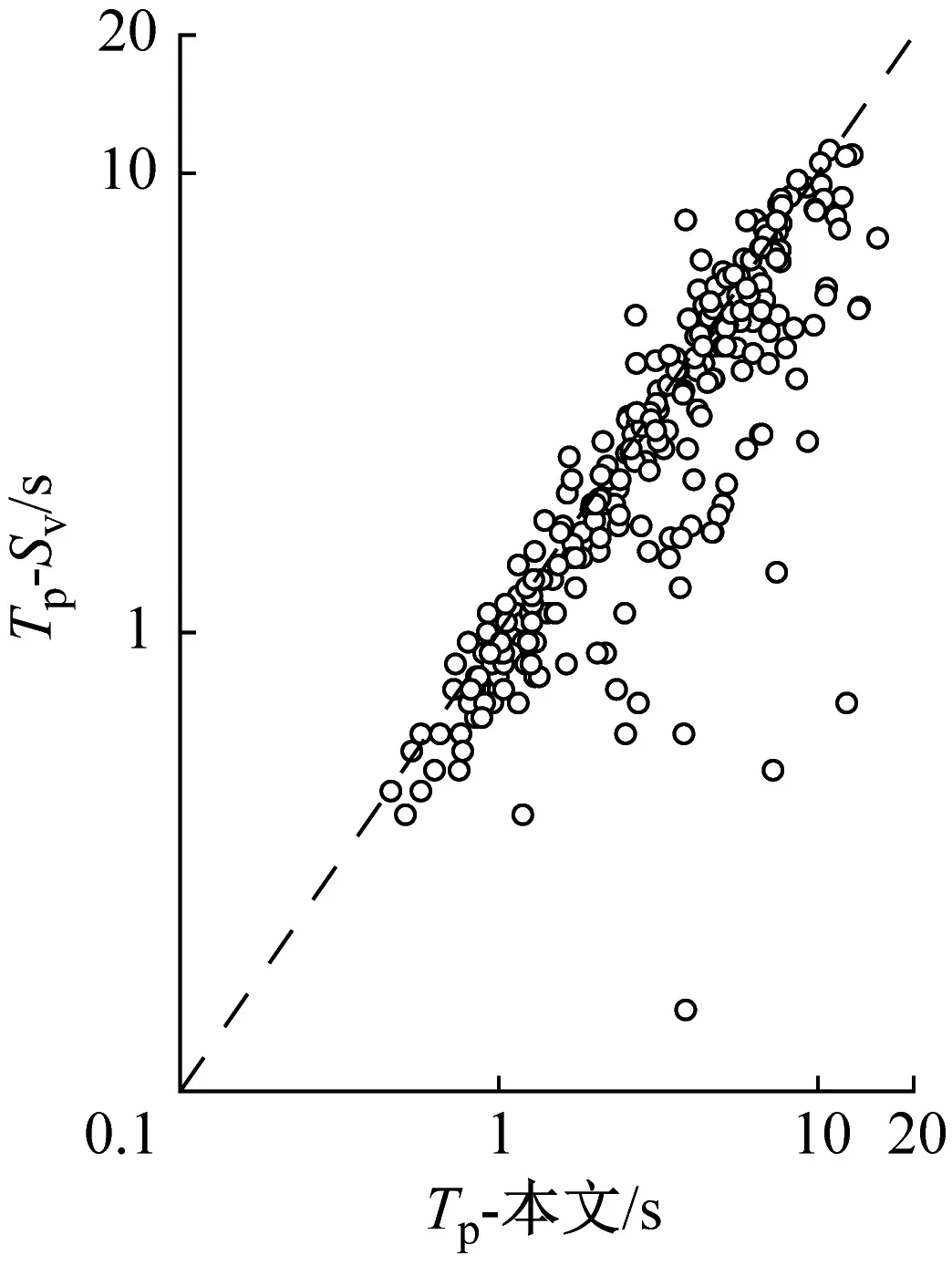
(a) 本文与Sv法对比

(b) 本文与Baker法对比

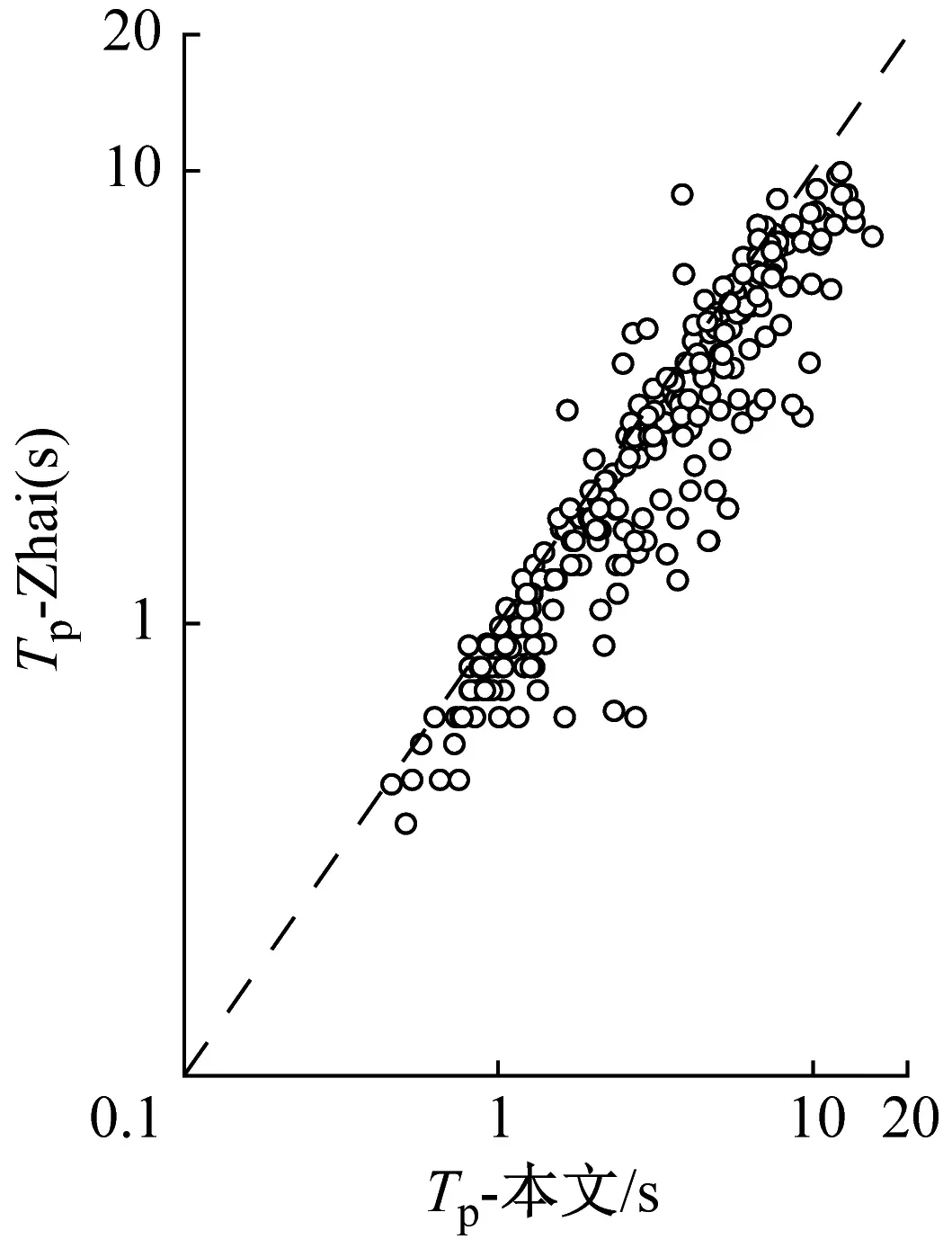
(c) 本文与Zhai法对比

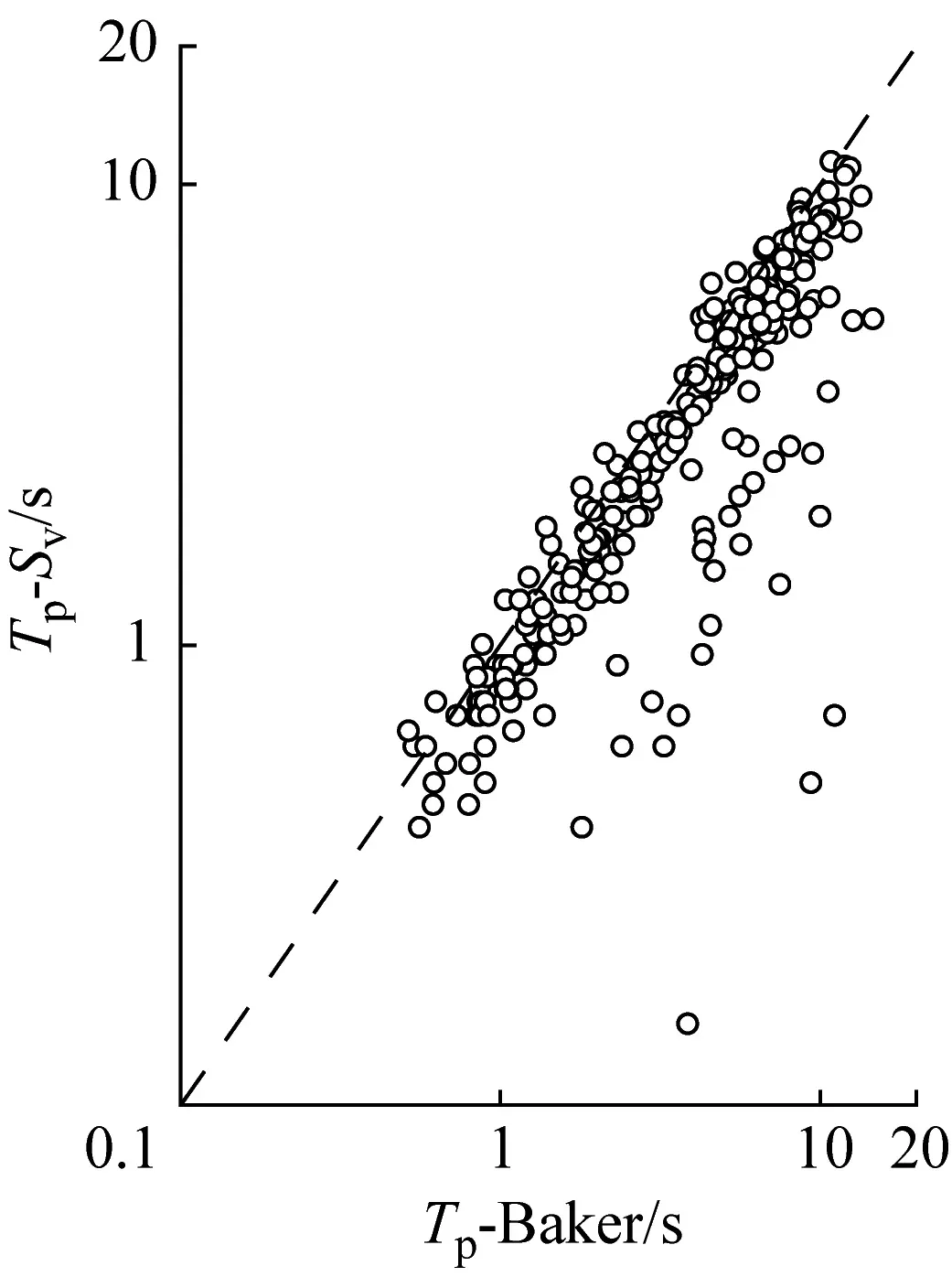
(d) Baker法与Sv法对比

(e) Zhai法与Sv法对比

(f) Zhai法与Baker法对比图12 本文方法与其他方法所得周期的对比Fig.12 Comparison of the pulse periods obtained by proposed method with 3 reference methods

总的来说，4种方法计算的脉冲周期基本相似，其中Baker得到的脉冲周期偏大于其他方法(见图12(b)、图12(d)和图12(f))，这是因为Baker以最大小波系数的伪周期计算脉冲周期，脉冲周期的取值受到小波基波形特征的影响，使得Baker得到的脉冲周期往往偏大。虽然Zhai和本文的方法都基于脉冲信号的持续时间计算脉冲周期，但由于两种方法脉冲提取方法和脉冲波形的不同，Zhai得到的脉冲周期会略小于本文的计算结果(见图12(c))。本文与Sv法得到的脉冲周期的值更相似(见图12(a))，介于Baker和Zhai的算法之间。值得注意的是，有一些特殊情况(见图12(a))，其中由本文方法得到的一部分地震动的脉冲周期与通过Sv法得到的脉冲周期有显著差异。通过对比图12(d)和图12(e)，Baker和Zhai的算法和Sv法也有一些显著差异的数据点，而这种现象在本文和Baker得到的脉冲周期比较时并不存在。这是因为Sv法所得脉冲周期会受到地震动中的高频分量的影响，而Baker、Zhai和本文的算法是根据可视脉冲波形来决定脉冲周期，所以在出现这种显著差异的情况下，基于本文方法得到的速度脉冲周期会更合理。根据以上比较结果，可以认为基于本方法得到的脉冲周期是可靠的。

5 结 论

(1) 应用Butterworth非因果低通滤波器过滤初始地震动中的高频分量，再基于零点法提取速度脉冲信号，并以脉冲信号中只存在一个极大值和一个极小值作为滤波器截止频率的确定标准。

(2) 通过本文方法提取的脉冲信号与初始地震动拟合效果较好，且操作简便，易于应用。本文方法不需要定义基函数，可以模拟不规则非对称的脉冲波形。此外，该方法还可应用于双脉冲信号的提取。

(3) 单脉冲型地震动的识别标准为：相对脉冲能量指标Er>0.32；双脉冲型地震动的识别标准为：Er>0.55且相对脉冲能量指标中的最小值应大于最大值的0.75倍，或者Er>0.55且二次脉冲信号的峰值和相对能量指标大于初次脉冲信号的75%和50%。

(4) 对于单脉冲型地震动记录，以脉冲信号的持续时间计算脉冲周期；对于双脉冲型地震动记录，以相对脉冲能量指标较大的脉冲信号的持续时间为脉冲周期。通过对比Sv法、Baker、Zhai及本文计算脉冲周期的方法，结果表明本文方法与Sv法得到的脉冲周期更加接近，并介于Baker及Zhai的方法得到的脉冲周期之间。