基于小波加权TSVR算法的OFDM系统信道估计
2020-07-13马艺梅王立东陈雪波吴文良
马艺梅,王立东,陈雪波,吴文良
1(辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114051) 2(聚龙股份有限公司,辽宁 鞍山 114051)
1 引 言
随着技术的进步和社会的发展,人们对在高速相对运动条件下实现数据高速可靠传输的需求日益迫切.然而由于高速移动环境易受到多径传播与时延扩展等因素的影响,信道传输特性劣化,在接收端会产生严重的符号间干扰(Inter-symbol Interference,ISI)和载波间干扰(Inter-carrier Interference,ICI),影响通信质量甚至无法正常通信[1,2].正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术是解决频率选择性信道所造成ISI问题的有效途径,因其具有频谱利用率高、抗多径干扰和脉冲噪声的优势,已经成为新一代无线移动通信系统中的关键技术.由于OFDM系统中信道估计的质量对于通信性能的影响较大,因此信道估计方法成为研究热点[3].在信道估计中,由于非盲信道估计精度高、易于实现等优点,使其成为主要被采用的技术[4,5].本文采用非盲信道估计方法对信道进行预测.基于导频的信道估计方法主要有基于最小二乘(Least Squares,LS),最小均方误差(Minimum Mean Square Error,MMSE)等准则来获取导频处的信道频率响应[6,7].文献[8]提出了线性插值(Linear)的方法来预测无导频处的子载波的信道频率响应,并对它们的性能进行了比较.插值算法内容简单,易于实现,但是其预测准确度不高.为了克服插值算法的不足[9],文献[10]提出一种能够解决高维问题和局部极小值问题,具有良好的泛化能力的支持向量机预测算法.支持向量机(Support Vector Machines,SVM)是以统计学习理论中的VC维和结构风险最小化原则为理论基础的一种机器学习方法.目前在求解分类和回归两方面问题中都得到成功应用[11].2007年,Javadeva等人在SVM的基础上提出了一种训练速度更快的新的分类方法,称为孪生支持向量机(Twin Support Vector Machines,TWSVM)[12].2010年Peng等人将TWSVM推广到了回归问题领域,提出了孪生支持向量回归机(Twin Support Vector Regression,TSVR)[13].在之后的一段时间内,TSVR取得很大的发展[14,15].本文改进了TSVR算法,提出了基于小波加权的孪生支持向量机回归(Wavelet Transform based Weighted TSVR,WTWTSVR)算法对信道参数进行估计.
此算法的创新点如下:
1)本文首次提出了WTWTSVR算法预测衰落信道的信息,在OFDM系统中,其性能优于传统的信道估计算法.与TSVR信道估计方法比,具有计算复杂度低、计算速度更快的优点.
2)WTWTSVR算法是传统TSVR算法的扩展,针对OFDM系统中非线性和时间序列衰落信道的抗干扰问题,此算法是在TSVR算法基础上引入了小波变换来计算训练数据的权值,为样本预处理提供了一个新的角度.小波变换是一种信号的时频表示方法,适合处理时频分析中的参数等时间序列信号.
3)利用小波变换理论确定权值矩阵和权值向量,并将其插入信道参数回归目标函数的二次和一次项中,以降低离群值的影响.权值矩阵和权值向量表示噪声样本的距离及其位置,它反映了训练样本的先验知识.对于噪声较大的样本,赋予较小的权值;对于噪声较小的样本赋予较大的权值.
2 系统框架
2.1 OFDM传输系统
图1为OFDM信道估计系统结构框图.设X(k),k=0,1,…,N-1为一个OFDM频域信号,N为子载波数量.经离散傅里叶反变换(Inverse Discrete Fourier Transform,IDFT)调制到时域.调制后的一帧时域OFDM信号可表示为式(1).
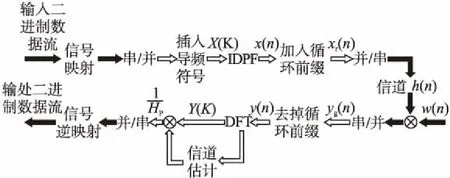
图1 OFDM信道估计系统结构框图
(1)
为了消除符号间干扰,每帧OFDM符号前插入循环前缀,并且循环前缀的长度大于信道的最大时延.通过时变的多径衰落信道后,输出的信号为式(2):
yg(n)=xg(n)⊗h(n)+ω(n)
(2)
式(2)中,xg(n)为发送的加入循环前缀后的OFDM信号,yg(n)为接收端接收到的OFDM信号,h(n)为信道的冲击响应,ω(n)为加性高斯白噪声,g为时域序列循环前缀标识,⊗表示卷积运算.在接收端,接收到的信号yg(n)的循环前缀被去除,得到的y(n)通过N点离散傅里叶变换(Disctrete Fourier Transform,DFT)后,输出的信号可表示为:
Y(k)=X(k)H(k)+W(k),k=0,1,…,N-1
(3)
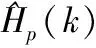
(4)
2.2 基于导频的OFDM信道估计算法
本文通过在时域和频域两个方向等间隔地插入导频信号,既保存了梳状导频对快衰落信道的优势,又考虑到频谱资源占用的合理性.采用的时频二维导频图案如图2所示.
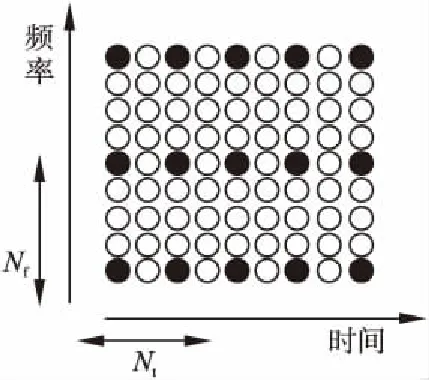
图2 导频插入方式
时频域内导频符号的设置必须使信道估计器能够跟上信道频率响应函数的变化,而又不过多地增加系统的额外开销.导频密度的下限由二维奈奎斯特(Nyquist)采样定理确定,即设时频方向上的导频间隔分别为It,和If,最大多径时延为τmax,最大多普勒频移为fdmax,OFDM符号的周期为T,子载波间隔为Δf,则时频域的导频间隔应满足[16]:
(5)
3 OFDM非线性系统孪生支持向量机回归模型(TSVR)
非线性支持向量回归机,即通过某一个非线性变换,将训练数据映射到一个高维线性特征空间,再进行线性回归,就可以得到原来样本空间的非线性回归值.在SVR的基础上,TSVR把一个凸二次优化问题转化为两个小的凸二次优化问题,从而提高算法运行速度,减少算法复杂度[13].
假设一个样本(x,y)∈Rn是一个n维向量,其中x∈Rn,y∈R,则m个这样的样本可被表示为(x1,y1),…,(xm,ym),令A=[x1,…,xm]T∈Rm×n,Y=[y1,…,ym]T∈Rm,分别为训练样本的输入数据组和其对应的输出数据组,e=[1,…,1]T是一个全为1的向量,K(.,.)表示一个核函数,则K(A,AT)就是一个m×m的核函数矩阵,矩阵的第i行第j列(i,j=1,2,…,m)可以表示为:
[K(A,AT)]i,j=K(xi,xj)∈R.
(6)
采用高斯径向基函数作为核函数:
(7)
其中σ是带宽,用于控制高斯核函数的局部作用范围.回归函数的下界f1(x)=K(xT,AT)ω1+b1,上界为f2(x)=K(xT,AT)ω2+b2,最终回归函数为两个函数的均值:
(8)
由K(xT,AT)=(K(x,x1),K(x,x2),…,K(x,xl))可知K(xT,AT)是一个m列的实数向量,ω1,ω2∈R是一个m行的实数向量,b1,b2∈R是一个偏差值.
3.1 基于小波变换的非线性孪生支持向量机回归模型(WTWTSVR)
WTWTSVR优化问题描述如下:
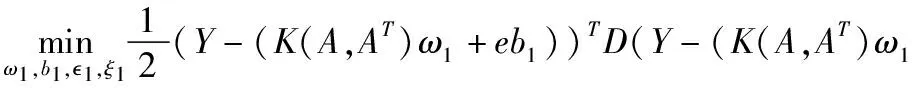
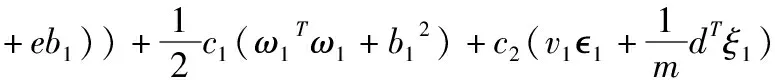
s.t.Y-(K(A,AT)ω1+eb1)≥-1e-ξ1
ξ1≥0e1≥0
(9)
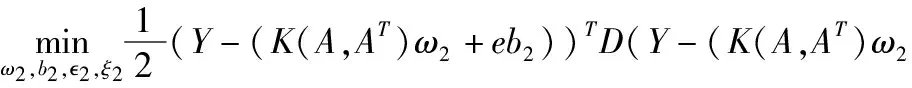
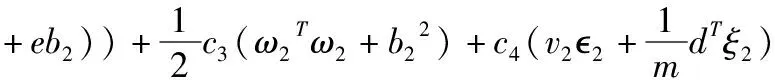
s.t.Y-(K(A,AT)ω2+eb2)≥-2e-ξ2
ξ2≥0e2≥0
(10)
式(10)中c1,c2,c3,c4,v1,v2≥0这些参数均为调节参数,1和2是非敏感参数,ξ1和ξ2是松弛向量,m是训练样本点数,d∈Rm是一个权值向量,其对角化矩阵D是一个权值矩阵(D=diag(d)∈Rm×m),为了解决式(9)的二次规划问题(QPPS),定义拉格朗日函数为:
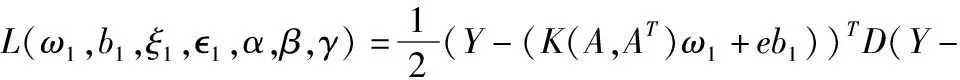
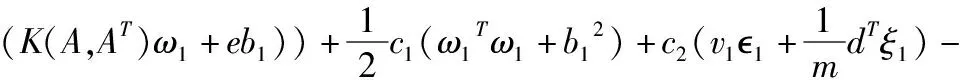
αT(Y-(K(A,AT)ω1+eb1)+1e+ξ1)-βTξ1-γ1
(11)
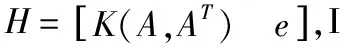
(12)
(13)
解式(12)和式(13)得ω1,b1及ω2,b2的表达式为:
[ω1Tb1]T=(HTDH+c1I)-1GT(DY-α).
(14)
[ω2Tb2]T=(HTDH+c3I)-1GT(DY+λ).
(15)
根据式(14)和式(15),代入式(8),我们便可以得到最终的回归函数.
3.2 权值矩阵D及系数向量d的确定
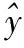
(16)
小波变换是一种时频分析的方法.小波函数适用于短时信号处理,这是大多数时间序列信号的特点.小波变换求估计值向量分为对信号进行小波分解、信号处理以及信号重构三个部分.用一系列滤波器计算了信号采用离散小波变换分解到第l步时的信号为yal,样本通过一个具有脉冲响应的低通滤波器φ(t),得到信号的低频部分yal+1和一个具有脉冲响应ψ(t)的高通滤波器,从而得到信号的高频部分ydl+1.
(17)
(18)
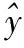
(19)
算法过程:
1)由公式(1)-公式(4)可以得到OFDM系统导频子载波处的频率响应估计值,并将其送入信道估计器中;
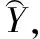
3)由公式(12)-公式(15)式子可以得到回归函数表达式u1和u2,再带入公式(8)便可得到一个OFDM符号中的全部子载波处的信道频率响应估计值.
4 仿真结果
为了验证所提出的WTWTSVR方法对OFDM信道双选择信道估计的性能,本节对信道估计中的经典算法:线性插值算法[8],TSVR算法[13]及对TSVR改进后的WTWTSVR算法和理想信道的误比特率(Bit Error Rate,BER)和均方误差(Mean Square Error,MSE)进行对比,得到相应的曲线.瑞利信道模型是无线通信信道基础的仿真模型.一般情况下,在瑞利衰落的状态下,多普勒功率谱具有Jakes功率谱密度函数,考虑频率选择性时变多径衰落的信道冲激响应模型[19],该模型可以表示为:
(20)
hl(t)表示第l条路径复衰减的脉冲响应,τl是OFDM符号个数为16,载波数为64,L=8,Monte Carlo实验次数为100,调制方式为16QAM,采样时间间隔为72μs,载波频率2.15GHz.为了降低变量参数选择的复杂度,令WTWTSVR中c1=c3,c2=c4,v1=v2;TSVR中C1=C2,1=2.
图3为几种情况下的SNR-BER及SNR-MSE性能图.图3(a)、(b)carrier_inter=2,symbol_inter=2时,多普勒频移分别为120km/h和350km/h,不同算法及理想状态下的信道误码率性能曲线图;图3(c)、(d)carrier_inter=4,symbol_inter=4时,多普勒频移分别为120km/h和350km/h,不同算法及理想状态下的信道误码率性能图;图3(e)、(f)表示多普勒频移为120km/h和350km/h时,不同SNR下载波间隔与误码率性能曲线图.表1、表2为不同算法的误码率及均方误差的具体数值及参数值.从图3中可以发现,在carrier_inter=2,symbol=2时,WTWTSVR算法相对于其他算法来说,在MSE和BER两个指标上都体现出了更高的准确率和更好的性能;在carrier_inter=4,symbol=4时,WTWTSVR算法在高信噪比下,优势明显.这说明权值矩阵和权值向量在目标函数中的应用是有效的.可以看出,信噪比一定时,载波间隔越大,误码率越高;载波间隔一定时,信噪比越高,误码率越低.
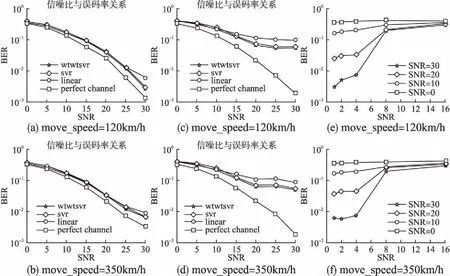
图3 不同算法的信道误码率性能图
表1 不同算法信道频率响应的MSE值
Table 1 MSE values of channel frequency responses of different algorithms

MSEcarrier_inter=2,symbol_inter=2;carrier_inter=4,symbol_inter=4.(km/h)120350120350WTWTSVR0.00180.00200.08630.0655TSVR0.00200.00220.10250.0785Linear0.00430.00460.18450.1468
表2 不同算法信道频率响应的BER值
Table 2 BER values of channel frequency responses of different algorithms
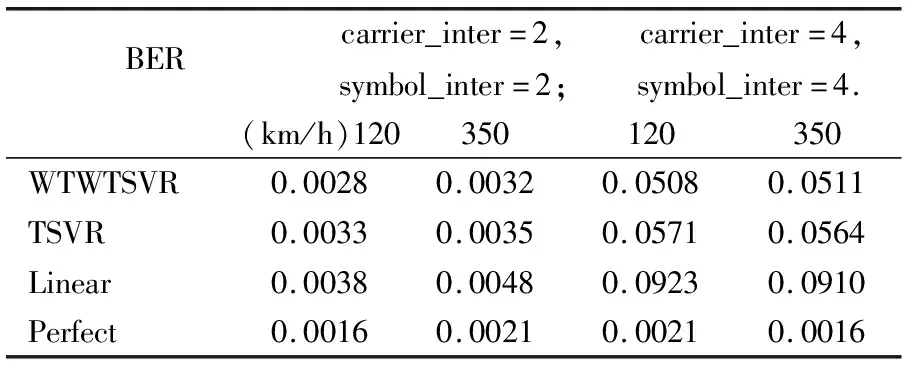
BERcarrier_inter=2,symbol_inter=2;carrier_inter=4,symbol_inter=4.(km/h)120350120350WTWTSVR0.00280.00320.05080.0511TSVR0.00330.00350.05710.0564Linear0.00380.00480.09230.0910Perfect0.00160.00210.00210.0016
5 总 结
本文提出了基于小波加权TSVR算法的OFDM统信道估计,对不同位置样本噪声赋予不同的权值,得到权值矩阵D和权值向量d.将D和d引入到TSVR的目标函数中,以此建立WTWTSVR模型来预测无导频处的子载波的信道频率响应.将WTWTSVR、TSVR和Linear几种算法在不同导频间隔、不同多普勒频移的情况下进行对比,结果表明:支持向量机回归算法性能优于插值算法,而WTWTSVR算法在TSVR的基础上具有更高的准确率,回归效果更好.
