2，4，6-三硝基-3，5-二氟苯酚热分解动力学

2020-07-11刘玉存荆苏明

含能材料 2020年7期

杨雷，刘玉存，荆苏明

（中北大学环境与安全工程学院，山西太原 030051）

1 引言

炸药的热性能直接决定了其能否应用到现代武器装备中，因此寻求具有良好耐热性能的炸药是含能化合物发展的需要［1-2］。含氟类化合物的合成研究一直是合成化学的热点，由于C—F 键具有较低的最高占据分子轨道（HOMO）和最低未占据分子轨道（LUMO）能级，所以其表现出“难氧化，易还原”的特点，C—F 键的HOMO 能量低，表明氟原子核对电子的束缚能力强，电子云分布不易受到外界的影响，从而导致其极化能力弱，从而影响化合物的沸点、溶解度、脂溶性以及表面张力等宏观物理性质［3-4］。C—F 键是最强的化学键之一，并且随着氟原子增多C—F 键会增强［5-8］。将C—F 键引入到芳香环上在药物合成中经常使用，相对于C—X 键，氟的吸电子能力更强，可以稳定芳香亲核取代过程中的芳基负离子中间体，使反应更容易进行，所以将氟原子或含氟基团引入到含能化合物的合成中是一种很有前景的发展方向［9-11］。

2，4，6-三硝基-3，5-二氟苯酚是本课题组自主合成的一种新型高密度含能化合物，其实测晶体密度为1.940 g·cm-3，相对于2，4，6-三硝基苯酚（苦味酸1.76 g·cm-3）有很大的提升，这是由于氟原子与氢原子能够形成分子内氢键，压缩分子体积，使分子的密度提高。其次，氟原子还能与氢形成分子间氢键，有助于增大分子间的晶格能，提升化合物的稳定性。为了研究该化合物的热稳定性，本研究采用TG-DTA 技术对2，4，6-三硝基3，5-二氟苯酚的非等温热分解过程进行了分析，分别采用了Kissinger 法、Flynn-Wall-Ozawa（F-W-O）法、Doyle 法和Satava-Sestak 法计算该物质的非等温热分解动力学数据，求出了其热分解反应过程的活化能和指前因子，并推测了其可能的热分解反应的机理函数和动力学方程，为其在火炸药中的应用奠定基础。

2 实验部分

2.1 实验材料

2，4，6-三硝基-3，5-二氟苯甲醚（自制）。IR（KBr：ν/cm-1）：3157.07，1631.90，1583.12，1533.16，1337.91，1169.33，916.43，702.59，667.82，637.63，609.93；元素分析C6HO7N3F2（%）：实测值（计算值）C 26.18（25.54），H 1.68（1.43），N 18.89（19.86）。

铟（99.99%）和锌（99.99%）用于校准设备，α-Al2O3粉末用作TG-DTA 的标准材料（日本岛津公司）。

2.2 仪器和方法

TG-DTA 分析采用北京恒久科技HCT-1 热分析仪，分析前，测量标准样品校准仪器。测量标准的标本如铟（纯度=99.99%，Tm=429.78 K，ΔmH=28.45 J·g-1）或锌（纯度=99.99%，Tm=419.58 K，ΔmH=100.50 J·g-1）完成温度的校正，在热分析天平两端放置两个空坩埚进行基线的校准。α-Al2O3为标准参考物。在氮气（30 mL·min-1）的氛围下分别以升温速率5，10，15，20 K·min-1对化合物的TG-DTA 曲线进行分析，升温范围为室温至673.15 K，试样量为3.0～3.2 mg。

2.3 动力学方法

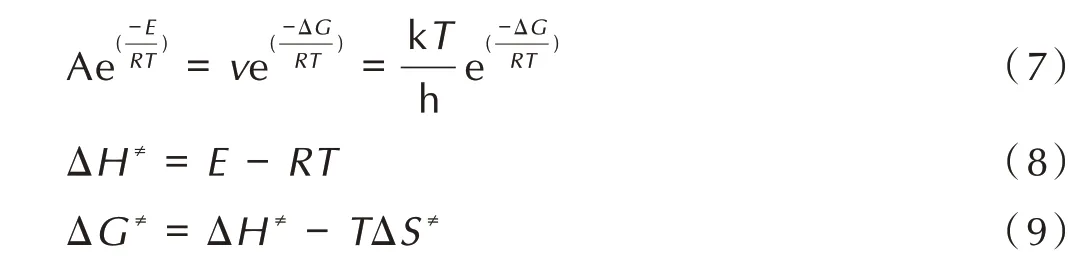
式中，v为爱因斯坦振动频率；k 为玻尔兹曼常量，1.3807×10-23J·K-1；h为普朗克常量，6.625×10-34J·s。

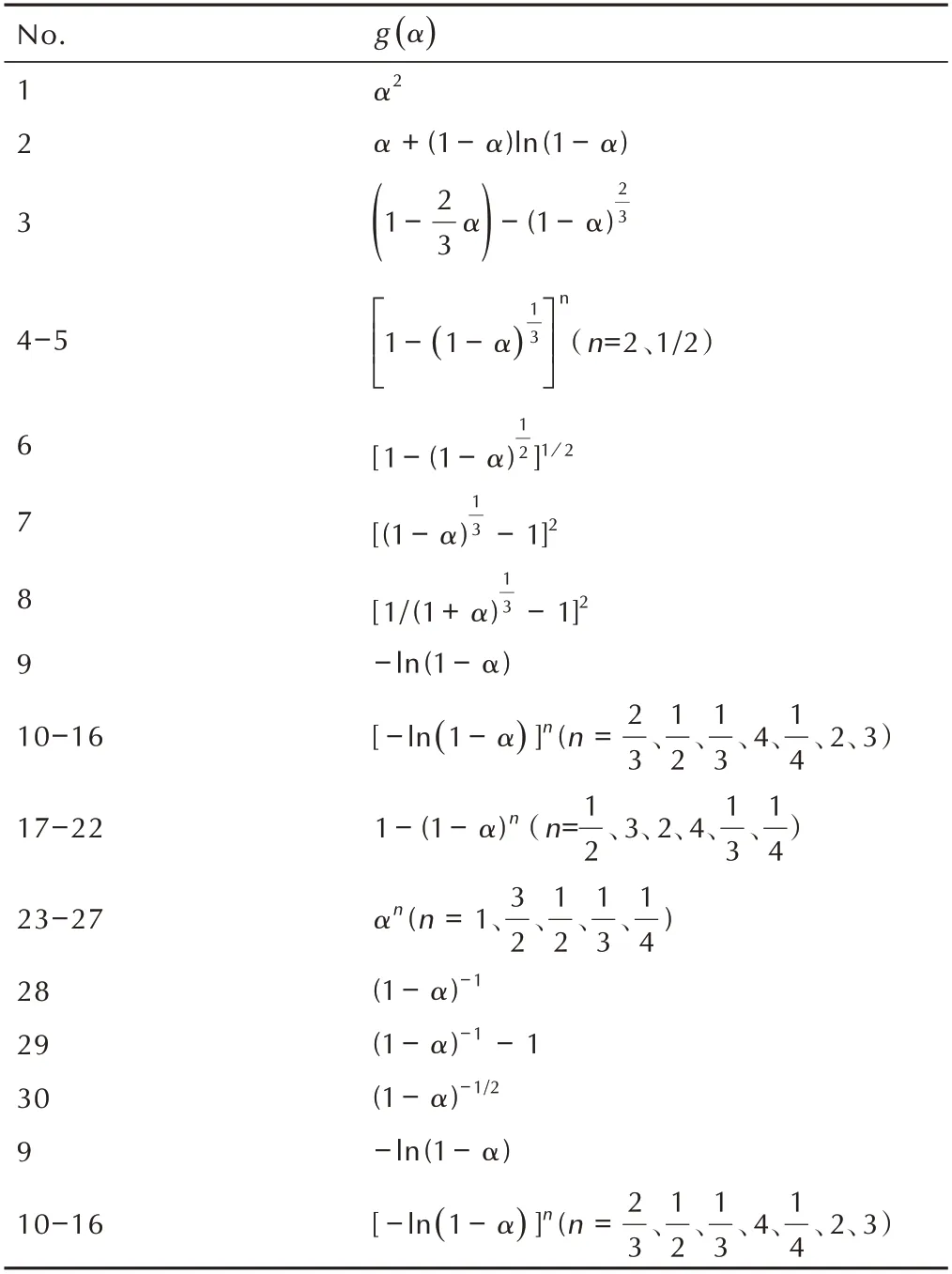
表1 各种动力学模型g（α）的函数表达形式Table 1 The algebraic expression of g（α）for the various kinetic reaction models

3 结果与讨论

3.1 2，4，6-三硝基-3，5-二氟苯酚的热分解过程

2，4，6-三硝基-3，5-二氟苯酚在升温速率分别为5，10，15，20 K·min-1下的DTA 和TG 曲线分别如图1和图2 所示。从图1 可以看出，在不同的升温速率下，三硝基二氟苯酚的分解峰温在479.65～500.85 K，随着升温速率的提高，分解峰温也有升高，其平均值为491.25 K。由图2 可以看出，该物质的热分解伴随着快速的质量损失，平均质量损失率为73.59%，其中2，4，6-三硝基-3，5-二氟苯酚的热分解起始温度在474.35～486.25 K，说明升温速率对起始热分解温度影响较小。值得注意的是在DTA 曲线中，起始分解温度之前有一个小的吸热峰，推测是由于三硝基二氟苯酚在升温的过程中发生了晶型的改变，所以在开始分解之前有一个短暂的吸热过程，这对三硝基二氟苯酚的晶型转变研究有一定的参考意义。

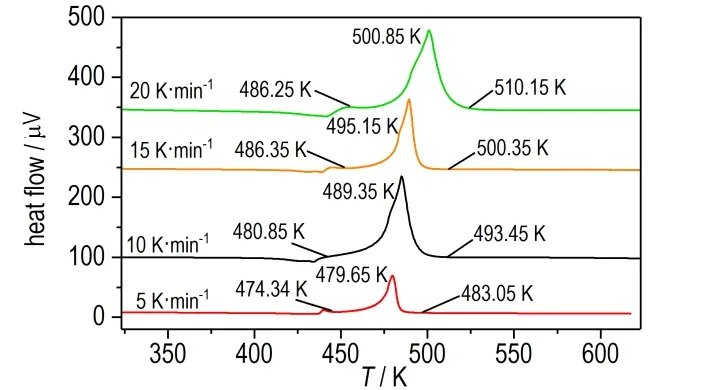
图1 三硝基二氟苯酚的DTA 曲线Fig.1 DTA curves of 2，4，6-trinitro-3，5-difluorophenol

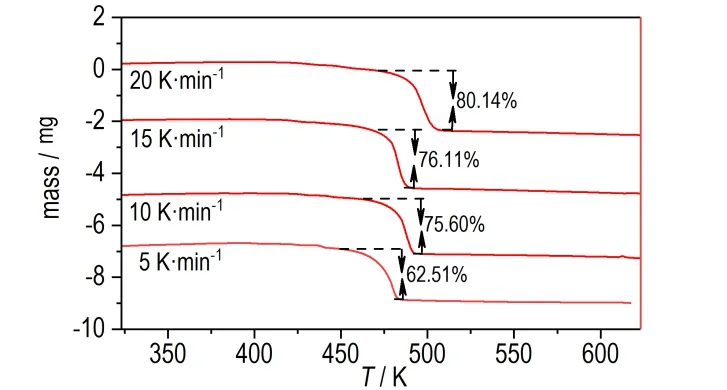
图2 三硝基二氟苯酚的TG 曲线Fig.2 TG curves of 2，4，6-trinitro-3，5-difluorophe

3.2 2，4，6-三硝基-3，5-二氟苯酚的非等温动力学

由图1 可知，三硝基二氟苯酚的分解温度随着升温速率的提升逐渐上升。采用F-W-O、Doyle、Kissinger和Satava-Sestak 等方法研究了该化合物的非等温分解动力学，得到了其活化能和指前因子等相关参数。由Kissinger 方法得到的活化能为124.28 kJ·mol-1，指前因子1.13×1010min-1，线性相关系数R2=0.996。采用F-W-O 和Doyle 法得到的活化能见表2，两种方法所得活化能的平均值为120.94 kJ·mol-1。

采用Satava-Sestak 法结合30 种不同的机理函数所计算出来的活化能和指前因子，再根据用F-W-O 方法和Doyle 方法得出的活化能以及Kissinger 方法得到的指前因子比较，满足条件| (E0-Es)/E0|≤0.1 和| (lnAs- lnAK)/lnAs|≤0.46，得到正确的反应机理函数（表1 中第25 种形式）。该机理函数的积分方程和微分方程的形式为g（α）=α1/2，f（α）=α-1/2。根据该方法所得的活化能和指前因子分别为126.06 kJ·mol-1，和1.64×1016min-1

所以，根据以上四种方法所得的活化能和指前因子求得2，4，6-三硝基-3，5-二氟苯酚活化能的平均值为123.06 kJ·mol-1，指前因子1.37×1013min-1。

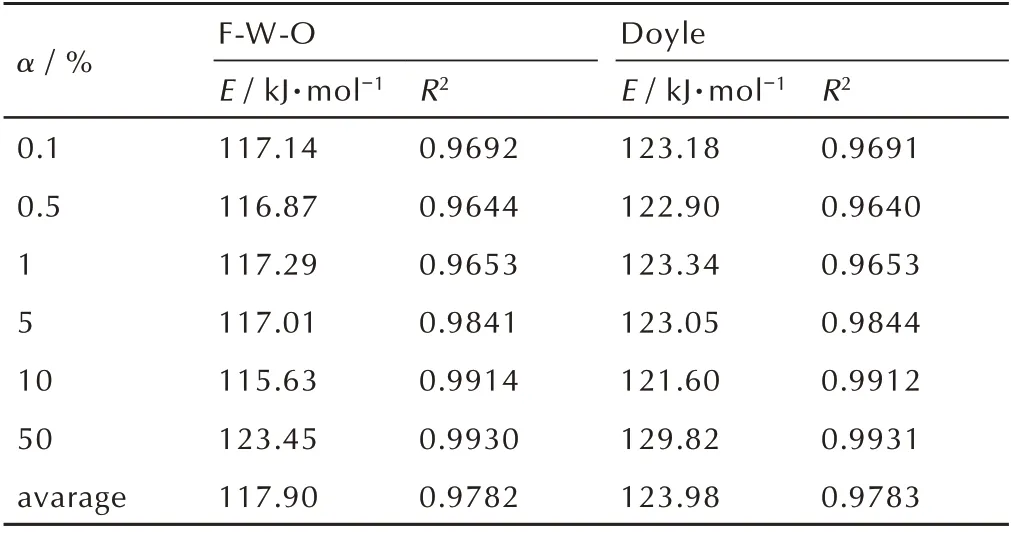
表2 F-W-O 和Doyle 法所得活化能Table 2 The activation energy was obtained by F-W-O and Doyle method

3.3 热力学参数

将上面所得的活化能E（123.06 kJ·mol-1）和指前因子A（1.37×1013min-1）代入式（7）、式（8）、式（9）中，其中T为分解峰温的平均值（T=491.25 K）得到活化焓ΔH≠，活化熵ΔS≠以及活化吉布斯自由能变ΔG≠分别为122.65 kJ·mol-1，121.46 J·mol-1·K-1和62.98 kJ·mol-1。