“游在杭州学数学”整合性课程的开发与实践

沈洋

【摘   要】将游学活动与国家课程进行整合性开发是当下课程改革的亮点。“游在杭州学数学”整合性课程是以小学数学课程为核心，整合其他学科知识，针对杭州10个数字景点，从“数与代数”“图形与几何”“统计与概率”“综合与实践”四个维度开发的游学课程，旨在通过项目式学习培养学生综合运用知识解决实际问题的能力，在过程与结果相结合的课程评价中促进学生数学素养的提升、创新能力的发展。

【关键词】游学活动;小学数学;整合性课程

《义务教育数学课程标准（2011年版）》指出，数学课程能为学生未来生活、工作和学习奠定重要的基础。但是现在的一些数学课往往在教学活动类型设计上存在不足，类似于现场考察、参观访问的内容较难实施。数学课程理应具有开放性，即将学生的数学学习置于广阔的生活背景中，引导学生广泛利用家庭、社会、自然资源进行数学学习，形成整合性课程，使课内外知识联系更紧密，学习更有效。

杭州是世界著名的旅游城市和历史文化名城，其中有不少带有数字的景点。因此，教师可以根据数学课程的开放性，梳理有关数字景点的游学活动与数学课程内容的衔接点，并与其他学科知识适当融合，开发以小学数学学科为核心的“游在杭州学数学”整合性课程，将数学课延伸到更为广阔的生活领域，在游学活动中提升学生的数学素养。

一、课程目标：综合运用知识解决实际问题

“游在杭州学数学”整合性课程，旨在通过对杭州数字景点的实地考察、现场体验、访谈等，综合运用所学知识解决实际问题，并由此产生学习动力与兴趣，在解决问题的过程中拓展学科知识，培养学生的学科思维和人文精神，促进学生综合素养与能力的发展。

二、课程内容：以数学为核心，整合多学科知识

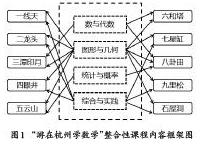
“游在杭州学数学”整合性课程内容是以小学数学课程为核心，针对杭州10个数字景点，从“数与代数”“图形与几何”“统计与概率”“综合与实践”四个维度中选择2—3个进行整体架构（见图1）。

以“六和塔”游学课程为例，其教学内容涉及“数与代数”“图形与几何”两个维度，包括学会观察立体图形，并运用所学的几何知识进行推理验证;在实际情境中进行长度、角度的测量;选择合理数据进行组合图形面积的计算;应用比例知识估测塔的高度。这些课程内容与人教版四年级上册第三单元“角的度量”、人教版四年级下册第二单元“观察物体”、人教版五年级上册第六单元“多边形的面积”、人教版六年級下册第四单元“比例”等数学教材内容有契合点。

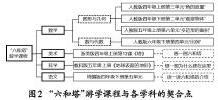
“游在杭州学数学”整合性课程内容主要与数学学科知识相关，但也注重整合其他学科的知识，整体架构课程内容。例如，“六和塔”游学课程内容分别与美术、科学、语文等学科内容进行了整合（见图2）。

三、课程实施：项目式学习为主，在实践中学数学

项目式学习是一种以学生为中心的教学方式。“游在杭州学数学”整合性课程按照学生参观景点的路线顺序设计由远及近、由外到内、由易到难的任务单，引导学生积极收集信息、获取知识、探讨方案，在实践中解决具有现实意义的问题，提升学生数学学科素养。

在“六和塔”游学课程中，教师按照游学路线设计“画一画”“想一想”“记一记”“验一验”“量一量”“算一算”6个不同难度的实践任务，其中以“量一量”“算一算”“测一测”任务难度最大。

（一）量一量角度，综合应用几何知识

实际情境中测量景区六和塔正八边形地基的内角度数，是根据人教版四年级上册第三单元“角的度量”设计的。学生拿到任务单时，认为并不难。但在现实情境中，学生遇到的“角”多为破损的、错位的、难以使用工具测量的等（见图3）。

看似简单的角度测量，颇具挑战性。学生必须深刻理解“角”的概念，综合应用所学的平行、延长线段、三角形的内角和等几何知识进行推理和操作，对这些特殊的角进行“补救”，才能完成任务。面对一系列奇奇怪怪的现实问题，学生一开始有点不知所措，在小组讨论商议以后，很快各个小组想出了不同的解决方案（见图4）。

  各小组解决方案

“量一量角度”的小组解决方案在现实情境中，没有人会明确告诉学生如何测量。但在任务驱动下，学生在反复地测量和讨论中，逐渐统一了小组意见，找到了正确的方法。看似简单的测量，不但锻炼了学生实际的操作和推理能力，合作意识和协作能力也得到了历练。这样的游学课程不仅有趣味性，有数学味，更能在合作中培养学生懂得分享、乐于奉献、待人宽容、敢于担当的品质。

（二）算一算面积，基于实际优化方案

根据人教版五年级上册第六单元“多边形的面积”所学知识，计算六和塔正八边形的地基面积并不难，方法也很多（见图5）。学生可以自主选择测量方法获取所需的数据。有些方法看似简单，但在实际测量时就会碰到麻烦，如方案1中需要测量底边中点到中心点“O”的距离，但是六和塔的中心点“O”被砖石包围，无法进入测量，怎么办呢？

  “算一算面积”的优化方案

学生平时作业中的“问题解决”终究有点“纸上谈兵”，往往会忽视在实际情境中的可行性。而游学活动就给学生提供了在实际情境中检验自己方案可行性的机会，有助于培养学生思考问题的全面性和严谨性。学生在实践操作中不断优化可行性方案，让书本知识与实践经验有机地结合起来，学习变得更立体，探究变得更有创造性。

（三）测一测高度，提升应用和创新能力

根据人教版六年级下册第四单元“比例”的知识来估测六和塔的高度，这一任务对于六年级学生来说行不行呢？学生一开始想到的方法与课本第63页的练习题3（见图6）有点相似，即通过测量同学的身高、同学的影长和六和塔的影长，运用正比例的知识可以求出塔高=同学的身高×塔的影长÷同学的影长。

 练习题3

游学那天虽然是个好天气，但是六和塔四周都是高大的植被和山體，学生在地面上找不到塔顶的影子，所以这个方案是不可行的。在教师的指导下，学生想到了等腰直角三角形的特性——两条直角边是相等的，于是借助所带的等腰直角三角板，让A学生的眼睛、B学生举的2米杆子顶端和塔的顶端成一条线，与地面、塔高共同构成了一个大的等腰直角三角形，塔的高度就是A学生到塔的中心点的距离加上B学生身高（见图7）。通过测量，A学生到六和塔中心点的距离是57.8米，B学生的身高是1.6米，总和是57.8+1.6=59.4米，得出的数据与实际塔的高度59.95米非常接近。在这样的估测中，学生运用了自己所学的平面几何的知识，锻炼了综合应用能力，创造力与核心素养也得到了提升。

  “测一测高度”示意图

四、课程评价：兼顾过程与结果，多维评价结合

“游在杭州学数学”整体性课程评价分为过程性评价和结果性评价两部分。过程性评价旨在建立安全机制，确保学生安全;引导学生学会学习、学会合作、学会交流;培养学生的公民意识，激发学生爱祖国、爱家乡的情感。例如，“六和塔”游学课程的过程性评价表从时间观念、学习态度、纪律意识、文明礼仪四个方面进行评价，占比60%（见表1）。

“六和塔”游学课程的过程性评价表

[评价项目 评价内容 分值 时间观念 能做到守时，不无故迟到、早退及缺勤 10 学习态度 准备充分，态度积极，能按时完成游学任务单 20 纪律意识 听从教师管理，有大局意识，遵守公共场所的秩序 10 文明礼仪 注重礼仪规范，严于律己，乐于助人，维护良好的小学生形象 20 ]

结果性评价分两部分：一是任务单的完成情况。完成难度不同的任务单可以得到不同数量的★。以“六和塔”游学课程为例，教师设计了6张任务单，共设置了20颗★。学生在游学结束后要立即上交任务单，教师根据学生完成情况进行赋分，占比20%。二是学生交流汇报情况。一般在游学结束一周后，教师组织学生以游学小组为单位进行PPT汇报展示，依照主题、内容、形式、表达四个方面进行赋分，占比20%（见表2）。

“六和塔”游学课程汇报展示评价表

[评价项目 关键评估点 赋分 优秀 良好 一般 主题 主题与游学课程实践高度相关，能体现数学学科特色 5 4 3 内容 内容原创，且丰富多彩 5 4 3 形式 形式新颖有特色，图文并茂，能吸引人 5 4 3 表达 语言表达清晰，能提出独到的见解 5 4 3 ]

“游在杭州学数学”整合性课程的终极目标是学生能够综合运用所学知识解决一些简单的实际问题，并由此产生学习动力与兴趣，为学生拓展了学习空间。学生在游玩的过程中参与社会实践，经历收集信息、处理数据、解决问题、与人合作交往的过程，使数学课变得更生动、开放、和谐，充满人文情怀。这种学习方式的转变，来自数学课程的改革，来自对数学本质的理解和感悟，并已然成为数学课程改革一道亮丽的风景线。

（浙江省杭州市萧山区教研室   311201）