基于自权值线性判别分析算法的图像处理研究

陆荣秀，蔡莹杰，朱建勇，杨 辉

（华东交通大学电气与自动化工程学院，江西 南昌330013）

在机器学习和模式识别领域中，降维是分析高维数据的一项重要方法。 在各类降维算法中，主成成分分析（principle component analysis，PCA）[1]和线性判别分析（linear discriminant analysis，LDA）[2]是运用最为广泛的两种降维算法。 其中，PCA 是一种无监督的算法，而LDA 则利用了样本的标签信息，是一种监督学习算法，LDA 的目标是学习一个映射矩阵使得类内散度最小化的同时最大化类间散度矩阵。 但是传统的LDA 仍然存在以下缺点：第一，当数据维度远远超过训练样本时，类内散度矩阵将会变成奇异矩阵，这会导致小样本问题[3-5]，所以传统的LDA 不适用于超高维的数据样本；第二，传统的LDA 假设输入的数据是符合高斯分布的，但是现实世界中的真实数据往往是呈多模态的非高斯分布[6-8]，传统LDA 算法往往在处理非高斯分布的数据时不能够很好地捕捉到隐含在数据内部的局部流形结构，导致降维效果不佳。

而对于非高斯分布的多模态数据，要从高维空间映射到低维空间中且不丢失原始数据的信息，最重要的是保证数据在从高维空间嵌入到低维空间的过程中能够保留数据的局部流形结构。 为此，许多科研工作者做了很多算法研究，其中最具有代表性的算法就是局部保持映射（locality preserving projection，LPP）[9]，该算法是让在原始空间中邻近成对的样本点在嵌入到低维子空间时样本点之间尽可能相互靠近，考虑了样本之间的相似性，从而使得非高斯分布的数据在映射到低维的子空间的过程中能够保留隐含在数据内部的局部流形结构。但是LPP 是一种无监督的学习算法，没有利用数据的标签信息，在一定程度上限制了其降维的性能。

基于以上的分析，本文提出了一种改进的线性判别分析算法，该算法在传统的LDA 的基础上，通过分析传统的LDA 算法不同形式的目标函数，利用样本对之间在数据空间里的距离分布，提出了一种自权值线性判别分析算法。 算法的主要思想是通过将输入数据在原始空间中的距离分布转换成其对应样本点之间的权值，对样本点之间的相似性与差异性进行区分，以保留隐含在数据内部的局部流形结构，从而改变了传统LDA 赋予样本相同权值的形式，也就是说，在改进的自权值LDA 算法中，当两个样本在原始空间的距离相近时，则样本对之间会被赋予较大的权值，这表明其在原始空间中的相似度越大，反之则赋予较小的权值，表明相似度越小。 从而使得数据从高维空间映射到低维子空间的过程中能够考虑样本点之间的差异性，抽取更多的数据局部结构信息， 发现数据内部中隐含的局部流形结构。 通过对传统的LDA 和改进的自权值LDA 算法在人工合成数据和真实数据上的实验对比分析， 结果表明改进的自权值LDA 算法相比于比于传统的LDA 算法，改进的自权值LDA 能够在一定程度上提高模型对非高斯分布的。

1 线性判别分析

线性判别分析算法是机器学习和模式识别领域广泛应用的降维方法， 其有效利用了样本的标签信息，属于有监督的学习算法。 本节将归纳总结传统线性判别分析算法的模型以及其对应的常规求解方法。

1.1 传统的LDA

给定一个数据矩阵X=[x1，x2，…，xl]∈Rd×l，LDA 的目的是学习一个线性转换矩阵，通过转换矩阵W∈Rd×m将d 维的数据xj映射到m 维子空间yj∈Rm（d＞m），使得样本点在低维空间中同类样本之间相互靠近，不同类之间的样本点相互远离。 数据映射关系表达式如下

式中：xj表示第j 个样本， LDA 假设最优的转换矩阵应该最小化类内散度的同时最大化类间散度。因此不失一般性，传统的LDA 的目标函数如下所示

式中：类内散度矩阵Sw以及总的散度矩阵St定义为

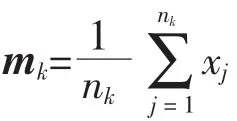
在目标函数式（2）中，为了确保解的唯一性，通常会对LDA 施加正交限制，则式（2）中施加了正交限制的LDA 目标函数为

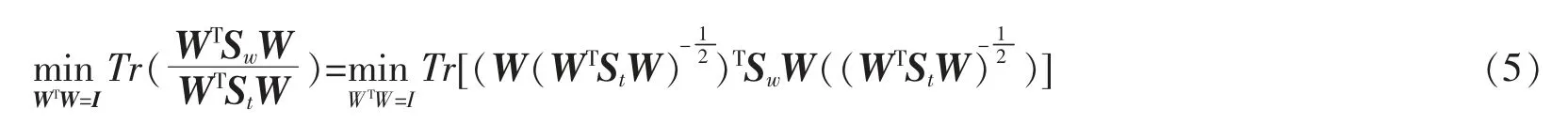
将式（5）写成向量形式

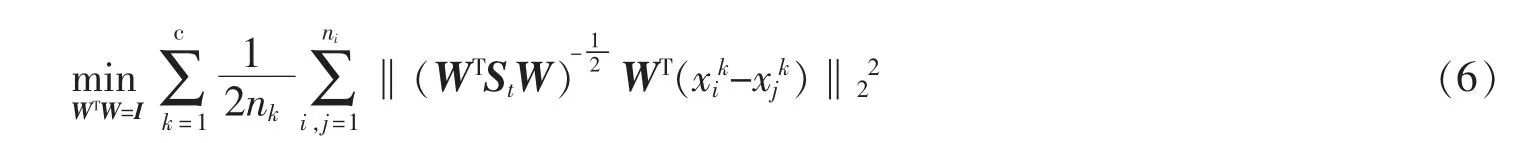
对于比迹形式的LDA 目标函数，式（5）通常可以通过广义特征值分解（generalized eigenvalue decomposition，GEVD）[10]进 行 求解，最优的转换矩阵W 可以通过进行以下的特征值分解得到

则最优的转换矩阵W 由St-1Sw中k 个最小的特征值所对于的特征向量组成，即W=[w1，w2，…，wk]。

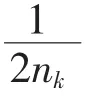
2 改进的自权值LDA 算法

在模式识别领域中，越来越多的降维技术被运用于图片处理领域[11-15]，例如人脸图片，医学影像图片[16]等。 LDA 是目前应用最广泛的图片降维技术之一，但是传统的LDA 只适合于处理高斯分布的数据，也就是说传统的LDA 是赋予类内样本点相同的权值，这使得LDA 让相互远离的成对的样本点相互靠近，因此传统的LDA 对处理高斯分布的数据具有很好的效果。

但是对于非高斯分布的数据，传统的LDA 则难以发现隐含在数据内部的流形结构，从而导致降维效果不佳。 这主要是因为传统的LDA 算法在数据点从高维空间嵌入到低维空间的过程中没有考虑样本间的相似性和差异性，最终使学习的映射矩阵不能完全辨识样本之间的判别信息。 因此本文针对传统的LDA 无法辨识样本对之间的相似性与差异性的问题，通过将样本对之间的距离分布转换为样本对之间的权值，以区分样本对之间的差异性,基于以上的分析并结合式（6），本文改进的自权值LDA 的目标函数定义如下

2.1 目标函数的求解

在上一节中，本文通过在传统的LDA 模型的基础上，改进了其不能区分样本点之间差异性的问题并定义了基于自权值的LDA 目标函数。 这一节，本文将介绍对改进的自权值LDA 模型的求解过程。

首先在求解式（9）时，先计算样本之间的权值系数，同类样本之间的权值系数为pijk，不同类的样本的权值设置为0，所以当权值系数已知时，基于自权值LDA 算法的总的散度矩阵S~t和类内散度S~w定义为

根据式（11），式（9）可以进一步写成其矩阵的形式

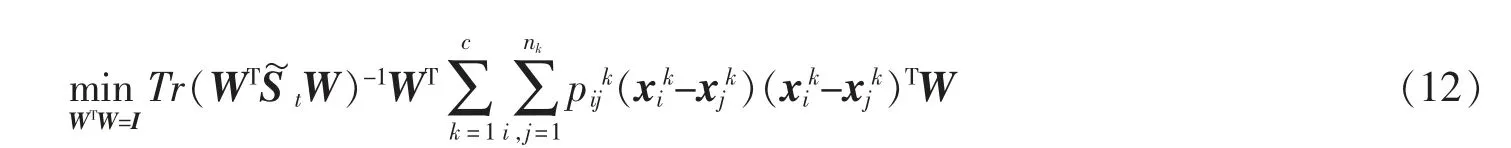
其中Tr（·）表示矩阵的迹，式（12）可以进一步化简为

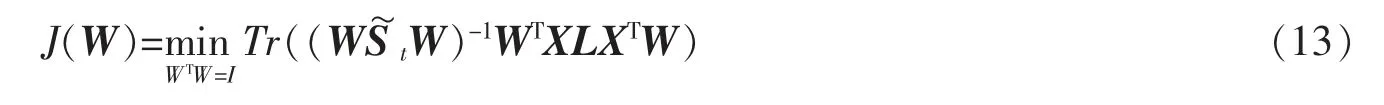
其中

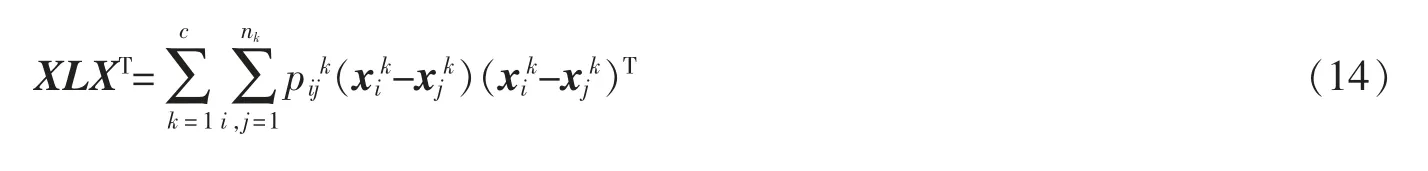
式中：L=D-A 为拉普拉斯矩阵， 其中A 为对称矩阵，D 为对角矩阵，D 的对角元素为对应A 的每列列和，A表达式如下：

其中πk表示第k 类样本，权值系数pijk可由样本点计算得到，则根据式（5），最终式（13）中的映射矩阵可以通过求解以下的广义特征值问题得到

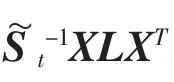
输入：数据矩阵X∈Rd×n，标签：y∈Rm降维的维数为m。

1） 计算样本对之间的权值系数pijk；

3 实验

3.1 实验设置

为了有效的分析改进的自权值算法的降维性能，设置的实验主要由三部分组成，第一部分主要是针对于人工数据，用随机生成的符合高斯分布的数据和非高斯分布的数据，来可视化检验传统的LDA 以及改进的自权值LDA 的降维效果。 第二部分主要为常见的UCI 数据集， 对比的算法分别是相关传统的降维算法LDA 和LPP ；第三部分实验主要为人脸图片，对比的算法为传统的LDA 算法。 实验中我们随机从每个类中选择相同比例的样本用作训练集，其余的样本用于测试集，训练集的比例设置为0.5。 另外，采用PCA 预处理以保留所有数据的95% 信息以便删除数据协方差矩阵的零空间。 实验中， 使用k 最近邻 （k-Nearest-Neighbor，kNN）（k=1）分类器对样本进行预测分类。 每次实验随机分割数据集进行预测，分别进行20 次。 不同算法在不同维度的预测正确率如图2 所示，在所有的降维维度中，预测的最好的平均正确率的维度及其标准偏差如表4 和表5 所示。

3.2 数据集描述

3.2.1 实验二数据集介绍

实验二选取了6 个数据集， 在表2 中给出， 分别是：Control，Segment，Dermatology，Letter，Mnist，USPS。Dermatology 为皮肤病学数据集，这个数据库包含34 个属性，其中33 个是线性值，一个是标称值。Mnist 标准的手写数字数据库,它包含3 495 张手写数字图片共10 类，每张图片的为784 个像素点。 USPS 是美国邮政USPS 的手写数据集，它包含9 298 张手写数字图片共10 类，每张图片的大小为16×16 个像素点。 关于不同数据集的具体描述如表1 所示。

表1 UCI 数据集描述Tab.1 UCI data set description

3.2.2 实验三人脸数据集介绍

实验三的人脸数据集在表4 中给出, 分别是AR， FERET， MSRA25， ORL，Umist，YaleFace。各个数据集的简短介绍如下：

AR 数据集包含超过4 000 张彩色图像，对应126 张人脸，图像具有不同面部表情、照明条件和遮挡的正面视图脸。 FERE 是一个标准的面部图像数据库，它共收集了14 126 张图像，涉及1 199 个人。 它包含20类共574 张人脸图片，每张图片的像素点10 304 个像素点。MSRA25 包含12 个受试者的1 799 张脸部灰度图片，每一类中有113～186 张不同姿势的照片。每张图片的像素点是16×16 像素。ORL 共包含40 个不同人的400 张图像。 每张图片的像素点是32×32 像素。 Umist 人脸数据库由564 张20 人的图像组成。 每个人都以从侧面到正面的一系列姿势。YaleFace 人脸数据库包含165 张15 人的GIF 格式灰度图像。每个受试者有11 个图像。 关于不同数据集的具体描述如表2 所示。

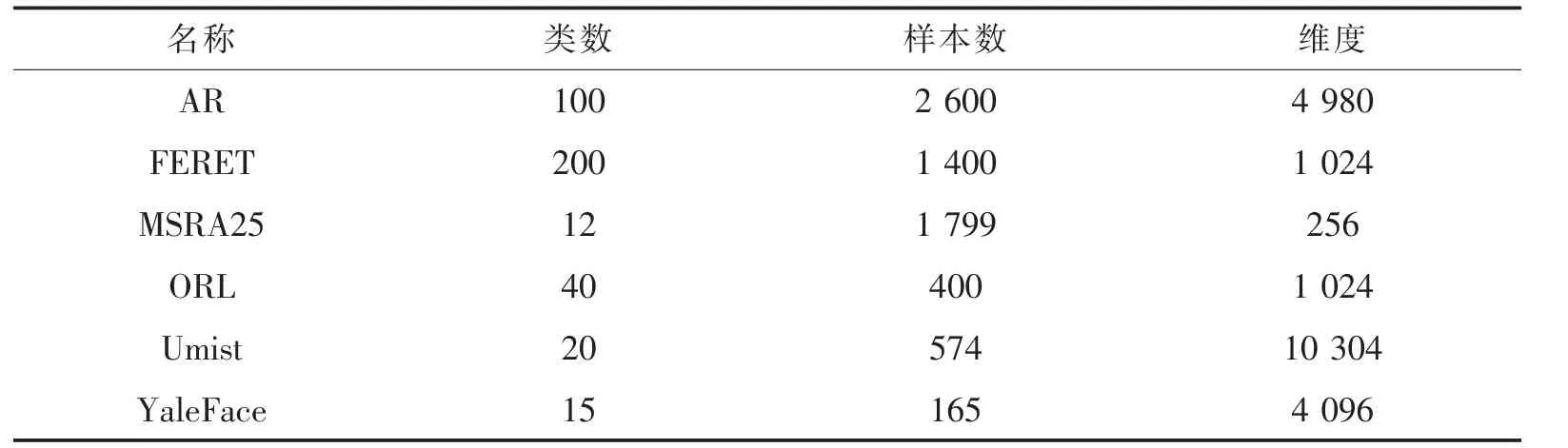
表2 人脸数据集描述Tab.2 Face data set description

3.3 实验结果与分析

为了体现提出的算法的有效性,本文分别用人工数据，常规的UCI 数据集以及人脸数据集分别对模型性能进行评估，在实验中本文对比了3 种相关的降维算法，分别是LDA，LPP。其中LDA 是监督的降维算法，LPP 是无监督的降维算法。

在实验结果中，人工数据实验的结果如图1 所示，图1 中虚线代表的是LDA 求解的投影方向，实线代表的是改进的算法求解的投影方向。 图1（a）中的数据为人工随机生成的高斯分布数据，图1（b）中的数据则是非高斯分布的人工数据。从图中可以看出，对于高斯分布的数据，LDA 和改进的新算法所学习的映射方向基本一致，而对于处理非高斯分布的数据， LDA 学习的投影方向会出现许多样本的重叠，这说明加入了自权值后得新算法相比于传统的LDA 很好的保留了数据局部的几何结构。

UCI 数据实验结果如表3，图2 所示，在图2 中，轴表示降维的维度，x 轴为分类的正确率，分类器为k最近邻（kNN）（k=1）分类器。OUR 代表的是改进的算法，LDA，LPP 为相关的对比算法。 实验的数据集如表3所示，每种算法在不同的数据集中最好的分类正确率以及标准差如表2 所示，在不同的降维维度不同算法的正确率如图2 所示。

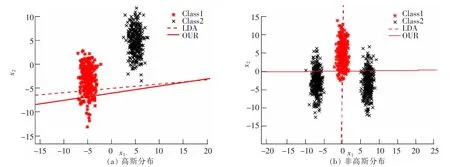
图1 改进的LDA 与传统LDA 在高斯分布与非高斯分布的人工数据上学习投影效果Fig.1 The proposed LDA and the traditional LDA learning projection results on the artificial data of Gaussian distribution and non-Gaussian distribution

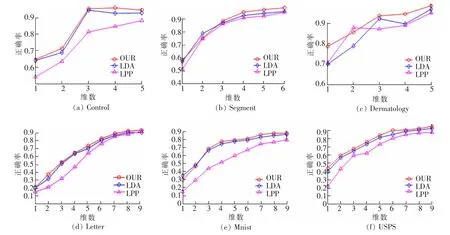
图2 UCI 数据在不同对比算法中不同降维维度上的平均正确率Fig.2 Average accuracy of UCI data with different dimension reduction in different comparison algorithms

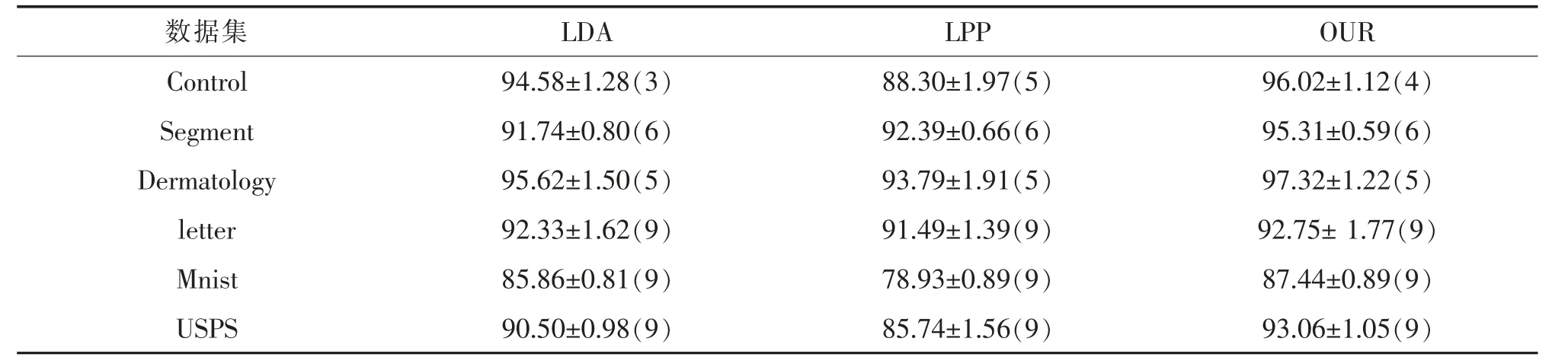
表3 UCI 数据集识别的平均正确率(均值±标准差)，最好的预测结果用黑体加粗Tab.3 The average accuracy of UCI dataset identification (mean ± standard deviation (reduction dimension), and the best prediction results in bold

人脸图片数据实验结果如表4 所示， OUR 代表的是改进的线性判别分析算法， LDA 代表的是传统的线性判别分析算法。baseline 表示的是没有经过降维处理所分类的正确率。实验中所用的人脸数据集在表3中给出。 从以上的实验结果中，本文可以得出以下结论：

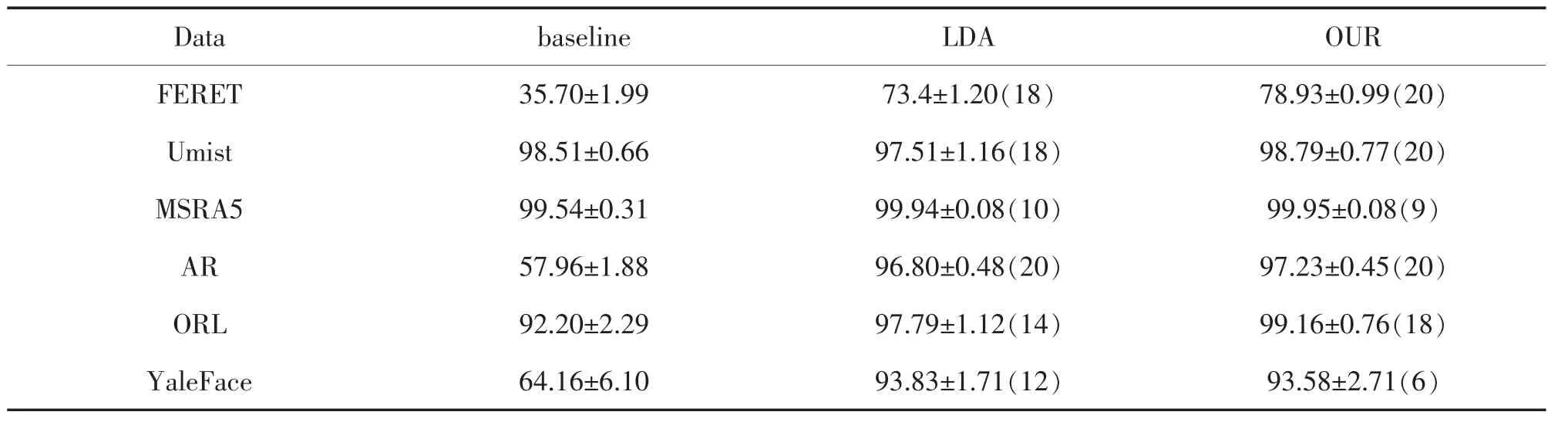
表4 人脸数据集识别的平均正确率（均值±标准差（降维维度）），最好的预测结果用黑体加粗Tab.4 The average accuracy ofFace dataset identification （mean ± standard deviation （reduction dimension）），and the best prediction results in bold

1） 从图1 中的人工数据实验可以看出，对于高斯分布的数据， LDA 和新算法都能有较好的表现，而对于处理非高斯分布的数据，传统的LDA 表现性能不佳，学习的映射方向经过样本点的投影后出现了许多样本点的重叠，而新算法则很好的保留了数据的局部几何结构,体现了改进的自权值LDA 算法对非高斯数据的处理能力。

2） 从表4 中可以看出，改进的线性判别分析算法的预测最佳正确率均高于传统的降维算法，这表明改进的算法在加入了自权值的特性后，能够抽取样本点之间更多的判别信息，提高了降维性能。

3） 从图2 中可以看出，对于Mnist 数据集，改进的算法与LPP 的表现整体好于传统的LDA 算法，这表明相比于传统的LDA 算法， 改进的线性判别分析算法和LPP 都能够通过区分样本间的相似性与差异性提高降维性能，而对于Control, Mnist, USPS 数据集等，改进的算法和LDA 的表现则整体好于LPP，这是因为LPP 是无监督的学习算法，它没有利用标签信息，而改进的新算法则是附带有权值的监督学习算法，充分的利用了样本的标签信息，因此整体的表现性能更好。

4） 从表4 中可以看出，在6 个人脸数据集中，改进的模型只有在YaleFace 的数据集上的分类正确率略低于传统的LDA，在其他人脸数据集上，改进的模型的预测分类正确率均优于传统LDA。这表明改进的新算法由于考虑了样本之间的相似性与差异性，从而使得新模型能够在样本点从高维空间嵌入到低维空间的过程中考虑隐含在数据内部的流形结构，因此整体性能得到改善。

4 结论

本文针对传统的线性判别分析（LDA）算法未考虑数据从高维空间嵌入到低维空间中的局部流形结构，在处理非高斯分布数据时不能取得较好效果的问题，提出了一种新的监督降维的算法，利用数据在原始空间的距离分布，将样本间的距离分布大小转换为样本对之间的权值来用作区分样本间的差异性，从而使得数据从高维空间映射到低维空间中能够保留数据中的局部几何结构， 使得新的模型相比传统LDA 算法不仅适用高斯分布的数据，同样也适用于非高斯分布的数据。 大量的实验表明改进的新算法相比于传统的线性判别分析算法能够更好的抽取数据局部的流形结构，也充分验证了新算法的有效性。