基于骨料形态的细观混凝土建模与裂缝研究

周瑜亮，金 浩

（1.同济大学道路与交通工程教育部重点实验室，上海201804；2.上海市轨道交通结构耐久与系统安全重点实验室，上海201804）

目前，大多数针对混凝土工程结构的力学研究中，将混凝土材料看作均质连续介质，假设为各项同性材料[1-2]。然而，真实的混凝土由骨料、砂浆、细砂等材料组成，宏观模型不能解释混凝土材料内部结构的相互作用以及宏观裂缝的扩展规律。 细观数值仿真的提出解决了宏观层面材料均质化而难以表述其随机性的难题，同时避免了微观层面的海量计算，对混凝土材料破坏的影响及细观裂缝发展与宏观力学性能之间的关系提供了新思路。

作为混凝土细观模型的核心问题，骨料形状的模拟直接影响着混凝土的强度、裂缝开展等宏观特性。学者针对骨料形状的模拟做了不同的尝试。 早期的骨料模型普遍采用规则几何模拟，如采用圆形[3-5]或者椭圆[6-7]模拟卵石骨料，对于形状较为复杂的碎石骨料，高政国等[8-10]利用简单平面几何和立体几何，将边或面延向其法向方向向外随机延拓，形成多边形（多面体）的混凝土骨料；Zhang 等[11]、徐乐等[12]基于维诺泰森多边形方法，在空间中生成任意随机点，通过随机点间距离中垂线将空间切割成多面体形成骨料颗粒；宋来忠等[13-14]基于参数曲面的自由变形技术，定义伸缩因子，用确定的、形式统一的参数方程将骨料予以表示。随着CT 扫描、X 射线等先进技术的引入，部分学者从实际试件中获取真实骨料的参数信息。 于庆磊等[15-18]利用CT 扫描和数字图像处理技术获得了真实试件截面上骨料的形状、位置、孔洞等信息，重构了与试件截面相一致的细观模型；Ren 等[19-20]通过CT 扫描得到一系列二维图像，利用体数据场重建了三维混凝土细观模型试件。

上述骨料模拟的方法中，前一类规则几何骨料与真实骨料形貌上差异较大，后一类骨料受采样试件的级配限制，模拟不规则结构时有所困难。为解决上述问题，通过对碎石骨料的图像处理获得单个骨料的轮廓形状，并将轮廓点进行随机移动，形成真实骨料的随机生长。针对碎石骨料复杂的几何边界，提出“先投放多边形-后投放外接圆”的侵入判别准则，实现骨料的快速投放。 通过建立混凝土梁三点弯曲数值模拟分析骨料形状对裂缝扩展的影响。

1 细观混凝土建模

1.1 基于图像处理的骨料几何生成

骨料形态的模拟是混凝土细观模型的基础。 基于单个真实骨料图像处理及轮廓控制点处理对骨料形态进行建模。 首先，利用激光扫描仪对单个骨料进行扫描，得到骨料的三维图像，在此基础上对骨料进行随机旋转得到不同视角的骨料截面。 将骨料图像导入MATLAB 中， 采用内置的二值化函数im2bw 和膨胀函数imdilate 对图像进行处理。最后，利用bwperim 和bwboundaries 函数提取骨料的有序轮廓控制点坐标。 随后，为优化控制点数量，采用曲率及两点间最小距离控制来减少轮廓控制点。 其中，曲率控制采用“三点法”，控制条件为相邻3 个几何点构成的三角形外接圆曲率半径小于某一给定值；两点间最小距离控制时，首先计算骨料的平均粒径，并假定轮廓上任一点为起始点，计算相邻2 个控制点之间的距离满足

式中：Rave为骨料平均粒径；Ri为轮廓控制点至几何中心的距离；N 为轮廓控制点个数；α 为距离控制系数。简化后的骨料形状可以由几何控制点及直线生成，如图1 所示。

图1 真实骨料图像处理Fig.1 Actual aggregate image processing

图2 控制点随机移动生成新骨料Fig.2 Random movement of control points

1.2 骨料投放及侵入判断

骨料的投放采用“先投放多边形-后投放外接圆”侵入判断的骨料投放算法。新骨料投放时，只要将其外接圆投放至指定区域内即可完成该个骨料的投放，在投放时需判断既有骨料边界轮廓与新骨料外接圆是否重叠，即可理解为多边形与圆的侵入关系，此外，骨料是按照从大到小进行投放的，避免了由于外接圆与骨料之间存在空隙导致的骨料含量偏低的问题。 在判断圆与多边形的位置关系时，可分为控制点在圆内部、控制点连线与圆相交和圆在多边形内部3 种情况，如图3 所示。 对于第1 种情况，直接判断骨料控制点是否在外接圆内部即可；对于第2 种情况，判断外接圆圆心与相邻控制点直线方程的距离是否小于半径且垂点是否落在控制点形成的线段上；对于第3 种情况，判断通过外接圆圆心与各轮廓控制点的夹角之和是否等于360°。该算法中，3 种判断是按顺序进行的，一旦前者条件不满足，后续条件无需计算直接进入下一个骨料的判断。

与传统算法相比，由于其不需要检测特殊相交情况，即新投放骨料的顶点不在既有骨料内部，但两者骨料边相交的情况[9]；因此大幅减少了判断变量的计算次数。 不同侵入判断准则的对比如表1 所示，其中n 为单个骨料的边数。

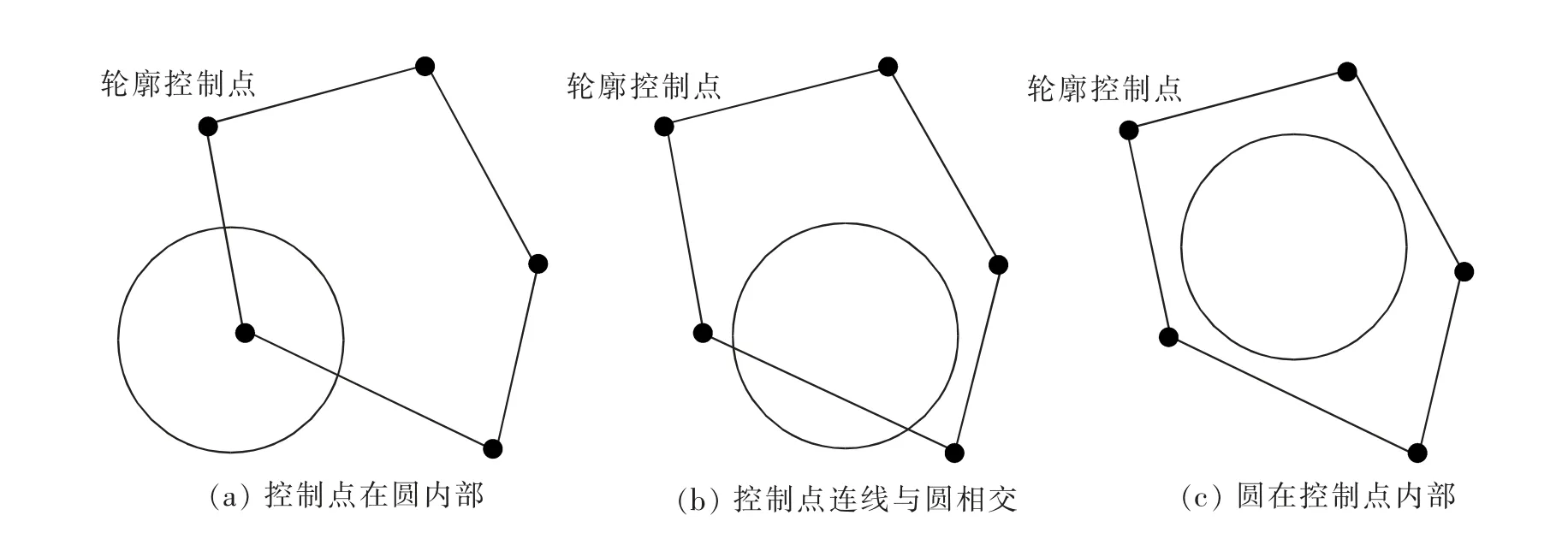
图3 外接圆与多边形侵入判断Fig.3 Polygons-circumcircle conflict and overlap criteria

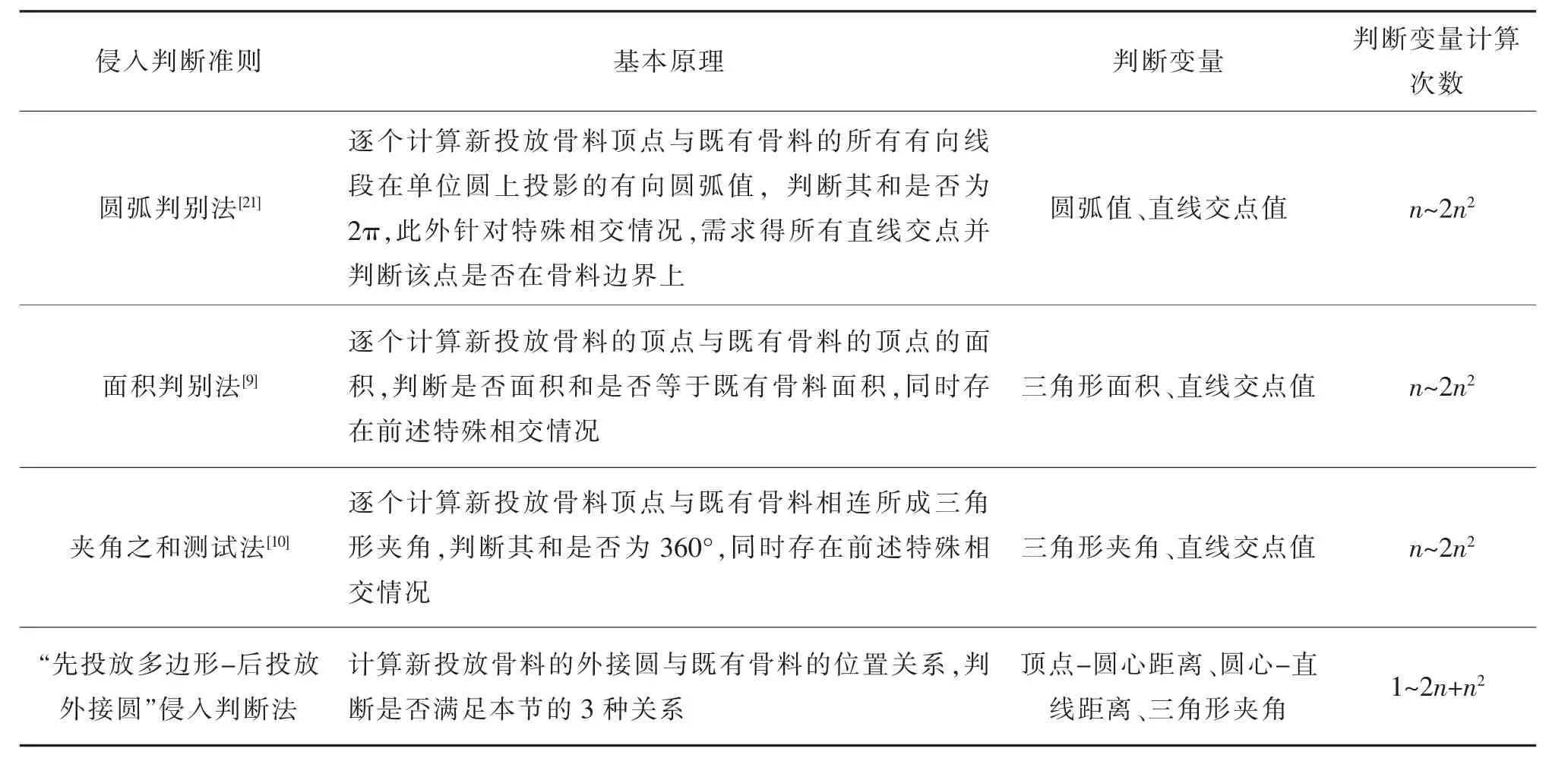
表1 侵入判断准则对比Tab.1 Comparison of intrusion criteria

混凝土的粗骨料按粒径和分为小石（5～20 mm）、中石（20～40 mm）、大石（40～80 mm）以及特大石（80～150 mm），按包含粒径范围分为一、二、三、四级配。采用上述方法分别生成二、三、四级配的混凝土试块，进行轮廓点随机移动后，为使骨料之后能够按照骨料级配进行随机投放，需对骨料进行“骨料旋转化”和“粒径级配化”处理。 “骨料旋转化”即将选定的骨料绕其外接圆中心进行随机旋转

式中：x0，y0为旋转前的控制点坐标；x1，y1为旋转后的控制点坐标；ran1，ran2 为0 到1 的随机数。

“粒径级配化”是根据骨料投放的级配范围，在范围内对骨料进行随机扩放，生成满足级配要求的骨料：

式中：x1，y1为扩放后控制点坐标；D1，D2分别为该级配范围内的最大和最小粒径，ran3 是0 到1 的随机数。

投放前，利用瓦尔文公式计算各级配所占区域的面积，瓦尔文公式[22]如下

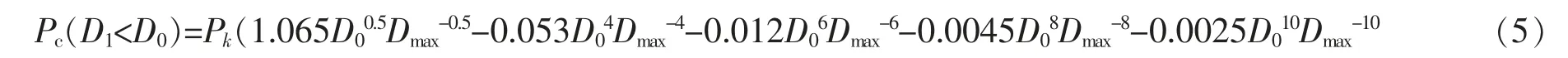
式中：Pc为粒径D 小于D0的概率；D0为所计算概率范围内的最大粒径值；Dmax为最大粒径；S 为投放区域面积；Si为第i 级配的面积；Pci1，Pci2分别为第i 级配下粒径的上下限。 在生成级配粒径范围内随机生成骨料直至达到骨料面积，确定各骨料外接圆后从大到小进行排序。 利用上述算法根据骨料级配从大到小逐级进行骨料投放。生成的试件如图4所示， 其中二级配骨料模型尺寸为150 mm×150 mm，骨料含量达55.42%；三级配骨料模型尺寸为300 mm×300 mm，骨料含量达62.17%，四级配骨料模型尺寸为450 mm×450 mm， 骨料含量达64.00%。

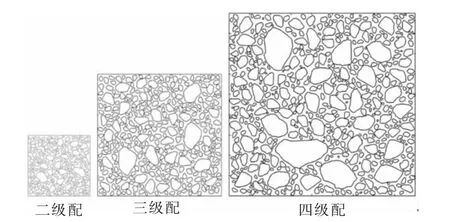
图4 随机骨料投放样例Fig.4 Random aggregate placement sample

2 三点弯曲梁数值试验

2.1 模型建立

为研究骨料形状对裂缝路径扩展及宏观力学性能的影响，选取了不同椭圆度的骨料，即骨料等效椭圆长轴与短轴之比， 分别生成3 组试件， 如图5 所示， 骨料含量均在42%左右， 椭圆度分别为1.63，1.98 和2.42。 在此基础上进行无缺口三点弯曲梁试验，以便观察裂缝的形成过程以及骨料形状的影响，试件尺寸取400 mm×100 mm，由于裂缝多在梁中部发生，为提高模型的计算效率，将中间100 mm 设置为非均匀模拟区，其余区域设置为均质材料，梁计算简图如图5 所示。

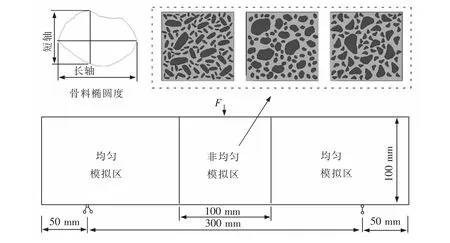
图5 三点弯曲梁细观模型Fig.5 Meso-scale model of a three-point curved beam

2.2 混凝土细观本构

采用ABAQUS 中损伤塑性模型（concrete damage plastic model）描述混凝土各相材料的断裂行为，该模型可通过各相同性弹性损伤结合各相同性拉伸和压缩塑性理论来表征混凝土的非弹性行为。 在混凝土试件的数值计算中，若本构模型采用应力-应变关系，计算结果一定程度上受计算网格大小的影响，引起数值结果的网格依赖性[23]。 因此，材料的开裂行为采用Petersson[24]提出的双线性软化曲线，裂缝面上传递的拉应力大小决定于它的张开度ω，即σ=σ（ω），并通过控制材料的断裂能以保证裂缝开展时所需的能量是唯一的。只需抗拉强度ft和断裂能Gf两个参数即可确定材料的软化关系，对于参数取值，Petersson 建议采用σs=ft/3，ωs=0.8Gf/ft和ω0=3.6Gf/ft。 材料的压缩行为采用双折线损伤变量演化模型[25]，根据文献中的定义，计算中λ取0.1，ζ 取10，骨料，砂浆和界面的η 分别取5，4 和4，并且参考文献中对材料参数的取值，并通过数值试验进行参数反演，得到的各相材料力学参数取值见表2。

表2 各相材料力学参数[8-9]Tab.2 Material mechanical parameters of each phase

2.3 模型有效性验证

选取petersson 所做的三点缺口弯曲梁试验进行对比试验。 梁的几何尺寸为2 000 mm×200 mm×50 m，缺口尺寸为40 mm×100 mm。采用上述提出的骨料生成方法生成3 组试件SJ1，SJ2，SJ3，骨料粒径范围为5～40 mm。 图6 所示为模拟的3 组试件试验的荷载-挠度曲线， 可知模拟结果与试验结果符合良好。 数值模拟结果的曲线峰值与试验测试的极限荷载基本一致。 然而，由于残余应力的积累，可以观察到软化曲线末端的模拟和试验之间的有所差异。 模拟结果和试验结果的一致性表明，所提出的基于真实骨料的细观数值模型和所采用的非线性本构模型可以用来模拟非均质混凝土的断裂。

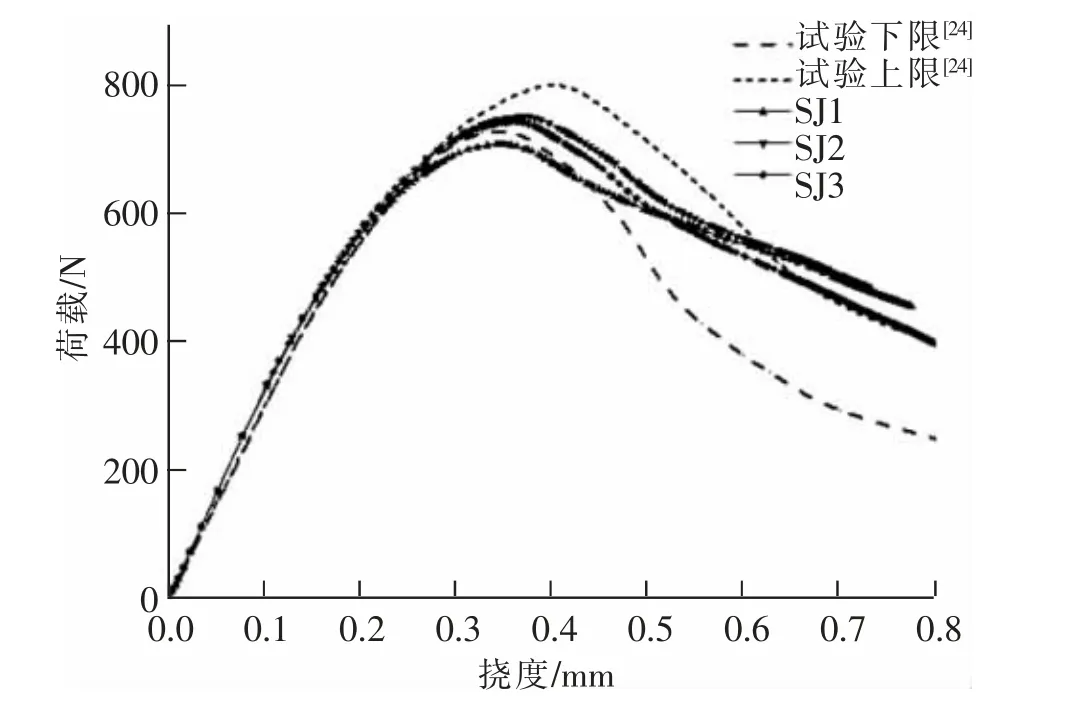
图6 荷载-挠度曲线Fig.6 Load-deflection curve

2.3 数值结果与讨论

以GL1 试件为例，分析荷载-挠度曲线与裂缝发展过程，如图7（a）所示，在弹性阶段荷载挠度基本按线性比例变化，且各组结果基本重合，在这个过程中试件的应变分布较为均匀；随后在试件底部附近出现了弥散裂纹，应变分布不再均匀并向中部集中，由于挠度的增长大于荷载的增长，荷载-挠度曲线变凸，非线性特征逐渐明显；在图7（a）中峰值点前后f≥0.9 fpeak范围内，弥散裂纹逐渐转化为局部集中裂纹，之后随着挠度的不断增大，局部化效应更加明显，裂纹不断向上扩展贯通，最终形成宏观裂缝并导致试件失稳破坏。

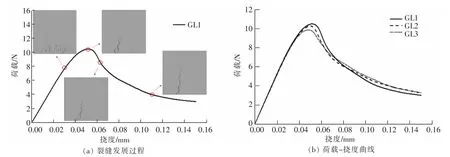
图7 无缺口三点弯曲梁模拟结果Fig.7 Simulation results of three-point bending beam without notch

根据数值试验结果得到荷载-挠度曲线如图7（b）所示，3 组试件的曲线弹性段基本一致，非线性段各组试件差异逐渐凸显。 其中，混凝土内部骨料椭圆度越小，曲线的荷载峰值越大，但在软化段荷载值下降更快，即骨料的椭圆度与极限强度成反相关，与残余强度成正相关。 选取梁中部的最大主应变大于2×10-6的应变作为可见裂缝，对各组数据进行归一化处理并进行分析，以便观察骨料形状对裂缝走向的影响。 图8 所示为梁中部挠度分别为0.03，0.04，0.05 mm 和0.06 mm 时3 组试件的最大主应变场。 GL1 试件微裂缝萌生后裂缝较均匀开展，并逐渐向受荷点集中。 这是由于骨料的椭圆度更小，骨料各边的方向及边长长度分布概率相近，裂缝能绕过骨料按原路径发展，最终裂缝路径的方向指向加载点；GL2 试件和GL3 试件初期微裂纹萌生与GL1 试件类似，但由于骨料的椭圆度更大，裂缝扩展时，骨料几何较长的边对裂缝走向有较强的导向和阻裂效应，特别是对于粒径较大的骨料，长边效应更为明显，GL2 试件和GL3 试件的最终裂缝路径偏离了加载点，进而导致曲线的软化性段下降速率变慢。 据上述分析可知，在相同荷载条件下，混凝土内部的骨料椭圆度越小，对裂缝的导向和阻裂效应越弱，反之越强。

图8 梁中部最大主应变场（归一化）及最终宏观裂缝Fig.8 Maximum principal strain and ultimate macroscopic crack in the middle of the beam

3 结论

提出一种基于真实骨料形态的二维混凝土细观建模方法。 利用图像处理获取真实骨料的几何轮廓，通过骨料轮廓点在平面中的随机移动，形成真实骨料的随机生长。 建立“先投放多边形-后投放外接圆”的骨料侵入判别方法。通过三点弯曲梁数值模拟，分析骨料椭圆度对裂缝路径扩展和宏观性能的影响，得到如下结论：

1） 本文建模方法相较于传统的细观混凝土建模方法，生成的骨料形状源于真实骨料，形态上更接近真实骨料，能够更精确模拟裂缝的扩展。

2） 针对骨料形状的复杂性，提出“先投放多边形-后投放外接圆”的骨料侵入判别方法，该方法简化了复杂多边形侵入判别的过程。

3） 当梁受弯后，在梁跨中底部附近出现了弥散裂纹，随着挠度的增长，弥散裂纹逐渐转化为局部集中裂纹，紧接着局部化效应更加明显，裂纹不断向上扩展贯通，最终形成宏观裂缝并导致试件失稳破坏。

4） 试件中骨料形状不同导致裂缝和宏观强度也不同。 骨料椭圆度越大，梁的抗弯极限强度越小，残余强度越大，对裂缝走向的导向和阻裂效应越明显，大粒径骨料的长边效应更显著。