优化问题结构 引领深度学习
——《多边形的内角和》教学
2020-07-08
【教学内容】
苏教版四年级下册第96、97页。
【核心问题】
多边形的内角和与边数有什么关系?
【教学准备】
课件、各种多边形。
【教学过程】
一、设疑引入,激活思维
1.复习回顾。
师:回忆一下,在前面的学习中,我们认识了哪些多边形?
生:我们认识的多边形有长方形、正方形、三角形、平行四边形和梯形。
生:还有五边形和六边形等等。
师:(出示三角形)我们已经掌握了三角形的哪些知识?
生:我知道三角形有三条边、三个角。
生:三角形的内角和是180°。
2.设疑引入。
师:(出示十二边形)这是一个十二边形,你知道这个十二边形的内角和是多少度吗?看来有点困难,遇到这样复杂的问题,可以怎么办呢?
生:可以从简单想起。
师:今天我们就一起研究多边形的内角和。(揭示课题)我们从几边形开始研究呢?
生:四边形。
二、小组“合学”,有序探究
1.引发猜想。
师:长方形和正方形都是四边形,它们的内角和是多少度?
生:长方形和正方形四个角都是直角,所以内角和是90°×4=360°。
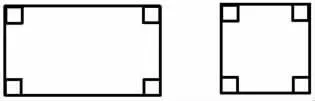
师:根据这一特点,你能作出大胆的猜想吗?
生:我猜想“所有四边形的内角和都是360°”。
2.“合学”研究。
师:是不是所有四边形的内角和都是360°呢?需要动手验证一下。老师为每组准备了不同的四边形,想想如何验证?再动手试一试。
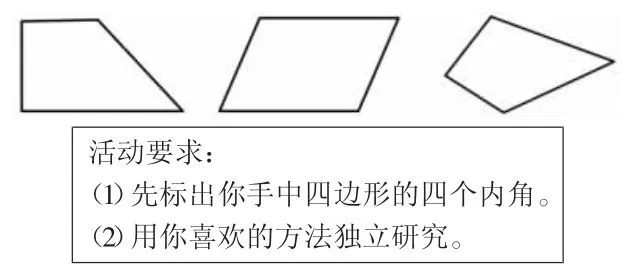
师:哪位同学愿意先来汇报你们组的研究结果?
生:我们组研究的是梯形,我先将梯形四个内角标出来,然后将它们撕下再拼在一起(如图1),正好是一个周角,所以这个梯形的内角和是360°。
生:我是将梯形分成两个三角形(如图2),一个三角形的内角和是180°,两个三角形就是180°×2=360°。

图1
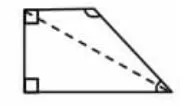
图2
追问:为什么要将四边形分成两个三角形呢?
生:因为我们已经知道三角形内角和是180°,将四边形分成两个三角形,就能算出四边形内角和的度数。
师:这位同学将四边形内角和的问题转化为三角形内角和的问题来解决很巧妙。(板书:转化)
生:我们组研究的是平行四边形(如图3),先用量角器量出四个角的度数,然后将它们相加:65°+115°+65°+115°=360°。
生:我们组研究的是这样的四边形(如图4),除了前面的方法,我还有一种方法,将这个四边形分成四个三角形,用180°×4=720°,然后减去中间的四个角,所以用720°-360°=360°。

图3
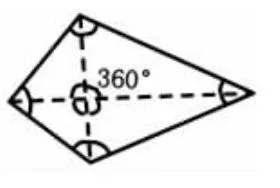
图4
生:我不太赞同你的想法,你将四边形分成四个三角形,如果将这四个三角形继续分,还会得到八个三角形,这样就把问题弄复杂了,我认为只要分成两个三角形就可以了。
3.比较归纳。
归纳:刚才大家用自己的方法研究了不同四边形的内角和,不管是量、拼还是分,发现四边形的内角和都是360°。
4.深入探索。
师:五边形的内角和你还能继续研究吗?
(学生动手操作,组内交流,然后组织反馈)
生:我把五边形分成三个三角形(如图5),每个三角形的内角和是180°,三个三角形的内角和就用180°×3=540°。
生:我将五边形分成一个三角形和一个四边形(如图6),用180°+360°可以算出五边形的内角和是540°。
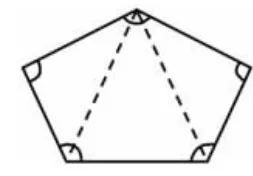
图5
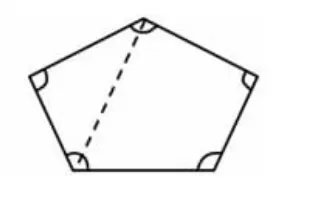
图6
生:我认为图5的方法就是将图6的方法中四边形再分成两个三角形。
生:我更喜欢图5的方法。把五边形分成一个三角形和一个四边形,如果边数再增加,出现的情况就很复杂了,所以不如都分成三角形反而显得简单。
师:老师也赞同你的想法,通过分割的方法把五边形转化成了三个三角形,根据三角形的内角和来计算五边形的内角和,这种方法比较简洁。
师:同学们在汇报时,很少有同学用量或拼的方法,为什么呢?
生:因为五边形的角太多了,撕开来再拼比较麻烦,五个角拼在一起,也不能知道是多少度。
生:如果用量的方法,既麻烦又不准确。
小结:研究五边形的内角和时,发现用分的方法比较简便,分成了三个三角形,得到五边形的内角和是540°。
师:那六、七、八边形……的内角和可能是多少度呢?你能想办法求一求吗?老师给大家准备了这几种图形,请每位同学挑选一种进行研究。
生:我研究的是六边形,六边形可以分成四个三角形,内角和是180°×4=720°。
生:我研究的是七边形,七边形可以分成五个三角形,内角和是180°×5=900°。
生:我研究的是八边形,八边形可以分成六个三角形,用180°×6=1080°。
师:现在你能解决课前提出的“十二边形的内角和是多少度”这个问题了吗?
生:12-2=10,180°×10=1800°。
师:你是怎么想到用12减2的?
生:其实这是有规律的……
三、总结规律,聚焦明理
1.总结规律。
师:刚才说其中是有规律的,是什么规律呢?
生:我发现分成三角形的个数可以用边数减2。求多边形的内角和,我们可以用(边数-2)×180°。
师:同学们真棒!知道这个规律后,你还能求出多少边形的内角和?
2.聚焦明理。
师:你知道为什么三角形的个数比边数少2 吗?仔细思考,相信大家一定会有新的发现。
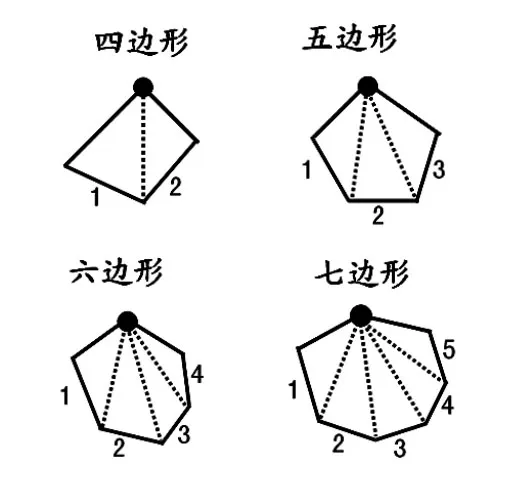
生:我发现有几条对边就能分出几个三角形。
生:任何一个多边形的顶点都能和对边形成三角形,每个顶点都有两条边是相邻的,不能得到三角形,因此分出三角形的个数就比边数少2。
师:同学们真了不起,不仅能够自己探索和发现规律,还能悟出其中的道理。掌声送给自己!
四、总结回顾,结构反思
师:今天我们一起研究了多边形的内角和,大家回忆一下一开始我们遇到了什么问题?我们又是怎样解决的?
生:我们开始遇到求十二边形的内角和是多少度,遇到这样的复杂问题,我们从简单想起,从四边形内角和开始研究。
师:然后我们又研究了哪几种多边形,发现了什么规律?
生:我们接着研究了五边形、六边形、七边形和八边形的内角和,发现了“多边形的内角和=(边数-2)×180°”这一规律。
生:我们还明白了分成三角形的个数比边数少2的道理。
