一类改进DBSCAN算法及在金融中的应用
2020-07-07黄翰诚
黄翰诚, 江 渝
(上海财经大学数学学院,上海200433)
§1 引 言
随着中国市场交易规模的不断扩大,证券交易所需要重点监控并及时发现多个涉嫌关联的账户组成的信息群落间的交易一致性,查处其进行内幕交易,操纵市场价格的违法行为(参见[1]).信息群落的发现主要是利用各个基金的前十支重仓股的持股比例信息.如统计深圳交易所2017年第三季度2902个基金前十支重仓股,总共持有1577支不同股票,即组成了一个2902×1577的矩阵,行坐标代表基金,列坐标代表股票,矩阵的每个元素是持股百分比.由于只考虑持股比例前十的股票,矩阵会含有大量持股0%的零元素,就具有了数据量较大,稀疏且高维的特点.该矩阵的每个行向量,即每个基金的持股向量就是高维空间中的一个点.可以考虑运用聚类算法将具有关联性的数据点聚为一类,就能发现潜在的信息群落.
Sambasivam S指出不存在一种聚类算法可以普遍适用于各种多维数据集所呈现出来的多种多样的结构[2].常用的聚类算法有K-means算法[3],STING算法[4],DBSCAN(Density-Based Spatial Clustering of Application with Noise)算法[5],OPTICS算法[6],DENCLUE算法[7],COBWEB算法[8],CLASSI算法[9],AutoClass算法[10],AP聚类算法[11],CFSFDP算法[12]等.由于研究的数据集含有较多噪声,最终选择了基于密度的聚类算法DBSCAN算法,并针对该算法的缺点以及需要研究数据的特征改进了算法,将算法参数改为自适应参数,此外新定义了能够更好地刻画基金间相似程度的“距离”,增强了改进算法发现潜在的信息群落的能力.
本文的后续内容安排如下:§2主要介绍了DBSCAN算法,指出传统算法中半径参数ε敏感度高,对于多层密度数据集难以选择全局参数而导致聚类结果差等缺点.针对这个缺点,§3提出了具有自适应参数的改进算法.并基于实际数据特征,自定义了刻画两个基金间相似程度的综合距离,使得改进算法能更好地应用在解决实际问题上.§4通过基于模拟数据和实际数据的数值实验,验证了改进算法的有效性.
§2 DBSCAN算法
DBSCAN算法是一类基于密度的聚类算法.其主要思想是从数据集合X={x1,x2,...,xN}中任意一个数据点出发,按照密度可达的条件不断往外扩张得到一个最大化的区域.如果初始点是核心点,那么这个最大化的区域就是一个类,而如果初始点为边界点,则会跳至下一个初始点,如果初始点为噪声点,则直接将该点标记为噪声点.
这里需要用到的定义与记号如下:
1.ε邻域:设x∈X,称Nε(x)={y∈X:d(x,y)≤ε}为x的ε邻域.显然,x本身是属于x的ε邻域的.
2.密度:设x∈X,称为x的密度.其中,ni=1(xi∈Nε(x))或0(xi/∈Nε(x)).显然,这里的密度代表x的ε邻域内所含数据点的个数.
3.核心点:设x∈X,并且ρε(x)≥M,则称x为一个核心点.记全体核心点组成的集合为Xc,同时记所有非核心点组成的集合为Xnc=XXc.
4.边界点:设x∈Xnc,且∃y∈Nε(x)∩Xc,即x本身非核心点,但其ε邻域内存在核心点,则称x为边界点.记Xbd为全体边界点全体组成的集合.
5.直接密度可达:设x,y∈X,满足:(1)y∈Nε(x);(2)ρε(x)≥M,即x为核心点,则称y是从x直接密度可达的.显然,若x,y都是核心点,那么直接密度可达这个概念对于这两个点来说具有对称性,然而,对于其中一个点是边界点的情况来说,直接密度可达的概念对于这两个点来说并不是对称的.
6.密度可达:设x,y∈X,如果存在一系列的点x1,x2,...,xn,其中x=x1,y=xn,使得xi+1是从xi直接密度可达的,则称y是从x密度可达的.密度可达是直接密度可达的推广,这种关系具有传递性,但不一定具有对称性.
7.密度相连:设x,y,p∈X,若x,y都是从p点密度可达的,则称x,y是密度相连的.显然密度相连具有对称性.
8.类:设集合C为数据集X的一个非空子集,满足:(1)对于∀x∈C:若y是从x密度可达的,则y∈X;(2)对于∀x,y∈C,x,y是密度相连的.则称集合C为X的一个类.
9.噪声点:设C1,C2,...,Ck为数据集中的所有类,x∈X且满足x/∈Ci(i=1,2,...,k),则称x为噪声点.由于DBSCAN算法最终会将边界点也分配至某个类中,因此噪声点也可以定义为:若x∈X,且x∈X(Xc∪Xbd)则称x为噪声点.
DBSCAN算法伪代码见算法1,其作为经典的基于密度的聚类算法有诸多优点,如不需要事先指定聚类结果的数目;可以发现任意形状的聚类,甚至可以发现环状结构的类;能发现集中的噪声点,而且对于离群点不敏感等.但也存在着一些缺点:如当不同类的密度差距很大时,参数ε的选择将会十分困难,一个全局固定的ε值可能不适合所有的类.此外,ε的微小改变可能导致聚类结果的完全不同;聚类结果依赖于距离的定义,即不同的距离公式选择将带来不同的聚类结果.需要用一个更符合实际意义的距离来描述数据点之间的相似度.

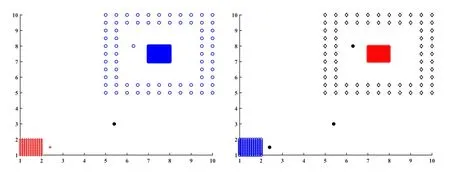
1:D B S C A N算法:ε,M: 每一个数据点对应的类标签1:令C=0 //C代表类标签2:f o r数据集中每一个未被处理过的点x d o 3: 计算x的ε邻域,并得到ε邻域内所有的点4: i f ρ ε(x) 针对上述DBSCAN算法的缺点,本文提出两个方面的改进. DBSCAN算法具有参数选择困难以及对参数敏感的缺陷,已经有许多学者提出了各种选择参数的方法或者是改进算法的方案.Feng P等人[13]运用Halkidi M等人[14]提出的方法,采用试聚类的方法选出最优参数,但是聚类耗时久.夏鲁宁等人[15]通过分析数据集的统计特征,运用逆高斯分布拟合的方式自适应地确定ε的取值,再通过噪声点的分布选择M的取值.使用该算法无需人工输入参数,但是对于存在多密度的数据集聚类效果不理想.李宗林等人[16]通过核估计的方法自适应确定了参数,但是仍然不能解决多密度数据集中聚类效果不理想的问题.也有只针对参数ε,不考虑参数M的改进.Halkidi M等人(参见[14])提出通过以下方法画出自变量为ε的轮廓系数曲线来确定最优参数.即,对于给定范围内不同ε: 1.采用DBSCAN传统算法试聚类; 2.计算数据集中每一个点x∈Ci⊆X的轮廓系数(参见[17]): 其中,a(x)表示x与x所属类内其他元素的平均距离,用来反映类内的紧密程度: b(x)表示x与不包含x的所有其他类的最小平均距离: |C|代表类C中含的数据点个数; 3.各个数据点轮廓系数的平均值即为整个数据集在这个给定ε下的轮廓系数.轮廓系数的取值范围为[−1,1],数值越接近1时代表聚类效果越好. 此外,也可以利用Dunn提出的DI指标[18],Davies等提出的DB指标[19]类似确定最优参数ε.但是对于多密度数据聚类效果还是不好. Ankerst M[5]提出的OPTICS算法,定义了基于核心距离的可达距离,也是依次随机选取数据集中的点作为核心点,取出该核心点的直接密度可达点并按可达距离升序排列.这样,最终得到了有序列表决策图(又称“山谷图”,横坐标是处理顺序,纵坐标是该点的可达距离).从山谷图中观察类的分布情况,从而确定阀值参数来完成聚类.如图1,阀值取1时,得到两类的同时会出现两个噪声点,阀值取3时,则只能得到一类. 图1 OPTICS聚类(左:数据集;右:山谷图) 本文从OPTICS算法中引入的核心距离排序获得启发,并将类的扩张半径选择为核心距离从而达到自适应的目的.这里设x∈X,对于给定定义的距离d(x,y),定义 为x的核心距离.简单来说,就是能使该点成为核心点的最小半径.一个点的核心距离在一定程度上可以反映该点附近的局部密度,核心距离与该点对应的局部密度成反比. 改进的主要思想是通过确定局部密度最大的点,并且按照该点的核心距离向外扩张至最大区域得到一个类.聚完一类之后将已经聚类的点去除,重复上述步骤直至局部密度最大点的核心距离大于作为终止条件的截断半径εc或者剩余点已不足以构成一类时终止.此时还未分类的点即标记为噪声点.改进算法的伪代码详见算法2. 2:改进算法:ε c,M: 每一个数据点对应的类标签1:令C=0 //C代表类标签2:w h i l e数据集中剩余点的个数≥M d o 3: 计算剩余每个点的核心距离d core(x),并且将核心距离最小的点x作为初始点4: i f d core(x)>ε c t h e n 5: 终止算法,并输出类标签6: e l s e 7: C=C+1 //以x为核心点,建立新类8: 取ε=d core(x)9: 计算x的ε邻域,得到ε邻域内所有的点1 0: f o r x邻域中的每一个未被处理的点p d o 1 1: 计算p的ε邻域1 2: i f ρ ε(p)≥ M t h e n 1 3: 将p的ε邻域内所有的点扩充至x的邻域内1 4: e n d i f 1 5: i f p不属于任何类t h e n 1 6: 将p添加至第C类中1 7: e n d i f 1 8: e n d f o r 1 9: 去除数据集中已被标记为C的点2 0: e n d i f 2 1:e n d w h i l e 与DBSCAN传统算法对比,改进算法主要有四点新特性: 1.每一次扩张类时选取的局部高密度点的核心距离,即扩张半径是动态变化的.可以自动地识别数据集内的多重密度选择合适的半径进行类扩张.得到的不同类间存在密度差异,每一个类内的密度固定且均匀.解决了传统算法对多密度数据聚类效果较差的问题; 2.作为一个终止条件的新参数截断半径εc对于聚类结果相对比较稳定.增大截断半径会导致继续在未分类的数据点中尝试提取新的类,但是对于之前已经聚完类的数据点来说没有影响,这大大降低了聚类结果对于参数的敏感性; 3.需要对核心距离的排序来选择局部密度最大的点作为初始点,而非随机选择.当数据量非常巨大时,排序带来的时间复杂性会比较明显.但形成的类按类内密度从小到大排序,赋予了类标签额外的含义.除了噪声点的类标签数值为0之外,类标签的数值越小,那么对应的类内密度也就越大.而传统算法的类标签仅仅代表某个数据点属于某一个类而没有其他的信息.此外,通过输出每次扩张半径,可以观察不同类之间的密度变化以及半径膨胀的速率; 4.每次聚类的初始点都是局部密度最大的点,噪声点一定存在于尚未分类的点中.因此不需要对噪声点进行判断,同时当截断半径选择较小时,也不需要遍历所有的数据点.这对算法性能有一定程度的提升. 改进算法对数据集内的多重密度可以自适应自动地识别为不同的类,能够最大限度地发现潜在的类,聚类“分辨率”高.但是,当需要低“分辨率”聚类时,效果就可能不能尽如人意. 这方面的改进主要针对需要解决的具体问题.把两个基金在各个股票上的持股比例向量看作为高维Rn空间中的点x=(x1,x2,···,xn)T和y=(y1,y2,···,yn)T,常用的 传统距离有: 1.闵可夫斯基距离: 这里p≥1,常用的取值为1,2,+∞. 2.余弦距离: 当x和y非负时,余弦距离的取值范围为[0,1]. 假设A,B,C三个基金,它们各自持有S1,S2,S3三支股票的比例向量分别为:A:(1,0,0)T,B:(0,1,1)T和C:(5,0,0)T.经过简单的计算得到两两间的欧氏距离(p=2的闵可夫斯基距离):dAB=1.7321,dAC=4.0000,dBC=5.1962.可见,基金A与基金B的欧氏距离更小,原则上代表这两个基金的持股信息更接近,也就是说基金A与基金B应该被分入同一类.然而从投资组合的角度出发,基金A与基金C都只在第一支股票上有投资,而基金B投资在第二和第三支股票上,而在第一支股票上没有投资,可以说从投资组合上看,基金A与基金C相对于基金A与基金B来说更接近.因此,闵可夫斯基距离不能刻画投资组合上的相似度. 另一方面,余弦距离更侧重刻画整体相似性,但整体相似性会由于个别分量占比相对较大而显得不同.假设A,B两个基金在5支股票上的持股比例向量为A:(1,2,3,7,0)T,B:(1,2,3,0,7)T.基金A与基金B在前三支股票中的持股比例高度相似,但这两个基金的持股大头在不同第四和第五支股票上,余弦距离也不能很好地刻画这种情况下的相似度. 针对这种情况,解决方法是引入一个新的参数作为权重调节,统筹考虑整体的相似度以及两个基金持股重合部分的相似度,这样能够得到更符合用户要求的自定义距离: 1.计算两基金对于所有股票持股比例向量x=(x1,x2,···,xn)T和y=(y1,y2,···,yn)T的余弦距离:dcos(x,y); 3.根据事先设定的,代表用户关注偏向的参数α∈[0,1],计算基于每支股票的自定义距离: 可见,α越靠近1则越关注整体相似性,越靠近0则越关注两个基金持股重合的部分. 此外,实际中的数据除了具体每支股票S持股百分比的信息之外,还能查到每支股票所在的行业板块标识,例如:金融,工业,房地产等.通过合并属于相同行业板块B的各支股票的持股百分比,可得各行业板块的持股比例向量p=(p1,p2,···,pN)T和q=(q1,q2,···,qN)T(N≤n)和重合持有板块的持股比例向量和. 同样得到基于行业板块的自定义距离: 集合针对各支股票和各个板块的信息,得到A,B两个基金间的自定义综合距离: 参数β∈[0,1]代表用户对于行业板块信息的关注程度,取值越大代表越重视行业板块的信息. 通过数值实验,可以验证改进算法的有效性. 为了反映针对ε的改进算法2在多密度数据集合中的聚类效果,构造了如图2所示的二维数据点集合. 图2 人工模拟数据集 该数据集含有三个类,包括一个高密度类C1(“+”),一个中密度类C2(“◦”)以及一个低密度的环状结构类C3(“ƒ”),此外包含了a,b和c三个噪声点(“•”).对于DBSCAN传统算法与改进算法,统一取M=4,分别取ε=εc=0.5,0.8进行聚类.聚类结果见图3和图4. 实验结果图中,“+”代表第一类中的数据点,“◦”代表第二类中的数据点,“ƒ”代表第三类中的数据点,“•”代表噪声点.如图3所示,ε=0.5时传统算法成功识别了三类,没能识别出离群噪声点c,并将其归为C2类.如图4所示,ε=0.8时传统算法将C1和C3以及噪声点a都归入了同一类,同时噪声点c也被归入了C2类.但两种情况改进算法都正确进行了聚类,同时发现不同εc并没有导致聚类结果的改变,可见改进算法对于输入参数的依赖性不大.此外,改进算法得到的类标签(符号)正好对应从大到小排列的类密度.这有助于更全面地了解数据集的分布性质. 图3 ε=εc=0.5时的聚类结果(左:传统算法;右:改进算法) 图4 ε=εc=0.8时的聚类结果(左:传统算法;右:改进算法) 这里选用了深圳交易所2017年第三季度的数据(已经过脱敏处理)来验证改进算法的有效性.由于数据点是高维数据点,聚类效果很难可视化展现,只能随机筛选部分结果,以表格的形式来加以说明. 4.2.1 传统算法下,综合距离对比传统距离 实验中使用的参数取值为α=0.5,β=0.2,M=3.基于试聚类得到的轮廓系数曲线(如图5所示),选择ε=0.14作为参数.综合距离和欧氏距离的部分聚类结果如表1所示.数字代表聚类后基金所属的类标签.可见综合距离将“中欧”系,“交银”系,“兴全”系和“民生”系全部准确聚类.特别是观察“民生”系三个基金(基金代码136,690003和690009)的持股情况(如表2所示),可以看到这三个基金的投资组合非常相似,事实上它们也确实隶属于同一家基金管理公司,属于同一个信息群落. 图5 轮廓系数随参数ε变化曲线 表1 综合距离和欧式距离的部分聚类结果 表2 “民生”系三个基金的持股情况 其次,再对比综合距离和余弦距离的聚类结果,结果如表3所示.同样可以看到,余弦距离与综合距离的差距主要集中在“国联”系(基金代码4326和4327)两个基金的聚类上.这两个基金前十支股票的持股情况中(见表4),有八支股票是共同持有的,并且在共同持有的股票中,持股的比例也相当接近.而在剩余的持股不同的四支股票中,建设银行和农业银行持股份额比较大,宁波银行和北京城建的持股比例相对较小.正是这两只持股份额较大且完全不同的股票对聚类结果产生了主要影响,造成余弦距离下的错误聚类.此外,这两只股票同属于“银行”板块,因此考虑了板块影响的综合距离就更容易得到正确的聚类结果了. 表3 综合距离和余弦距离的部分聚类结果 表4 “国联”系两个基金的持股情况 4.2.2 基于综合距离,改进算法对比传统算法 取前面同样的参数.聚类结果如表5所示,可以发现“汇添富”系的两个基金(基金代码519066和519068)在改进算法中被单独聚为一类.取出这两个基金的持股信息并与“汇添富”系的其它两个基金(基金代码2419和2959)对比(见表6).它们持股比例前十支的股票中有六支是共同持有的,这四个基金同属一家基金管理公司,被传统算法分为一类是合乎逻辑的.但是仔细观察可以发现,这四个基金之间确实存在不同的子类,如前两个基金对美的集团的持股比例都在4%至5%之间,而后两个基金的持股比例都在9%至10%之间;前两个基金均没有在华帝股份与南极电商上持股,但是都在中远海控上持股且持股比例十分接近.而后两只基金均在中远海控上空仓,但在华帝股份与南极电商上有较高比例的持股.因此,这四个基金确实应该被分为两类,这验证了改进算法能够比传统算法提取出更紧密的类. 表5 传统算法和改进算法部分聚类结果 表6 “汇添富”系的四个基金持股情况 4.2.3 发现疑似关联基金 同属一家公司下的基金存在关联关系显然是合理的.作者更希望发现不属同一公司,但涉嫌存在背后信息交流的关联基金.表7给出了基于前述数据聚类后疑似关联性最强的一组结果.前两只基金分别为长安产业精选灵活配置混合型发起式证券投资基金(基金代码496)和长安产业精选灵活配置混合型发起式证券投资基金(基金代码2071),同属一个基金管理公司.第三只基金为金元顺安新经济主题混合型证券投资基金(基金代码620008),基金管理公司显然不同.这个结果和2018年《国际金融报》的报道相符合(参见[1]). 表7 疑似关联基金 致谢本文的研究基于深圳证券交易所在上海财经大学举办的“中-加量化金融问题联合研讨会暨全国2018金融数学与金融工程Team Workshop”上提出的相关课题(参见[20]).感谢深圳证券交易所提供的数据.§3 改进的DBSCAN算法
3.1 针对参数ε的改进

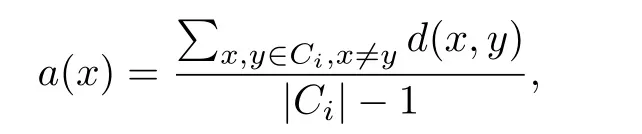
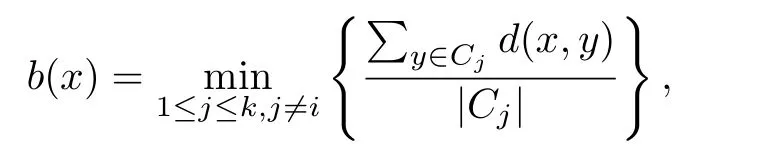

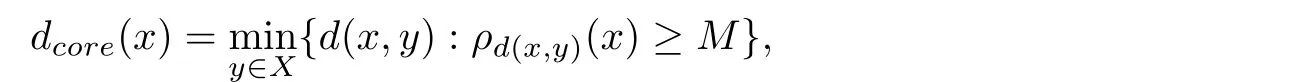

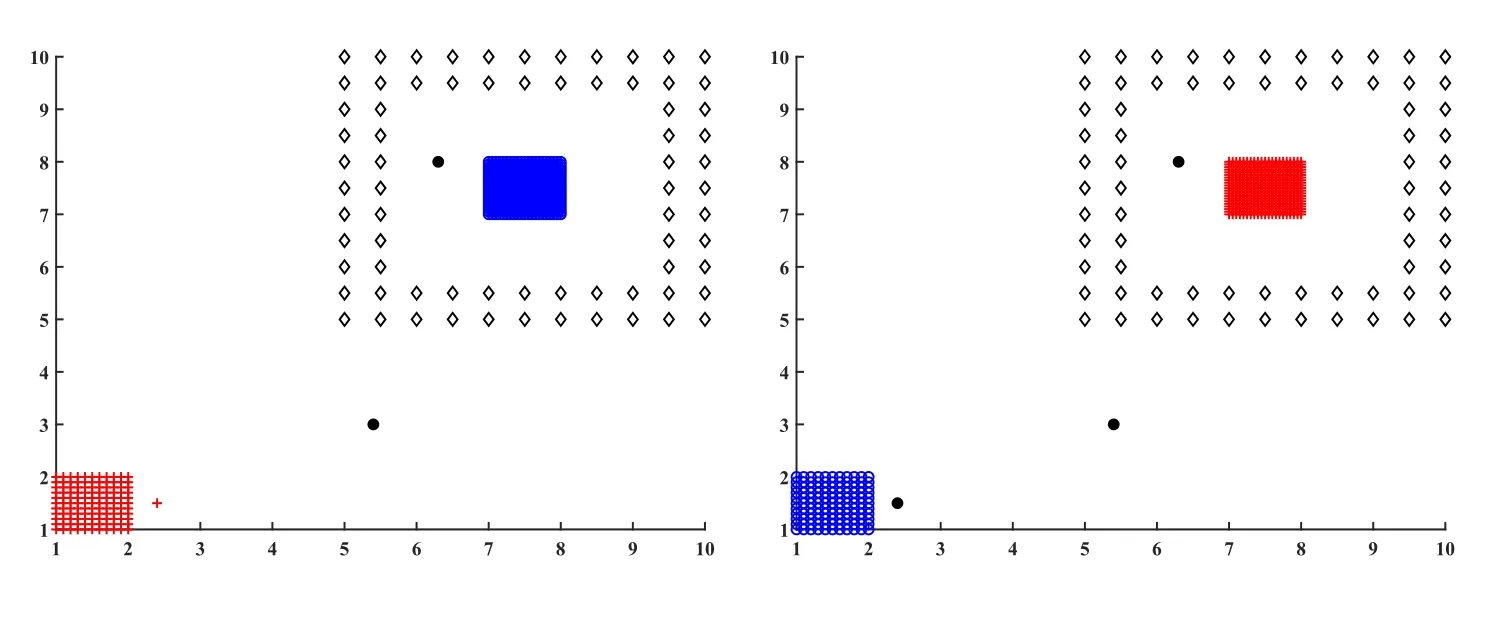
3.2 距离的选择

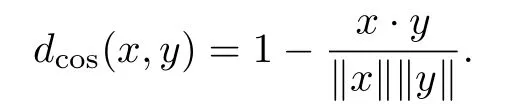
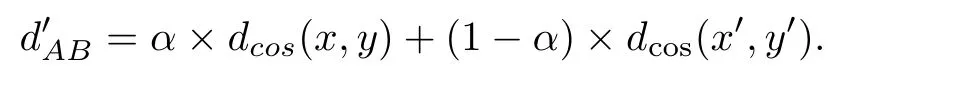
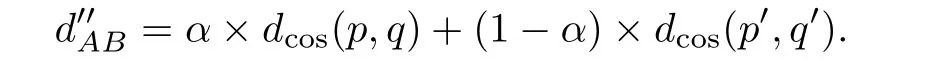

§4 数值实验
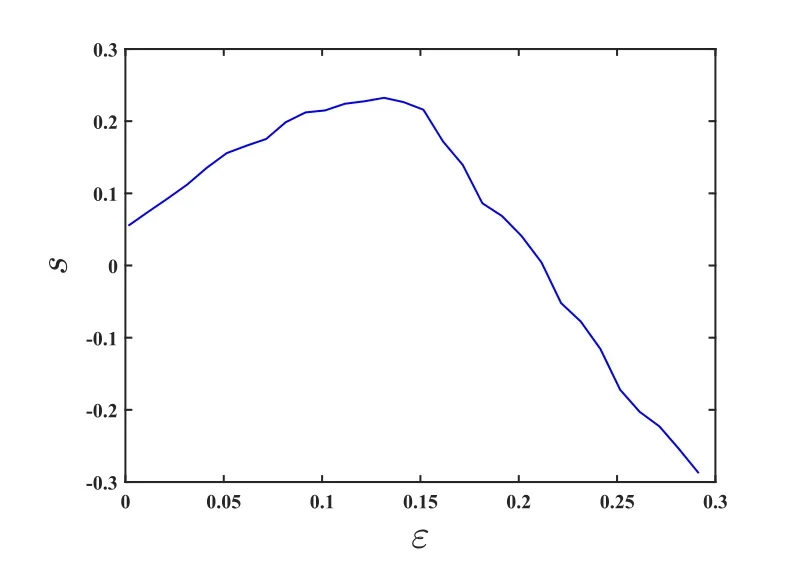
4.1 针对ε的改进算法的有效性

4.2 发现公募基金信息群落上的应用