稳定Hawkes过程下的保险公司分红问题

陈亦令,边保军

(同济大学数学科学学院,上海200092)

§1 引 言

保险公司分红问题在集体风险理论中是一个经典问题.从公司金融的角度来看,公司价值可定义为破产前股东所得红利的期望现值.如何最大化公司价值一直是业界关心的问题,同时股东希望从投资中获得分红利润.因此采取何种分红策略使得贴现的分红最大一直是精算界的热点.当索赔事件由常系数跳跃强度的泊松过程描述时,称之为经典Cram´er-Lundberg模型.经过学者多年的探究,这种假设经不住事实的验证.实证研究表明索赔事件有时会在短时间内成群出现.也就是说,一项重大索赔事件之后伴随着一系列索赔事件.例如,在2008金融危机期间,信用保险公司短期内受理的索赔事件快速增加.又例如,自然灾害的发生冲击大量受保人的利益,影响公司价值.但是,很少有研究者提出带有族群特性索赔事件的风险过程.Hawkes1971年首次提出Hawkes过程[1]来描述短时间内发生多次跳跃的现象.Bacry等[2]的研究验证了Hawkes过程在金融市场的应用价值.

随着现代随机控制理论的发展,经典的保险公司最优分红问题引起了越来越多学者们的关注.许多问题应运而生,例如:保险公司盈余过程模拟,最优分红策略,生存概率问题以及现实金融活动下的条件拓展.在此,Albrecher[3]和Avanzi[4]总结前人研究,给出了两篇综述文章.Azcue和Muler[5]在经典Cram´er-Lundberg模型下,探究了带投资的最优分红问题,并且证明了带状策略的最优性.Chen和Bian[6]在变化分红上界条件下,探究了保险公司最优分红和最优投资策略问题.孙宗岐与陈志平[7]考虑索赔次数服从复合Poisson-Geometric过程,探究了保险公司的最优投资-再保-混合分红策略问题.

Hawkes过程用于描述索赔事件的自激励特性与族群特性,应用到保险公司价值研究起步较晚.Gao和Zhu[8]探究了线性Hawkes模型下的中心极限定理,并运用到保险公司生存概率问题.Stabile和Torrisi[9]利用Hawkes过程描述带有族群特性的索赔事件,并探究了保险公司生存概率问题在轻尾条件下的无限和有限破产概率的渐进行为.Hainaut[10]分析了金融市场和保险市场之间存在传染特性下的保险公司资产管理政策.李亚男等[11]考虑到,保险公司承担的风险是相关的,探究了保险公司最优分红和再保险问题.然而,大量文献中的索赔过程一直都是由常系数泊松过程描述,且涉及Hawkes过程来刻画索赔过程的分红问题更是少数.因此,引入Hawkes过程来描述索赔事件的族群特性,探究保险公司的最优分红问题:寻找分红策略,使得保险公司在破产时分红最大化.

本文中索赔事件由Hawkes过程描述,它的索赔跳跃强度具有自激励和回归特性,造成跳跃族群现象.运用随机控制理论,探究了稳定Hawkes模型下的保险公司最优分红问题,并将优化问题转化为求解一个非线性Hamilton-Jacobi-Bellman(HJB)方程.该方程是一个非线性微分积分方程,研究解的存在唯一性具有重要意义.探究了目标函数的有界性和连续性,并在粘性解的框架下给出了解的存在性.同时,给出验证定理:目标函数还可以被验证为相应HJB方程的最小粘性上解.启发式的介绍了障碍线策略,并在数值模拟部分给出了一个具体分红过程.

本文的主要结构如下.§2讲述了Hawkes过程以及具体的保险公司分红模型构建.§3给出了目标函数的有界性和连续性,并介绍了粘性解的定义.§4在粘性解的框架下证明了目标函数是相应HJB方程的粘性解,并给出了验证定理.§5进行了数值模拟与结果展示.

§2 模型构建

Hawkes过程是一类具有随机波动率的泊松过程.换句话说,该过程是一个具有自激励性质的计数过程.用Nt=N(0,t]指代(0,t]时刻内索赔事件发生的次数.给定概率空间(Ω,(Ft)t≥0,P),计数过程{Nt}t≥0满足:

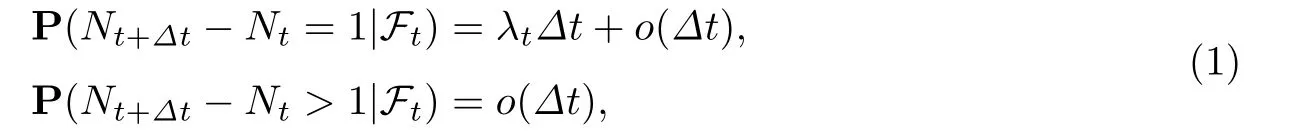
其中,λt为索赔跳跃强度,满足如下随机微分方程:

正如图1中所示,在短时间内,一个索赔事件很可能伴随着一系列的索赔事件.同时假设0≤β<α,均值回归性质保证了索赔跳跃强度不会趋于无穷,确保索赔跳跃强度过程稳定性.

保险产品定期接受保费,承担不定期到来的索赔事件,同时按策略分红给持有者.保险公司的产品投资组合的盈余过程如下:

图1 Hawkes过程与保险公司盈余过程模拟路径

其中,x为初始资金;p为单位时间内收到的保费;Yi为索赔额,独立同分布于分布函数F.假设p>E[λtYi],使得保险公司的盈余过程期望意义上不会破产.图1也给出了一条无分红过程的盈余过程Xt的模拟路径.

累积到t时刻的分红总量为:

其中,为连续分红过程.若分红率为qs,则.离散部分表示保险公司可以立即拿出部分盈余作为红利.索赔过程由Hawkes过程描述.假设立即分红量不能超过现有的公司盈余.换句话说,分红不能导致公司破产.

满足以上条件的分红策略记为可行分红策略l,假设Lx,λ是所有可行分红策略的集合.执行一条可行分红策略l,对应的破产时间为:

可以看出,公司破产只可能发生在索赔事件到来之时.目标函数为:

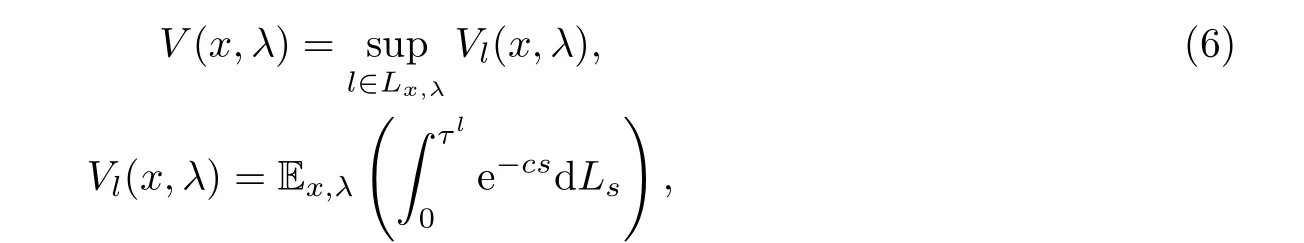
其中c是一个常系数贴现因子.整个优化问题可以归结为寻找最优的分红策略,使得保险公司到破产时刻分红贴现的期望最大化.为了简化问题,只考虑股东当前的最大利益,这也是保险公司中的一个经典问题,以此来评价一个保险组合.

为了表述方便,假定R+=[0,+∞),并且V(x,λ)=0当x<0.假设目标函数足够光滑,通过动态规划原理,得到此优化问题对应的HJB方程:

其中

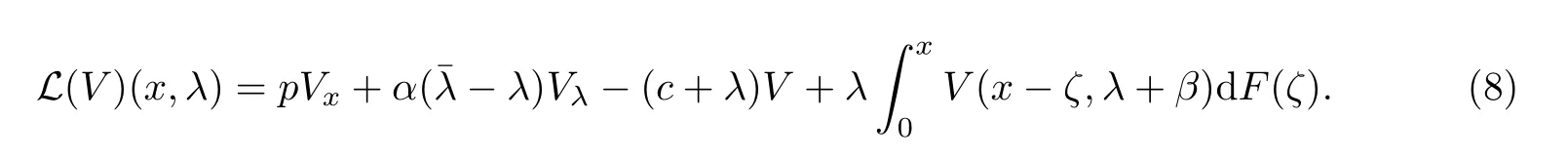
§3 预备知识

命题 3.1目标函数(6)满足

证第一个不等式显然成立,因为保险公司可以立即将公司盈余全部分红.对于任意l∈Lx,λ,有,所以

结论得证.

命题 3.2目标函数(6)关于x和λ连续.

接下来给出本文优化问题的动态规划原理(Dynamic Programming Principle).详细证明过程类似于[12],在此不再赘述.

命题 3.3对于任意x≥0,λ≥0和任意停时τ>0,有

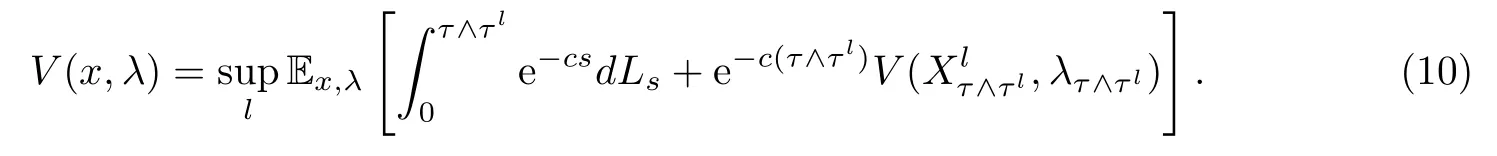
由于HJB方程(7)是一个高度非线性的微分积分方程,目标函数的光滑性很难在经典解的意义下满足HJB方程(7).因此,介绍一种由[13]提出的一种弱解:粘性解(Viscosity Solution).

定义3.1连续函数:R+×R+→R是HJB方程(7)的粘性上解,当且仅当对于任意连续可微函数ϕ都有

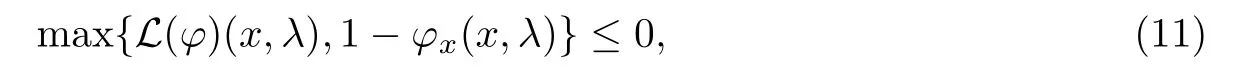
连续函数:R+×R+→R是HJB方程(7)的粘性下解,当且仅当对于任意连续可微函数ψ都有

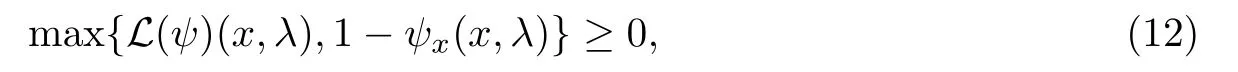
最后连续函数u是HJB方程(7)的粘性解,当且仅当u是HJB方程(7)的粘性上解和粘性下解.

§4 主要结果

4.1 解的存在性

命题 4.1目标函数(6)是HJB方程(7)的粘性上解.

命题 4.2目标函数(6)是HJB方程(7)的粘性下解.

证假设目标函数(6)在(x0,λ0)点处不是粘性下解.考虑任意可行策略l∈Lx0,λ0,断言,对于任意†>0,存在h>0和一个连续可微函数ψ,使得

假设目标函数(6)在点(x0,λ0)处不是粘性下解,则存在η和连续可微函数,使得在(x0,λ0)达到局部最大值,并且有

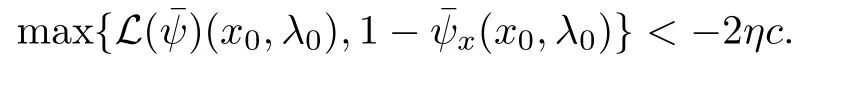
由命题4.1和命题4.2,得到以下定理:

定理 4.1目标函数(6)是HJB方程(7)的粘性解.

4.2 验证定理

由于该问题在零点处边界条件的天然缺失,比较原理的证明存在困难.采用Azcue和Muler[5]中的办法,给出了类似的验证定理,探究解的唯一性.在给出验证定理之前,阐述以下条件

(A.1):u关于x,λ局部利普希茨(Lipschitz);

(A.2): 存在常数M>0,使得u(x,λ)≤M(1+x+λ).

由命题3.1和命题3.2,知道目标函数(6)满足条件(A.1)和(A.2).

在此对分红策略进行初步的定性研究.索赔过程不具有族群特性的一维保险公司最优分红问题中,障碍策略被证明是最优策略.假设分红障碍为b,当盈余大于b时,支付盈余超过b的部分为红利;当盈余等于b时,定期收取的保费当作分红;当盈余小于b时,不进行分红.然而,根据随机控制理论,最优控制(分红策略)一定是公司盈余和索赔跳跃强度的函数,原来的障碍策略失效.引进索赔跳跃强度,将障碍点拓展成障碍线.根据HJB方程(7),可以将R+×R+分成三个子集.

定义 4.1定义P=A∪B∪C,其中:

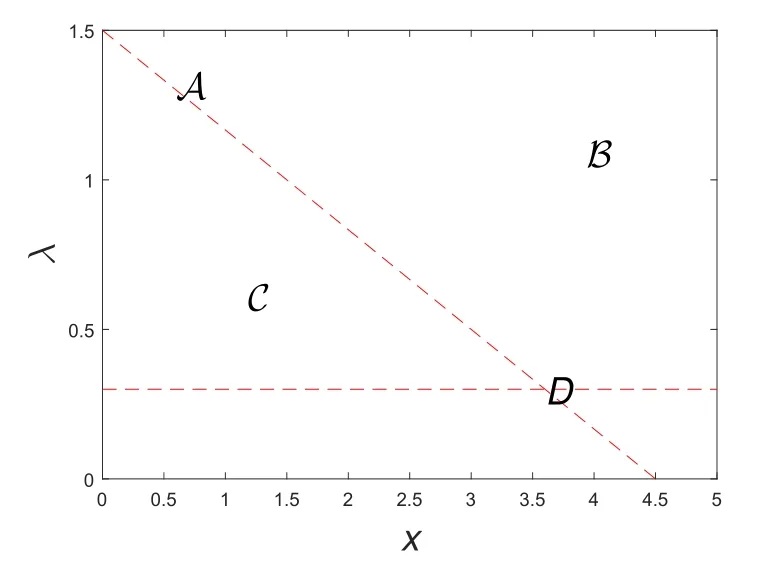
图2 分红区域划分

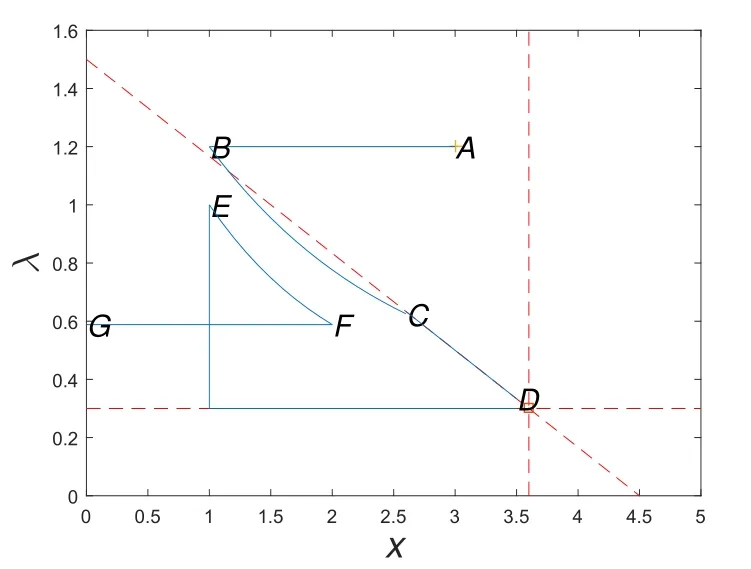
图3 一个最优分红策略的例子

区域A蕴含着一个函数ρ:R+→R+, 使得1−Vx(ρ(λ),λ)=0和L(V)(ρ(λ),λ)=0.称A={(ρ(λ),λ)∈R+×R+}是一条障碍线.

图2简单展示了定义4.1中的分红区域划分.定义4.1蕴含着一个分红策略,简述如下.为了直观展示,将障碍线ρ(λ)简化成一次函数.水平虚线是指平均索赔跳跃强度.简单的说,假如当前资产和索赔跳跃强度位于A,适当分红,使得资产和索赔跳跃强度仍然在障碍线上,直到索赔到来.假如当前资产和索赔跳跃强度位于B上,资产盈余较多,立即拿出部分资产分红,使得资产水平平移到障碍线A上.假如当前资产和索赔跳跃强度位于C,资产盈余较少,不分红,直到离开区域C.

图3给出了定义4.1分红策略下的一个资产组合盈余状态的变化路径.初始盈余和跳跃强度为A=(xA,λA)∈B,且λA>,模拟路径为A→B→C→D→E→F→G.其中:A→B:立即支付xA−xB;B→C:不分红;λt回归到水平线,Xt线性增长;C→D:支付ptCD−ρ(λD)+ρ(λC) 作为红利,其中,即不发生跳跃时,从C到D的时间,使得Xt仍在障碍线上;当处在D点,以保费率p连续分红,此时Xt和λt不变,直到索赔到来;D→E:索赔到来,盈余过程上跳,跳跃强度下跳;E→F:与B→C段类似,不分红;F→G:一个大索赔事件到来,保险公司破产.

§5 数值结果

对HJB方程(7)进行差分数值求解,并给出了目标函数和最优分红策略的数值结果.HJB方程的差分格式建立参考Forsyth[14]中的方法.在零点处边界条件的缺失阻碍了差分格式的建立.因此,人工补齐缺失的边界条件.首先,数值求解L(V)=0,然后对得到的解进行改进,使得其满足1−Vx=0,具体的改进方法可见Azcue和Muler[3].

相应的定解条件和人工边界条件为

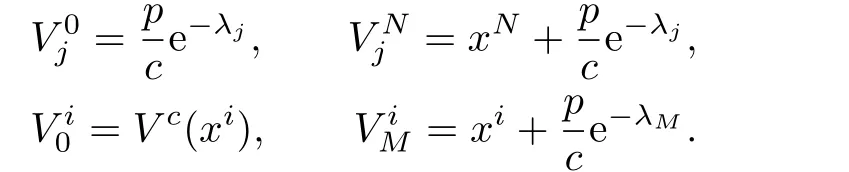
其中,Vc是常系数λ=0.1的最优分红问题的连续解,以此来给出V在λ=0处的初始值.

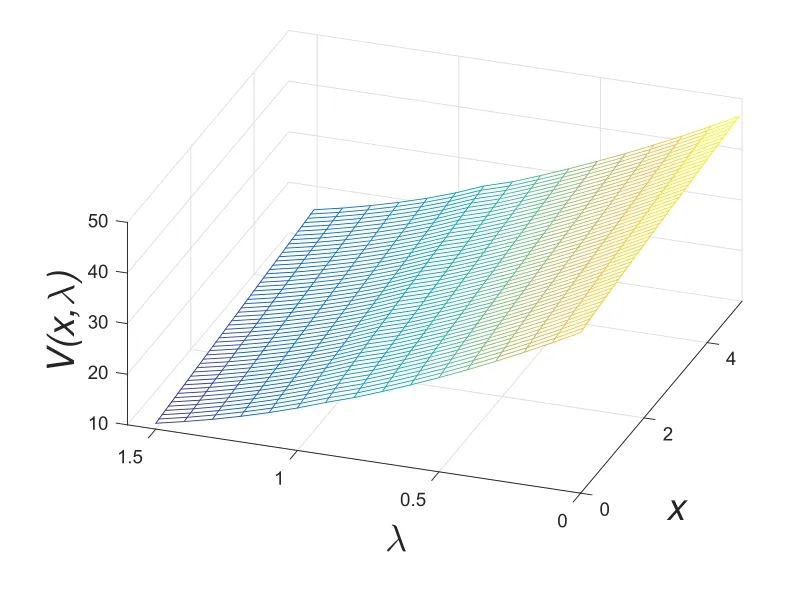
图4 目标函数的数值结果三维图

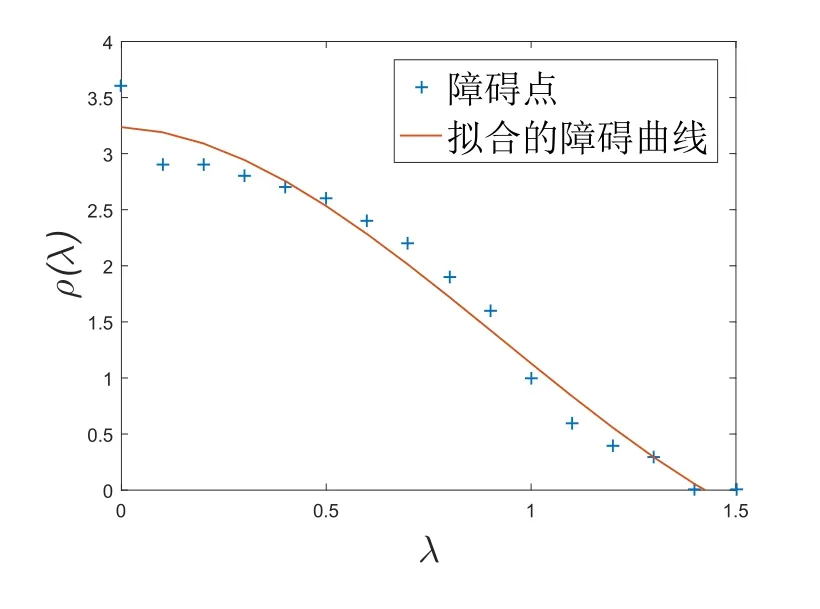
图5 最优分红策略中的障碍线

图4展示了目标函数数值解的三维图.图5展示了障碍线的点点图和多项式拟合.首先,策略控制必定是资产盈余和索赔跳跃强度的函数,不是时间的函数.可以看到,ρ(λ)关于λ非增.当λ小时,索赔事件偶尔发生,盈余保持较高水平,下降的慢;当λ大时,ρ(λ)下降的快,分红障碍低,保险公司需要立即拿出部分盈余分红,防止索赔事件连续到来使得公司破产而无法分红.正是由于自激励性质的存在,当λ足够大时,索赔事件在短时间内接连发生,出现族群现象.

§6 结语

实证研究表明,索赔事件具有族群特性.引入Hawkes过程刻画短时间内发生多次索赔事件的现象,探究了保险公司的最优分红问题.利用动态规划原理,将优化问题转化为求解一个非线性HJB方程,在粘性解的框架下给出了解的存在性.同时,目标函数还可以被验证为HJB方程最小的粘性上解.最后,进行了数值计算,并定性的分析了具体的分红策略.最优分红策略与当下保险公司盈余和索赔跳跃强度有关.简单来说,根据当下盈余和跳跃强度与障碍线的关系做出分红操作.数值结果发现,当索赔跳跃强度非常大时,索赔事件在短时间内连续发生,保险公司需要立即拿出部分盈余分红,防止索赔事件连续到来,使得公司短时间内破产而无法分红.

致谢作者衷心感谢审稿人提出的宝贵建议.