一类非线性年龄等级结构种群系统模型的可控性
2020-07-07何泽荣韩梦杰
何泽荣,周 楠,韩梦杰
(杭州电子科技大学运筹与控制研究所,浙江杭州310018)
§1 引 言
种群动力系统的可控性问题既重要也较为困难.基于个体特征差异(如年龄、尺度)的连续种群模型,通常形为偏微分-积分方程,且具有全局反馈形式的边界条件,属于一类新的无穷维状态系统,其可控性研究颇为不易,参见[1-13]及所引文献.在绝大多数生物种群中,生态学家们都发现了个体之间的等级或地位差异,参见综述论文[14]及所关联的200多项生态学研究成果.为了定量理解这类种群的演化行为,学者们建立了一些等级结构种群动力学模型(见[15-25]),并进行了较为深入的研究,其结果可以很好地解释某些用其它种类模型难以解释的生态现象.
另一方面,关于这类系统模型的可控性问题,似乎未见公开的成果报道.本文力图解决一类年龄等级结构种群系统的近似可控性问题,它具有较强的非线性,采用个体迁移作为分布式控制手段.运用冻结系数法、线性系统可控性和集值映射不动点原理确立非线性系统的可控性.
§2 系统模型
本文研究下述由个体年龄决定的等级结构种群系统动力学模型的近似可控性.
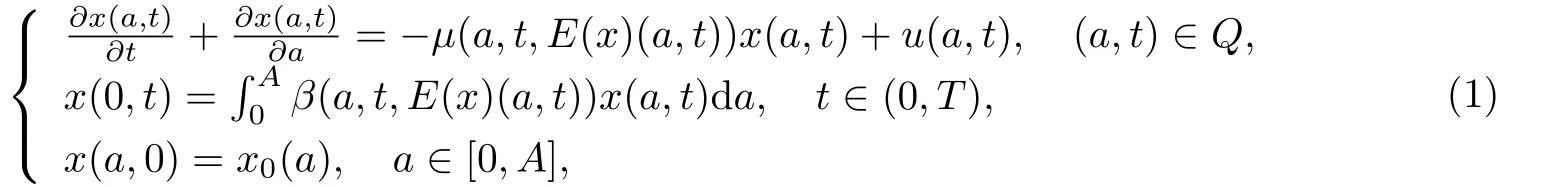
其中描述种群中个体竞争的“内部环境”E(x)定义为

α代表相对年长的个体加权系数.与年轻个体相比,年长个体的竞争力较弱.在系统(1)-(2)中,Q=(0,A)×(0,T),常数A为个体的最大年龄,T为调控周期.x(a,t)代表t时刻的种群年龄分布密度,函数参数µ和β分别表示个体的平均死亡率和繁殖率,它们都与内部环境E(x)有关.函数x0(a)给出种群的初始年龄分布,u(a,t)表示人对个体的迁移率(投放或者移出),它满足约束
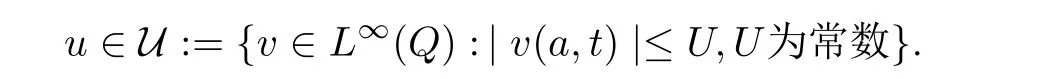
出于生态意义和理论分析需要,假定下列条件成立.
(A1)死亡率µ(a,t,s)在Q×[0,+∞)上连续,µ(a,t,s)>0且对任意固定的t有


(A2)繁殖率β(a,t,s)在Q×[0,+∞)上连续,并且0≤β(a,t,s)≤,为正的常数.
(A3)对给定的(a,t)∈Q,µ(a,t,·)单调不减,β(a,t,·)单调不增;β与µ关于第三个变量s局部Lipschitz连续.
(A4)存在正常数,使得
注2.1文[25]已经对系统(1)-(2)的适定性作了分析,得出结论:对任意给定的u∈U,系统(1)-(2)存在唯一解.
§3 近似可控性
通过实施个体迁移,能否将种群分布从当前状态调节到预定状态?这是所谓可控性问题.先给出如下精确定义.
定义3.1对任意给定的初始分布x0∈L∞[0,A],终态分布∈L∞[0,A]和误差ε>0,如果存在u∈U,使得系统(1)-(2)相应的解xu(a,t)满足

那么称系统(1)-(2)在区间[0,T]上近似可控.
处理可控性的主要思路:首先固定种群的内部环境,此时的模型退化为线性系统,其近似可控性结果已知.然后研究某个与解有关的集值映射,严格证明其不动点的存在性.由此获得系统(1)-(2)的近似可控性.
任意固定环境函数E(x)为X.考察下列线性系统

利用假设(A1)-(A4)和文[6]中定理4.1可推知:上述系统(3)在L1(Q)中近似可控;即存在u∈U,使得系统(3)的解xu(a,t;X)满足
为了定义合乎需求的映射,需要确立系统(3)某类解集的紧性.为此先给出以下估计.



当0 再证下列紧性结果. 引理3.2下列集合 证由于在R2中是紧集.利用集合K的定义可知:任一X∈K必为上的连续函数,且K中任一序列必为等度连续.运用Arzela-Ascoli定理即得结论. 再由(21)与(23)导出:当a 最后利用(20)和(24)可得: 其中,C1与u1,u2无关. 为了建立系统(1)-(2)的近似可控性,需要下列结果.([26,p452],Theorem 9.B) 引理3.4(Kakutani) 如果下列条件成立: (1)集合H是局部凸空间Y中的非空紧凸集; (2)集值映射G:H→2H上半连续; (3)对任意y∈H,G(y)非空、闭、凸. 那么映射G在H上必存在不动点. 定理3.1系统(1)-(2)在L1[0,A]中近似可控. 证定义集值映射G:K→2K如下: 其中集合K由引理3.2给出,xu(a,t;X)是线性系统(3)的解. 由引理3.2知:K是紧集.此外,易知K为凸集.从而引理3.4的条件(1)成立. 根据文[6]的结论知:G(X)6=∅.由于函数u是线性系统(3)的非齐次项,因此G(X)必为凸集.再由引理3.3知G(X)为闭.引理3.4的条件(3)也成立. 最后验证条件(2),即证明映射G上半连续. 令序列{Xn}在L1(Q)中收敛于X,且对任意选定的un,使得E(xun)∈G(Xn)在L1(Q)中收敛于h,只需证明h∈G(X). 由关系式(5)知: 由于{un}⊂L∞(Q)⊂L2(Q),由控制集的一致有界性知:存在子序列(仍记为{un}),使得{un}在L2(Q)上弱收敛于u.此外,利用(14)可得:序列{bun}在L2(Q)中有界,因此存在子列(仍记为{bun}),使得{bun}弱*收敛于b.对(25)右端取极限n→∞,可确定下列函数: 此外,由un的选取知:令n→∞,立即导出: 综合上述过程即知:h=E(x(·,·;X)),并且h∈G(X). 总而言之,映射G满足引理3.4的所有条件,它必有不动点. 作为本文的主要结果,定理3.1意味着:存在适当的迁移策略,经过一段指定时间后,它能将种群系统的当前状态调节至人们所期望的目标状态.应当注意:这一结果的证明是纯粹存在性的而非构造性的;即证明了满足可控性要求的迁移策略一定存在,但并没有具体给出一个迁移函数的表达式.这种情况在数学对象的存在性分析中经常遇到.当模型的相关参数已知后,为了具体找出控制策略,还需进一步利用共轭梯度等数值方法计算出满足精度要求的迁移函数. 致谢作者感谢审稿专家提出的宝贵意见.

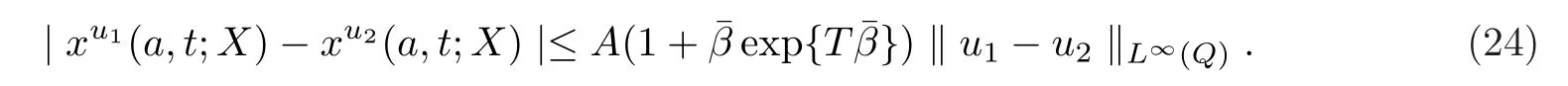
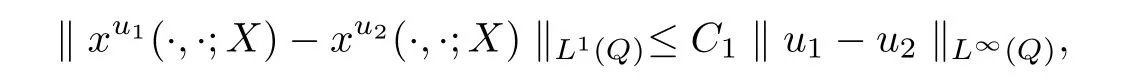



§4 结束语
