带相依辅助信息的分位数自回归模型的经验似然估计
2020-07-07杨晓蓉徐诗展赵棋炯王励励
杨晓蓉,徐诗展,赵棋炯,王励励
(浙江工商大学统计与数学学院,浙江杭州310018)
§1 引 言
常系数自回归时间序列作为一种常用的时间序列模型,在过去的几十年中被广泛地研究并应用到各个领域.近年来,随着研究的不断深入,各种随机系数时间序列模型在理论与应用中都表现出了更多的优越性,因而受到越来越多的关注.其中一个重要的研究对象就是文献[1]提出的分位数自回归模型.它在分位数的框架下,把常系数模型推广到变系数的形式.为了给出分位数自回归模型的定义,首先考察如下的p阶随机系数自回归过程:
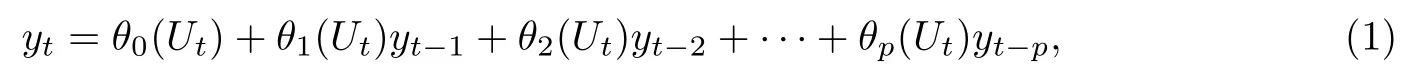
其中θj是定义在[0,1]−→R需要被估计的未知函数,{Ut}是一列服从标准均匀分布U(0,1)的独立同分布的随机变量.对任意单调递增的函数g和标准均匀分布U,令Qg(U)(τ)表示g(U)的τ分位函数,Qg(U)(τ):=g(QU(τ))=g(τ),因而当等式(1)的右侧关于Ut是单调递增时,yt的条件τ分位函数定义如下:
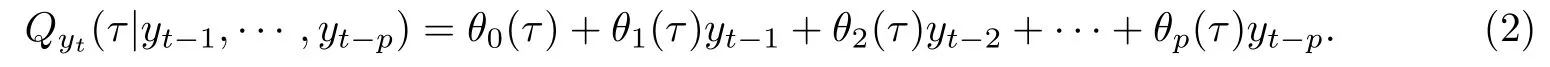
等式(2)就称为p阶分位数自回归模型(QAR(p)),可以简写成如下形式:

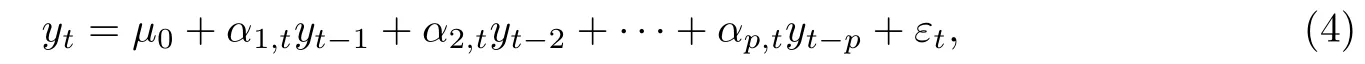
与文献[2]中的定义一致,(3)式的分位数回归估计由下式给出:
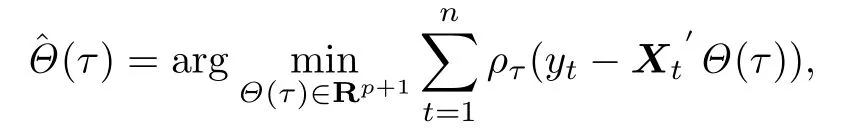
其中ρτ(x)=x(τ−I(x<0)).上述解称为自回归分位数.在一些正则性条件下,文献[1]证明了估计量的渐近正态性质,即
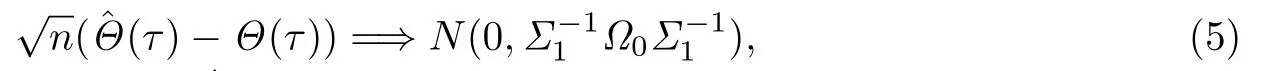
统计建模以后,一个很重要的研究内容是模型系数估计量的有效性.实际应用中,数据的采集过程会产生额外的辅助信息,这些信息本身的潜在效用能够提高估计量的效率.因此寻找合理的方法,充分利用辅助信息来提高QAR模型系数估计量的有效性,有着重要的研究意义.
下面首先给出辅助信息的表示式.令h(Zt;β)∈Rr表示含有d维(d≤r)参数β的辅助信息函数,其中Zt代表所有观测数据的集合,满足,且在给定Xt0时,h(Zt;β)是可测的. 由于模型的自回归属性,显然所定义的Zt不是独立的随机变量,并且Zt中可能包含除了模型以外的其他额外变量,而这些额外变量也允许和Xt0存在一定的关联性.不失一般性,假设h(Zt;β)满足下面的条件:

下面通过两个例子来具体说明辅助信息函数的表现形式.例如:考虑一个QAR(1)模型yt=µ0+α1,tyt−1+εt. 这里,给定一组观测,可以得到β的最小二乘估计,那么辅助信息可以表示成.又如,如果考虑β的最小绝对偏差估计,则辅助信息可以表示成h(Zt;β)=
为了更好的利用辅助信息,经验似然(EL)方法常常被用于相关的统计推断.EL方法是一种较为有效和灵活的非参数统计推断方法,最早在1988年由Owen提出并初步发展起来的(参见文献[3-5]).由于该方法具有不依赖于总体先验信息的优越性,随后的几年里有大量文献对其进行了相应的研究.文献[6]借助经验似然方法,将辅助信息用于极大似然估计.文献[7]利用经验似然的方法,得到了非参数密度估计量的区间估计.文献[8]对回归模型的经验似然方法给出了较为完整的综述.文献[9]中考虑如何利用经验似然方法提高带辅助信息的分位数回归估计.近年来,其它关于经验似然的研究可参见文献[10-14].
文献[9]研究了一般的线性回归模型,其中协变量与因变量之间是不相关的,因而辅助信息函数中的观测{Zt,t=1,···,n}被假设成独立同分布的.然而在QAR模型中,由于而{yt}是一个时间序列,此时{Zt,t=1,···,n}的独立同分布假设不再成立.因此,文献[6]中关于模型系数估计量渐近性质的推导无法直接迁移到QAR模型的研究中来.针对相依情形,§2讨论了带有相依的辅助信息的QAR模型系数的经验似然估计.且分别对于β=β0已知和β未知的两种情况,在一些正则性条件假设下,推导出了系数估计量的渐近正态性质.本文的定理2.1以及定理2.2是对文献[9]中研究结果的推广,文章通过数值模拟和实例数据应用展示了估计方法的有效性.此外,§3还讨论了随机系数线性假设Wald检验.基于§2的主要结论,容易得到所构造的检验统计量的弱收敛性质,这对统计推断起了奠定性的作用.
§2 QAR模型系数的经验似然估计
考虑到QAR模型具有自回归的结构,变量之间不再是独立的,本节首先给出相依随机变量的基本定义.
定义2.1[15]一列随机变量{ξj}j≥1被称为是α-混合的,如果当n→∞时,
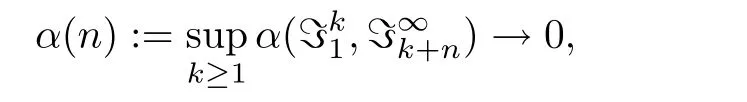
其中
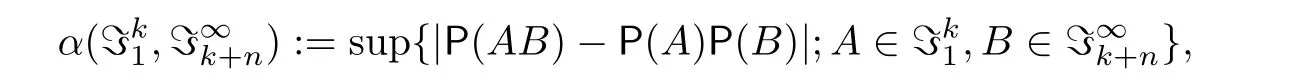
表示由ξa,ξa+1,...,ξb生成的σ-域.
混合的概念最初由文献[16]提出并研究.文献[17]就其它常用混合情形给出了一个较好的综述.α混合的概念作为弱相关的衡量尺度,在时间序列相关研究中被广泛应用.由于{yt}也是一列平稳的α-混合序列,允许(yt,Xt0)⊂Zt,因而下文中,假设观测{Zt,t=1,···,n}是一列平稳的α-混合序列.
2.1 辅助信息中参数β=β0已知
本小节首先讨论总体的先验信息已知时,QAR模型系数的经验似然估计.不失一般性,假设辅助信息函数满足E(h(Zt;β0))=0,其中β0是已知的.
令ω=(ω1,ω2,···,ωn)为一个向量,使得,且对所有的t=1,···,n,有ωt≥0.经验似然定义如下:

当β=β0时,利用Lagrange乘子法可以得到

其中λβ0满足
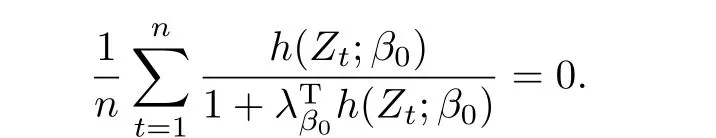
带辅助信息的分位数自回归模型系数的估计如下式:
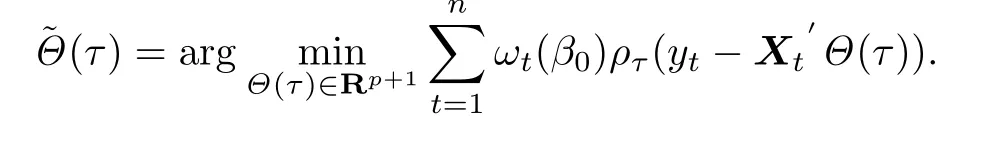
为了对经验似然估计的渐近性质进行进一步分析,引入下述正则化条件:
C1存在β0使得E(h(Zt;β0))=0. 矩阵Σ(β0)=E(h(Zt;β0)hT(Zt;β0))正定且∂h(Zt;β)/∂β在β0的一个邻域内是连续的.矩阵E{∂h(z;β)/∂β}是满秩的.此外,存在函数Gij(z)使得对落入β0邻域的β有,
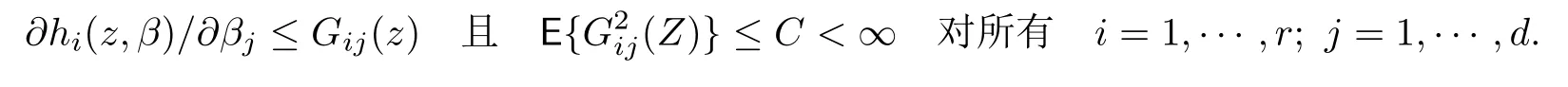
C2对所有整数k≥1,Xt与Xt+k的联合概率密度函数fX(·,·)存在且满足对所有的(u,v)∈N(x)×N(x),fX(u,v)≤C,其中N(x)是x的一个邻域.
C3对于w≥1,s≤w,k≥1且(u,v)∈N(x)×N(x),成立下述四个条件期望性质:

C4序列α(n)满足存在一个r>2使得
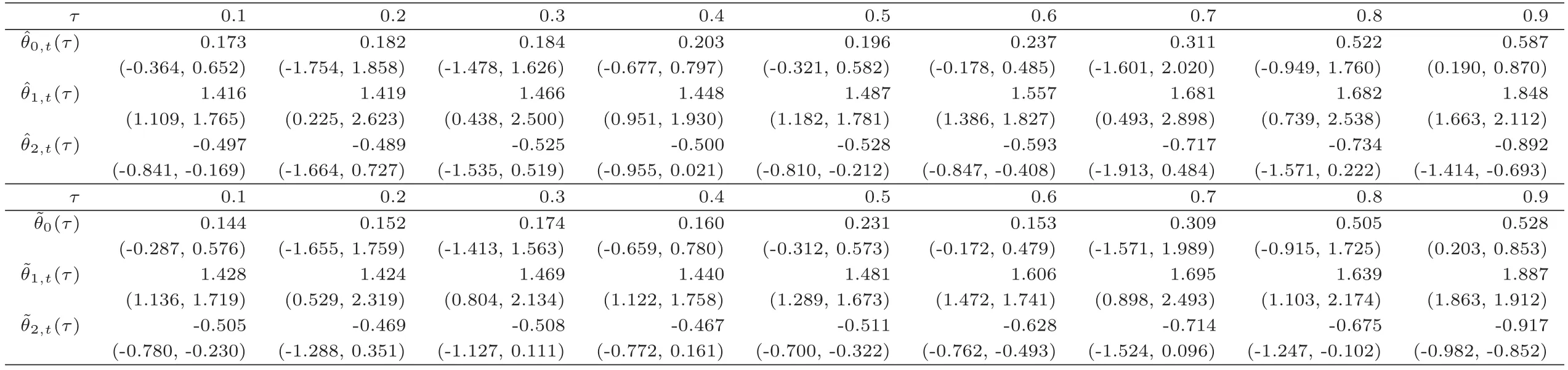
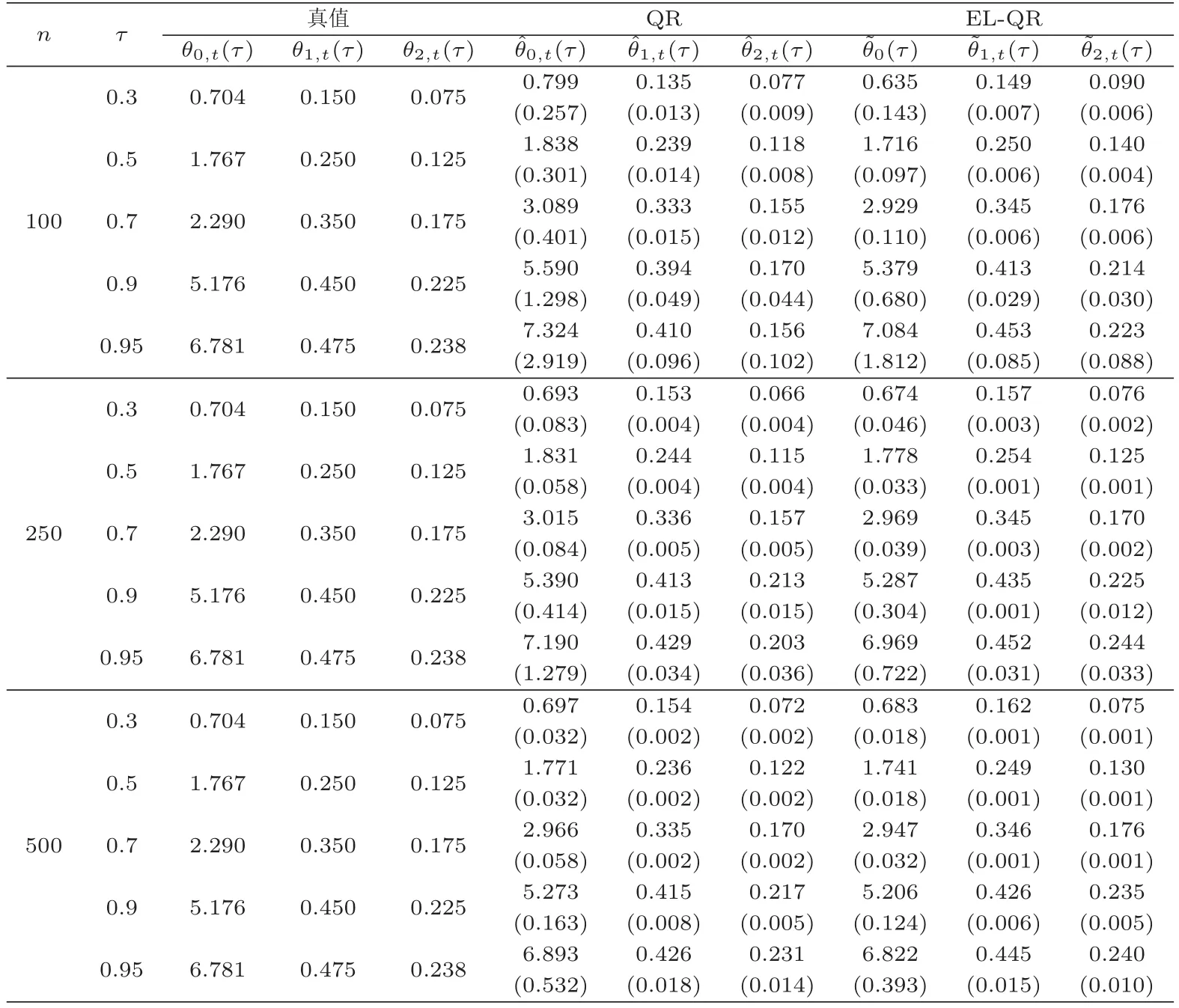
C5{εt}是一列独立同分布的随机变量,均值为0,方差有限.其共同分布函数F作用在集合χ={x:0 C6记条件分布函数Ft−1=P(yt 注记2.1条件C1是经验似然方法中的常规条件(参见文献[18]),用于控制λβ0的随机性质(详见命题2.1).C2以及C3在证明过程中用于处理协方差.对于一般的线性回归模型,当辅助信息函数包含的是独立的随机变量时,这两个条件可以去除.对于相依的数据,条件C4用于证明α-混合序列的渐近性质.C6和C7是得到(A.2)以及(A.3)两个结果所需的技术性条件.这两个条件较弱,不少情况都能够满足.例如:如果随机变量的条件分布是正态分布(或偏态分布),t(或偏t)分布,双指数分布等,条件C6即可满足;如果随机变量的三阶矩存在,条件C7即可满足. λβ0的性质是本文几个主要定理证明的关键,因此下面首先给出命题2.1,它刻画了λβ0的统计性质. 命题2.1假设条件C1-C4成立,λβ0满足kλβ0k=Op(n−1/2). 定理2.1令yt是(4)中定义的平稳时间序列,如果条件C1-C7成立,则 当系数αj,t是常数时,分别定义εt的分布函数与密度为F(x)和f(x),可以得到以下推论: 推论2.1在定理2.1的条件下,如果(4)式中的系数αj,t是常数,那么对一个给定的τ,有 其中Ω与定理2.1中的定义一致. (4)式中模型的表达式可以改写成计量经济中广泛使用的Dickey-Fuller自回归模型 推论2.2在定理2.1的条件下, 其中Ω和Σ1由定理2.1中给出,且 在2.1中假设β是已知的,然而在实际应用中,总体的先验信息往往较难获得,因此需要讨论辅助信息包含未知参数β的情形.当辅助信息中的参数β未知,一个可行的办法是首先对β进行估计.令(7)式中的=argmaxβEL(β),文献[9]证明了在一定的条件下,能够达到最优有效性.因此,将代入权重{ωt}的表达式可得: 其中满足 现在令 注记2.2对于β未知的情形,文献[18]称其为“Auxiliary Model Specification”.由于需要先估计β,自回归系数估计实际上通过两步估计得到. 定理2.2令yt是定义在(4)式中的平稳时间序列,如果条件C1-C7满足,则 其中Ω∗=τ(1−τ)Σ0−ΛΣ2ΛT,Σ0,Σ1以及Λ与定理2.1中的定义一致. 注记2.3注意到Σ1,Σ(β0)是正定的且Σ2是非负定的.与文献[1]中的估计量的渐近性质(5)相比,由于引入了辅助信息h(Zt;β).QAR模型的估计量的协方差分别减少了进一步可见,Λ依赖于h(Zt;β)和τ−I(εt,τ<0)的相关系数,因此h(Zt;β)和τ−I(εt,τ<0)的相关性越强,估计的效率被提升得越明显;反之,如果h(Zt;β)和τ−I(εt,τ<0)是不相关的,估计的效率就不会被改进. 类似的,可以得到下述推论. 推论2.3在定理2.2条件下,如果(4)式中的系数αj,t是常数,则对给定的τ, 其中Ω∗与定理2.2中定义一致. 推论2.4在定理2.2条件下,其中Ω∗和Σ1与定理2.2中定义一致,J由(10)式给出. 回归模型中,Wald检验常用来检验多个模型系数的显著性.考虑如下的q维线性假设检验 其中Γ是一个q×(p+1)维的矩阵,γ是一个q维向量.对QAR模型建立如下(回归)Wald过程Vn(τ): 根据定理2.1,可以直接得到: 定理3.1当假设检验H0成立时,如果定理2.1中的条件都成立,则有 其中Ω和Σ1与定理2.1中的定义一致. 因此,构造相应的Wald检验统计量如下: 并且,给定合适的τ后,yt的条件密度函数的估计由下式给出: 定理3.2在定理2.1的条件下,对某一特定的分位数τ=τ0, 其中表示自由度为q的中心化卡方分布. 对于辅助信息中的参数β未知的,根据定理2.2可以得到下面的定理3.3. 定理3.3令,当线性假设检验H0成立时,如果满足定理2.2中的条件,则有 其中Ω∗以及Σ1与定理2.2中定义一致. 类似的,可以建立如下Wald检验统计量 其中 定理3.4在定理2.2的条件下,对某一特定的分位数τ=τ0, 其中表示自由度为q的中心化卡方分布. 为了展示本文所采用方法的有效性,本节通过有限样本的数值模拟结果,来说明借助辅助信息所得到的模型系数的估计量,其估计效率较传统的分位数回归估计要高.数值模型生成以下二阶随机系数自回归模型: 其中θ0,t=F−1(Ut)(F(·)表示一列随机变量的分布函数),θ1,t=0.5Ut,θ2,t=0.25Ut,且Ut∼U[0,1]. 对任意固定的τ∈(0,1),设定系数分位数的真值分别是θ0,t(τ)=F−1(τ),θ1,t(τ)=0.5τ和θ2,t(τ)=0.25τ. 首先生成一组{y1,···,yN},N=50,000,然后取{y1,···,yN}的一个长度为n的随机子集(n=(100,250,500))来拟合QAR(2)模型,记为{y1,···,yn}. 针对不同的样本量n=100,250,500和τ=0.3,0.5,0.7,0.9,分别用不带辅助信息的一般分位数回归(QR)以及基于经验似然方法的分位数回归(EL-QR)来估计模型(16)的条件自回归系数分位数θ0,t(τ),θ1,t(τ)以及θ2,t(τ).记一般QR估计量,以及EL-QR估计量.每一组模拟都重复1000次,分别计算两个估计量的均方误差(MSE).表1和表2总结了在不同的F设定下,QR估计和EL-QR估计的比较.表格中的数表示对应参数的估计值,括号内表示估计量的MSE.从表1和表2的数据可以看到,每个的MSE都要小于的MSE,即使在样本量很小(如n=100)的情况下也是如此.同时,对于相同的分位数,随着样本量的增加,MSE不断减小.这表明对于QAR模型,本文提出的EL-QR方法的模拟效果要好于一般的QR方法.这归因于EL-QR方法考虑了辅助信息,使得更多的总体信息能够被挖掘出来,且理论上证明了提出的方法能够缩减估计渐近分布的方差.这也意味着传统分位数回归估计量的效率,因为加入了总体的先验信息而被提升了. 本节将文章的方法应用于实例数据的分析,用QAR模型来拟合美国失业率数据.数据分析采用了从1948年-2003年的季度失业率数据,共224个观测且去掉了季节性趋势.文献[1]的研究指出,失业率响应对于经济的正向以及负向效应存在着不对称性.由于失业率数据对于经济的扩张与收缩效应存在的这种不对称性在经济政策的制定中起着十分重要的作用,对其进行深入的研究尤为必要.首先对失业率数据进行单位根检验,结果拒绝原假设,表明序列是平稳的.然后利用AIC准则确定滞后阶数p=2,这与文献[1]中利用BIC准则选出的长度一致.最后建立如下AR(2)模型来刻画失业率的非对称动能, 表1 给定F是偏t分布的分布函数时,QR估计和EL-QR估计的效果比较 表2 给定F是双重指数分布的分布函数时,QR估计和EL-QR估计的效果比较 针对上述模型,通过列表总结了的分位数回归的估计(每0.1为一个单位)及其95%置信区间.表3的上半部分是没有辅助信息的传统分位数估计结果,下半部分是利用本文方法得到的结果汇总.不难发现,利用文中给出的方法所得到的95%置信区间的长度总是小于传统的方法.这表明,通过包含辅助信息的分位数回归方法要优于传统的分位数回归. 表3 美国失业率数据分位数回归估计(每0.1为一个单位)及其95%置信区间(上侧数据和下侧数据分别由传统分位数回归和经验似然方法得到) 定理3.1和定理3.2的结论可以直接从定理2.1,推论2.1以及推论2.2中直接得到.定理3.3以及定理3.4可以从定理2.2,推论2.3以及推论2.4得到.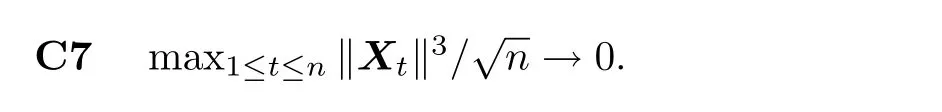

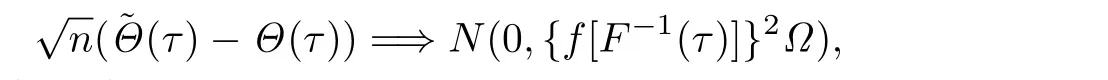
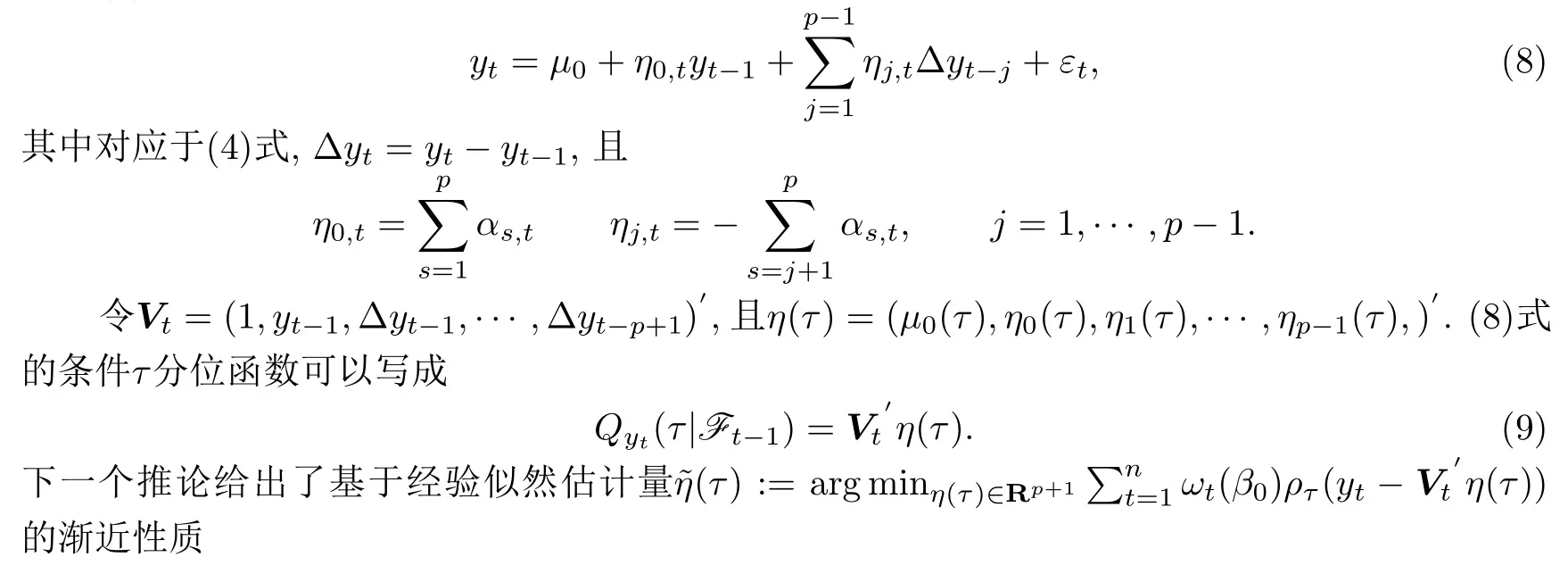

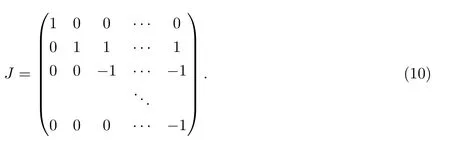
2.2 辅助信息中参数β未知

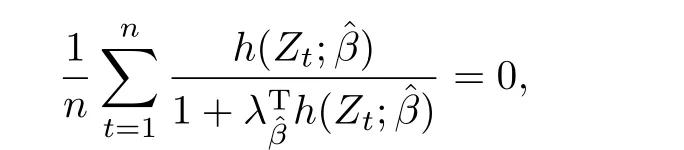



§3 QAR模型的Wald检验


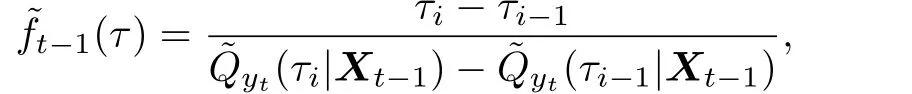


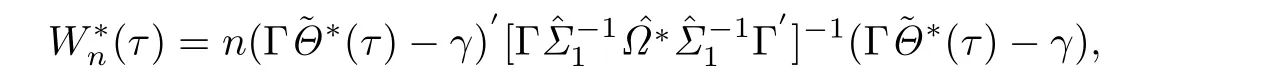
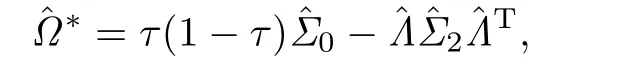
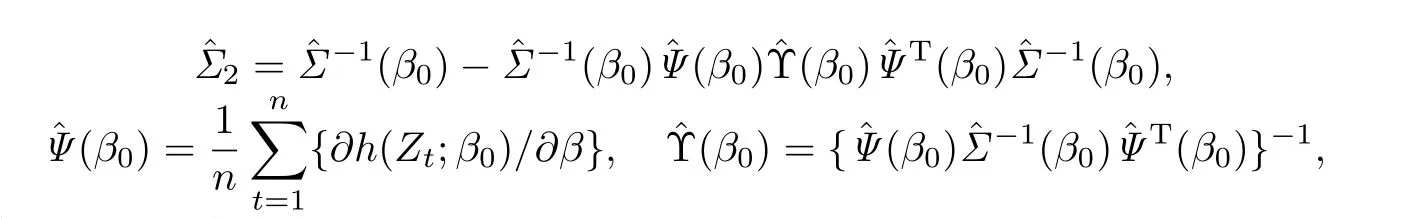

§4 数值模拟与实例数据分析
4.1 数值模拟
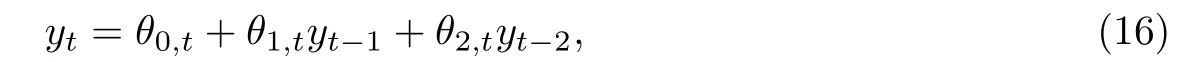
4.2 实例数据应用
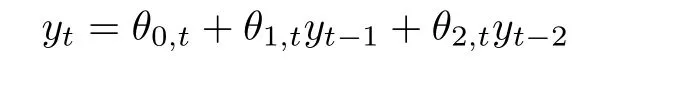

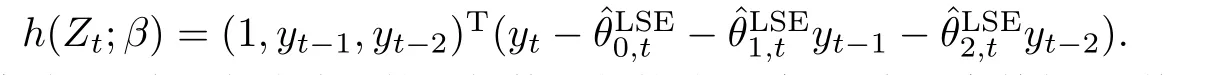
§5 主要结果的证明