函数型聚类分析方法研究
2020-07-07孙利荣卓炜杰王凯利马佳辉
孙利荣, 卓炜杰, 王凯利, 马佳辉
(浙江工商大学统计与数学学院,浙江杭州310018)
§1 引 言
聚类分析是一种完全依据数据集特征的无监督学习方法,没有事先已知的类标签,因此聚类分析的结果很大程度上取决于数据本身的特性.传统的聚类分析常将采集的样本数据视作为一个个向量,然后利用向量进行聚类分析.随着信息技术的高速发展,许多领域都涌现出大量的复杂数据集,随着数据采集频率的加快,数据形式不再仅限于传统的向量形式.比如,工业领域的数控机床的实时监控数据,医学领域的磁共振图数据,气象领域的气温观测数据,金融领域上市公司股价变动的数据等.由于采集速度非常之快,这一系列数据的采集都近似能看作是一个连续的过程,数据之中包含着许多动态的信息,这一类数据通常被视作函数型数据.函数型数据的概念最早由Ramsay在1982年提出[1].不同于传统数据类型,函数型数据的表现主要以曲线为主.
目前,已有很多学者开始使用函数型聚类方法进行聚类分析.例如,Jank和Zhang利用网上竞价的信息,应用函数型聚类方法进行消费者风险评估[2],程豪和苏孝珊应用函数型聚类分析方法将我国31个省按照GDP的发展潜力分成了四个梯队等[3].
现有的函数型聚类方法基本可以分为四类,分别为原始数据直接聚类,基于连续函数的两步串联法聚类,自适应模型聚类和基于距离(相似性)的聚类(见文献[4-6]).例如Boullé将函数型数据化成固定大小的点集,进行密度估计,然后使用贝叶斯模型进行分类[7].Lim等在小波基函数的基础上对多尺度函数型数据进行了聚类[8].李豫使用了多元函数型高斯混合模型对城市空气质量曲线进行聚类分析,充分考虑了多维数据的p个曲线之间的相关关系[9].Martino等使用广义马氏距离对多元函数型数据进行k-means聚类[10].根据函数曲线的相似性测度不同,函数型聚类分析方法主要可以分为基于数值距离的函数型聚类分析方法和基于曲线形态模式的函数型聚类分析方法.
基于数值距离的聚类分析方法基本原理是延续了传统聚类分析中距离度量的思想,衡量的是数据在绝对水平上的相似性.由于数据本身具备函数特征,所以和传统的聚类分析有所区别.函数型聚类分析中距离的计算方式主要有两种:(一)将传统距离计算方式衍生至函数型数据,直接作为相似性度量.王桂明定义了函数型数据的闵科夫斯基距离,马氏距离以及相似系数,并给出了基函数框架下各种距离的计算方法[11].(二)使用基函数展开系数代替函数型数据进行距离度量.王德青等[4]指出基于基函数展开系数的距离度量实则是通过在确定数据的基函数展开方式之后,使用基函数展开系数向量代替传统的离散点向量,根据向量之间的相似性刻画函数的距离.根据基函数展开系数估计的过程中系数是否可变,聚类分析方法可以分为两步法串联聚类以及自适应模型聚类.
基于曲线形态模式的聚类方法是通过函数曲线的形状以及动态特征构造相似性度量进行聚类的一种非参数聚类方法.这种方式主要是通过函数波动的波峰与波谷的波动位置以及波动程度来衡量曲线的动态特征,往往要抓取函数曲线的加速度以及导函数的加速度等,对曲线的可导性要求较高.目前基于曲线形态的相似性度量方法主要有两类:(一)基于导数距离的相似性度量[12],即使用各阶导数曲线来衡量曲线变化率,变化加速度等曲线内在的动态特征.(二)基于极值点的相似性度量,即利用曲线极值点位置衡量曲线的相似性.Ingrassia等提出了两条曲线之间临近极值点的概念,并提出了一种基于曲线极值点符号变化的相似性度量和一种基于临近极值点间时间跨度的相似性度量[13].靳刘蕊提出了一种基于极值点纵横向的相似性度量,使用临近极值点之间的欧式距离来代替临近极值点之间的时间跨度[14].
基于数值距离的相似性度量仅仅能够体现曲线在绝对水平上的差异,无法体现出曲线动态变化的特征.基于曲线形态的相似性度量虽然能够一定程度上反映出曲线的变化特点,但是主要是抓取了曲线变化局部的特征,缺少对曲线之间的整体差异的衡量.目前研究中,对于曲线数值距离和曲线轨迹形态的选择往往是主观决定的.以金融股票价格曲线为例,在对价格曲线进行聚类时,一些做中长期的价值投资者会比较重视曲线之间的整体差异,常使用前者作为聚类方法;而一些短期做波段的投资者比较重视曲线的波动以及波动时点,通常使用后者作为聚类依据.实际上作为投资者,往往需多方面考虑问题,既希望曲线能够在整体上数值距离更加贴近又希望曲线的轨迹能够尽可能接近,但对于两者的侧重点很难把握.因此函数型数据聚类分析方法中需要一种兼顾数值距离和曲线形态的相似性度量,既能从整体上衡量绝对水平的差异,又能从局部上比较曲线的动态变化特征,客观地将基于数值距离的函数型聚类与基于曲线形态的函数型聚类有效结合在一起.
本文首先依据两种相似性度量的特点,提出了一种基于极值点偏差补偿的相似性度量,希冀同时测度函数型数据数值距离和曲线形态的相似性.然后利用基于各种相似性度量的函数型聚类分析方法以及传统的聚类方法分别对中国证券监督管理委员会《上市公司行业分类指引》中的食品类中的24支股票风险因子曲线进行聚类分析,通过比较不同模型的聚类结果,更加直观地体现各种模型的优缺点,并通过聚类结果可视化对比验证本文所提出的相似性度量方法确实达到了兼顾数据距离和曲线形态的效果.最后,为进一步拓展函数型聚类分析方法,提出多元函数型聚类分析方法—函数型熵权法,并利用上证50股票池价格曲线进行聚类分析.结果显示,多指标函数型聚类除了延续了单指标函数型聚类分析的优点,在聚类的性能上比离散的情形有所提升.
§2 函数型数据
函数型数据的采集数据实际上是离散的,带有噪声的高频数据,因此在进行函数型数据分析前需要对采集数据进行预处理,剔除噪声成分,将离散数据进行重构以获得连续的光滑曲线,即从某样本i的一系列观测值(yi1,yi2,···,yiT)0中提取函数特征,得到函数曲线xi(t).因为实际中遇到的函数型数据是离散化的取样,故假设基本模型形式为:

j=1,2,···,T为观测点的个数,ξ(t)为误差项.一般假设其满足经典的回归假设(独立同分布,均值为0,方差为σ2).
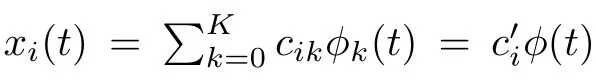
在选择基函数时,通常希望能够选择一个基,通过较少的K个基函数获取对原数据较好的拟合,不仅要在数据特征上对数据进行良好的描述,也要尽可能的计算方便.在函数型数据分析过程中经常要使用到函数的导数或者积分,因此基函数要具有良好的可导性和可积性,常见的基函数有多项式基,傅里叶基,伯恩斯坦基,B样条基,小波(wavelet)基,径向基,函数主成分基,核函数等,根据数据特征的不同,不同的基函数会有不同的拟合效果.本文主要使用B样条基,采用粗糙惩罚法来拟合函数.
B样条基适用于非周期性的数据,本文的研究对象是股市,在观测时间内大多数的股票没有明显的周期性质.因此本文采用B样条基去展开函数,具体展开形式如下:

接下来的一步就是通过基函数展开去估计最近似的系数.估计时通常采用最小二乘法,即最小化如下的平方和:
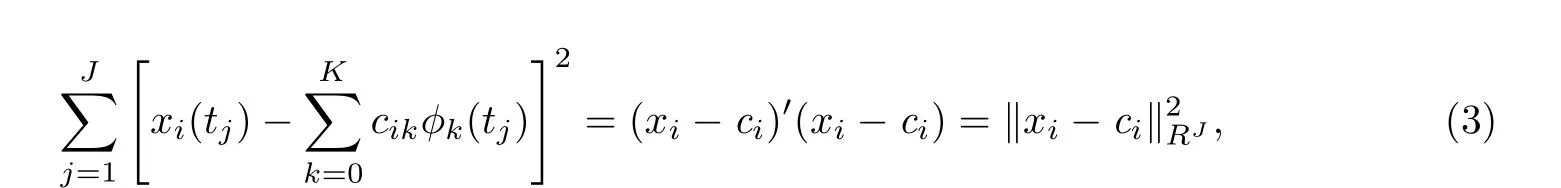
解最小化问题(3),得

或采用最小化惩罚残差平方和(Pernalized Residual Sum of Squares)

其中第二项为粗糙惩罚项(Roughness Pernalty)用来衡量函数xi(t)的平滑程度;m为导数的阶数,通常取2就可以满足一般问题的要求;λ是平滑参数.
说明:光滑参数λ是用来测度函数xi(t)对数据的拟合精度(拟合偏差)与函数本身波动性(曲线样本方差)之间的平衡率.
§3 函数型聚类分析
3.1 基于极值点偏差补偿的函数型相似性度量方法
在基于曲线形态的相似性度量方法中,基于极值点来判定曲线轨迹形态的方法主要是对于极值点间的偏差进行惩罚.显然两条曲线的极值点的位置越接近,最终求得的极值点间距离越小;反之极值点间偏差越大,最终求得的极值点距离也越大.但是极值点间偏差的距离并不能代表曲线偏差的距离,因此该方法只能衡量曲线的局部形态差异,无法体现曲线整体上绝对水平的差异.另外基于数值距离的相似性度量也只是衡量了曲线的绝对水平差异,却没有考虑曲线之间形态的差异.因此,本文将这种对极值点偏差进行惩罚的思想加入曲线数值距离的度量中,提出一种基于曲线极值点偏差补偿的相似性度量.步骤如下:
第一步:极值点描述
求xi(t)的一阶导数,并根据一阶导数求出极值点,并判断是局部极大值点还是局部极小值点.
记函数xi(t)的极值点集合(由小到大按序排列)如下:
对于端点值,若第一个极值点为极大值点,t1则作为极小值点集合的第一个值;若第一个极值点为极小值点,t1则作为极大值点集合的第一个值;若最后一个极值点为极大值点,tT则作为极小值点集合的最后一个值;若最后一个极值点为极小值点,tT则作为极大值点集合的最后一个值.
第二步:临近极值点
对于曲线xi(t)和xj(t),记为中距离最近的点,中距离最近的点,即
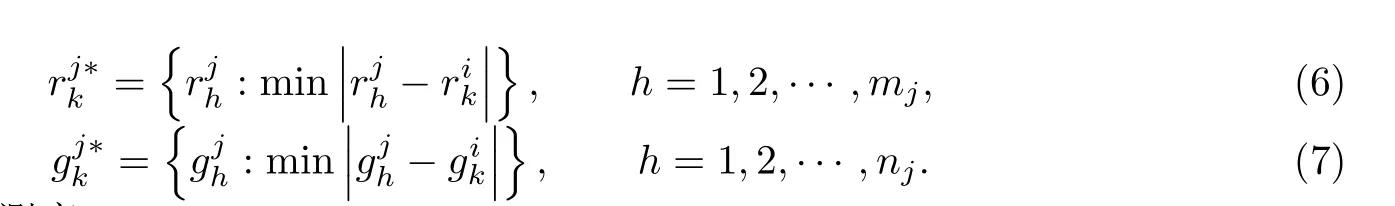
第三步:相似性测度
定义极值点偏差区间:曲线上的极值点与其临近极值点构成的横向区间.以为例,记,极值点的偏差区间为[t1,t2].

定义极值点偏差的距离补偿:将极值点偏差的距离加到两曲线之间的距离中作为由极值点偏差影响而导致的距离补偿.

3.2 聚类模型的选择
本文使用一种改进的K-means++聚类分析方法进行聚类分析.改进的K-means++算法的基本思想为:首先计算所有样本两两之间的距离,选择距离最大的两个样本,将这两个样本作为聚类中心.然后假设已经取了n个不重复样本,则在选取第n+1个样本时,选择与当前n个样本的距离之和最大的样本,以此方法递归出K(类别数)个样本作为初始聚类中心.此算法是针对K-means++中第一个点的随机性进行的改进,思想上仍然延续了K-means++法选择最远组合的思想,但是完全取消了任何随机性,聚类的速度更加迅速.由于函数型数据分析在聚类过程中部分的函数求导以及积分运算设计较大的计算量,为避免运行时间过长,本文选用此法作为初始聚类中心的选择方法.
3.3 几种相似性度量方式的比较
使用不同的相似性度量,聚类结果可能会完全不同.一个简单的例子可直观体现上述几种方法的对比,如图1所示.图中a,b,c,d四条曲线的起始点与终点都相同,变化趋势也是一致的,唯一不同在于极大值点的位置.现在的目标是使用不同的相似性度量方式比较曲线a与曲线b,c,d的相似性.
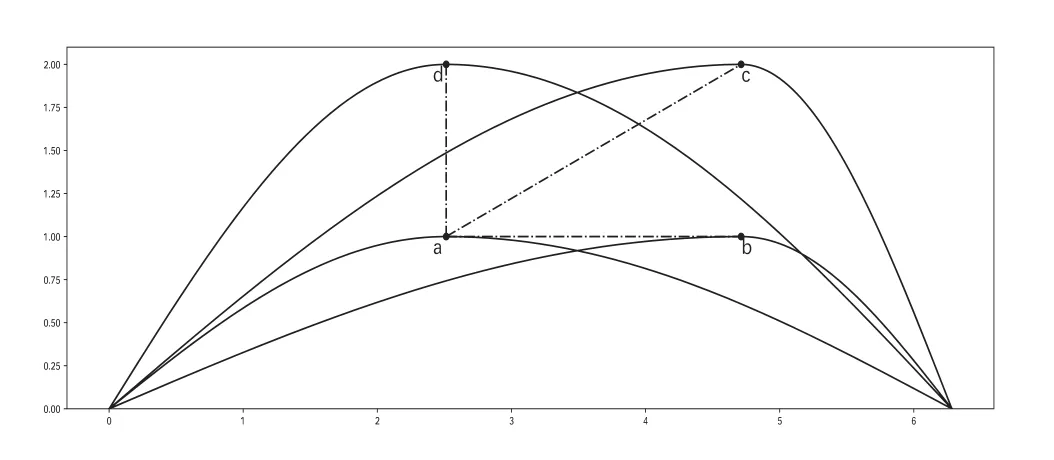
图1 几种相似性度量比较图1.图1的作用是更加直观地展示本章提及的几种相似性度量方法各有的特点,其中位于曲线下方的字母代表该曲线名称.
如果通过基于基函数距离的相似性度量[15]来判断曲线相似性,以绝对距离(曲线间的面积)为例,假设曲线a和曲线b,c,d之间的距离分别为dab,dac,dad,则有dac>dab,dad>dab.而dac与dad之间的大小可以通过计算得到.相比于曲线c和曲线d,曲线b与曲线a更加相似.
如果通过基于极值点符号相似性度量[13]来判断曲线相似性,即通过极值点的极大极小符号序列来判断曲线相似性,由于四条曲线的极值点符号序列完全相同,均为(端点极小,极大,端点极小),则曲线b,c,d与曲线a之间的相似性是一样的,从中能够看出,虽然极值点符号能够代表曲线的极值点波动的规律,但是曲线波动的细节完全没有反映出来,明显有很大差异的b,c,d三条曲线将会被视为相同的.
如果通过基于极值点时间相似性度量[13]来判断曲线相似性,即通过临近极值点的横向距离和来判断曲线相似性,由图1能明显看出曲线b,c,d仅仅在极大值处有差异,假设曲线a和曲线b,c,d之间的相似性度量分别为Dab,Dac,Dad,曲线a和曲线b,c,d的极大值点之间的横向时间跨度分别为dab,dac,dad.由相似性度量的计算公式可以推导出,在本例中,Dab,Dac,Dad的大小关系等价于dab,dac,dad之间的大小关系,显然有dab=dac>dad=0,即相比与曲线b和曲线c,曲线d与曲线a更加相似,而曲线b和c与曲线a的相似性是一致的,从此例中也能够十分明显地体现出该曲线在横向上的时间跨度,但是对曲线在纵向波动的程度上无法进行区分.
如果通过基于极值点纵横向相似性度量[14]来判断曲线相似性,即通过临近极值点的距离和来判断曲线相似性,假设曲线a和曲线b,c,d的极大值点之间的距离分别为dab,dac,dad.显然有dac>dab>dad,相比于基于极值点时间相似性度量,此方法确实能够区分出曲线b和曲线c相对于曲线a的相似性,但是在进行极值点间距离计算时很受横纵轴量纲尺度的影响.
如果通过本文提出的基于曲线极值点偏差补偿的相似性度量来判断曲线相似性,可以更加直观的体现该方法特点,截取图1中的a,b,d三条曲线展示,如图2所示.
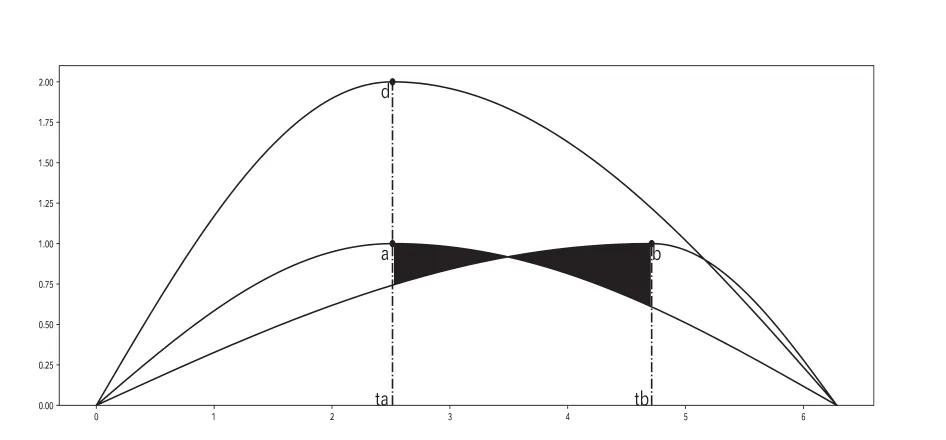
图2 基于极值点偏差补偿的相似性度量说明图2.图2用于展示本文所提出的兼顾数值距离和曲线形态的相似性度量-基于极值点偏差补差的相似性度量,为了图形显示能够更加清晰的描述本文的度量方法,将曲线c隐藏了.其中位于曲线下方的字母代表该曲线的名称.
本文提出的方法不再使用极值点之间的距离作为相似性判定,在计算曲线b与曲线a相似性时,由于曲线b与曲线a的极大值点出现了时间偏差,使用曲线b和曲线a在时间[ta,tb]范围内的距离对曲线b和曲线a之间的距离进行补偿.即在计算曲线b与曲线a的距离时,需要将途中阴影部分的距离额外加入到新的距离计算中,作为曲线形态差异的体现.而计算曲线d与曲线a的相似性时,由于曲线d与曲线a的极值点没有时间偏差,则不需要进行距离补偿.最终通过上文的计算公式进行相似性的比较,基于极值点纵横向相似度测量也能够衡量横纵向的曲线相似.但是使用距离补偿不仅能够将极值点偏差所造成的曲线相似性差异反映出来,而且能够将曲线本身的临近距离考虑进去,且不受横纵轴之间的量纲尺度差异影响.
§4 实证分析
β系数(贝塔系数)是一种风险指数,用来衡量个别股票或股票基金相对于整个股市的价格波动情况.股票的系数不同,收益特征也会显示不同.因此在金融投资领域,投资者经常以β系数的大小作为划分股票类别的基础,进而按照自己的风险偏好选择股票,优化资金配置,更好的进行资产组合管理[16].本文选择了中国证券监督管理委员会《上市公司行业分类指引》(2012年修订)中的食品类中的24支股票作为研究对象,并从国泰安CSMAR数据库中选择了24支股票2018年1月2日至2018年8月3日的风险因子(流通市值加权)数据进行实证分析.
4.1 数据拟合
在对数据进行拟合之前,需要对数据进行无量纲化处理,消除比较对象之间的数量级差异,本文采用归一化.然后选用三次B样条基函数进行数据拟合,并使用误差平方和指标来确定基函数的个数.

图3 基函数个数选择
由图3可知,误差平方和随着基函数个数的变动而变动,并且基函数个数为10时达到最小.因此本文确定使用10个基函数来拟合数据.拟合情况如图4所示.
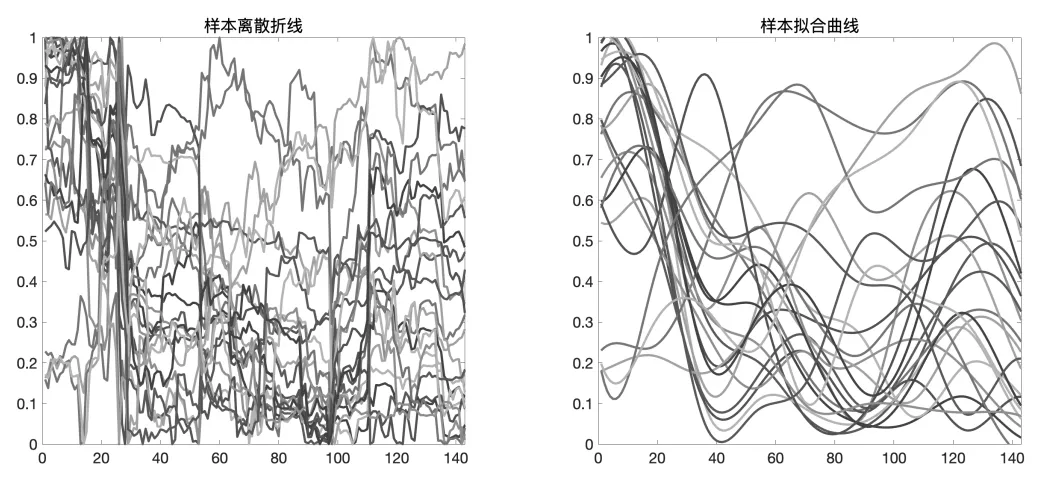
图4 样本离散折线和拟合曲线
从图4可知,样本数据经过函数型拟合后,能够更加清晰地展现股票风险因子的波动特征.在第20期附近,大部分股票的风险因子值都呈现下降趋势;在第130期附近,大多数股票都出现了先上升后下降的上凸形态.但是由于曲线数量过多,曲线之间交杂相错,难以从图中提取更加有效的信息,作为投资者无法从中直接对股票进行有效的类别划分,因此需要进一步的聚类分析.
4.2 聚类模型及参数选取
针对采集的数据分别使用不同的相似性度量方法进行聚类分析,具体包括D1:传统聚类分析方法,即基于采集的离散数据本身的距离度量的聚类分析方法;D2:基于基函数本身的距离度量;D3:基于基函数展开系数的距离度量.D2和D3是两种基于数值距离的函数型聚类分析方法。四种基于曲线形态的函数型聚类分析方法分别为X1:基于曲线一阶导数的距离度量,X2:基于极值点符号的相似性度量,X3:基于极值点的时间相似性度量,X4基于极值点的纵横向相似性度量.本文提出的基于曲线极值点偏差补偿的相似性度量DX,是兼顾数值距离和曲线形态的函数型聚类分析方法.为了统一比较,在离散数据和函数型数据的距离计算中分别选用了传统的欧氏距离以及函数型欧氏距离作为距离度量的方法.由于数据本身的特性以及总聚类样本的个数没有特别大,本文研究了k=3,4,5,6的情形.聚类方法选用了一种K-means++的方法[17],聚类性能的评价使用了轮廓系数[18].
轮廓系数是一种常用的评价聚类性能好坏的方式,是评价每一类的密集与分散程度的指标,轮廓系数的值在-1到1之间,该值越接近于1,说明这一类越紧凑,并远离其他类,这样聚类效果就越好.计算轮廓系数的主要步骤为:
第一步:针对第i个对象,计算对象i到其所属的簇之内所有其他对象的相似性(距离),取均值为ai;计算对象i到其所属的簇之外所有对象的相似性(距离),取均值为bi.记第i个对象的系数为

根据si进行聚类性能对比,si取值范围为[−1,1].si越接近1,表示样本i的聚类越合理;si越接近-1,表示样本i的聚类越不合理.
第二步:取所有对象轮廓系数均值作为该聚类总的轮廓系数,并以此表示聚类性能:

同样s取值范围为[−1,1].s越接近1,表示聚类越合理,s越接近-1,表示聚类越不合理.
4.3 聚类模型性能对比
按照既定的模型以及不同的参数,分别计算各种聚类模型的轮廓系数,结果如表1所示.
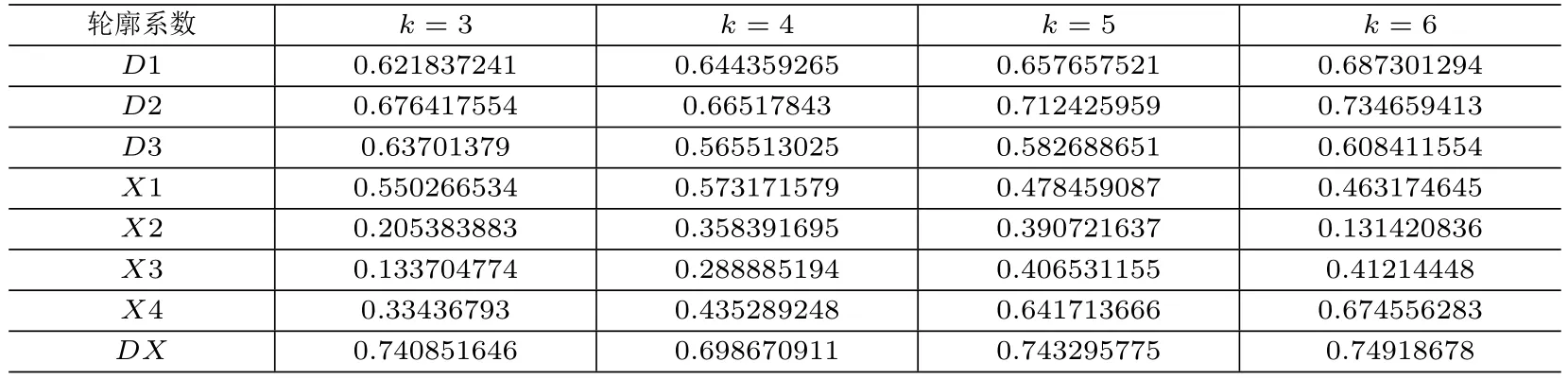
表1 不同聚类个数下不同模型的聚类性能表
针对本文所使用数据,基于曲线形态相似性聚类的四种方法X1,X2,X3,X4中,X1一直保持着较高的聚类效果.随着聚类个数的增加,X4的聚类效果不断提高,超过了X1.在基于数值距离聚类的两种方法中,D2的聚类效果一直优于D3.总体而言,基于距离的相似性度量方法在聚类性能上优于基于曲线形态的相似性度量方法.随着聚类个数的变化,本文提出的曲线极值点偏差补偿的相似性度量DX的聚类效果一直优于其他方法,进一步验证了本文提出的聚类方法的有效性.
4.4 聚类结果可视化对比
为了进一步验证本文提出的基于数值距离与曲线形态的函数型聚类分析方法是否达到既定的效果,本文通过聚类结果的可视化更加直观地展示基于曲线极值点补偿的相似性度量聚类的DX模型的聚类结果与基于基函数本身的距离度量聚类的D2模型的最终聚类之间的差异.本文选择k=3进行聚类分析.
采用本文提出的基于曲线极值点补偿的相似性度量方法进行相似性度量,得到的最终聚类结果如图5所示:
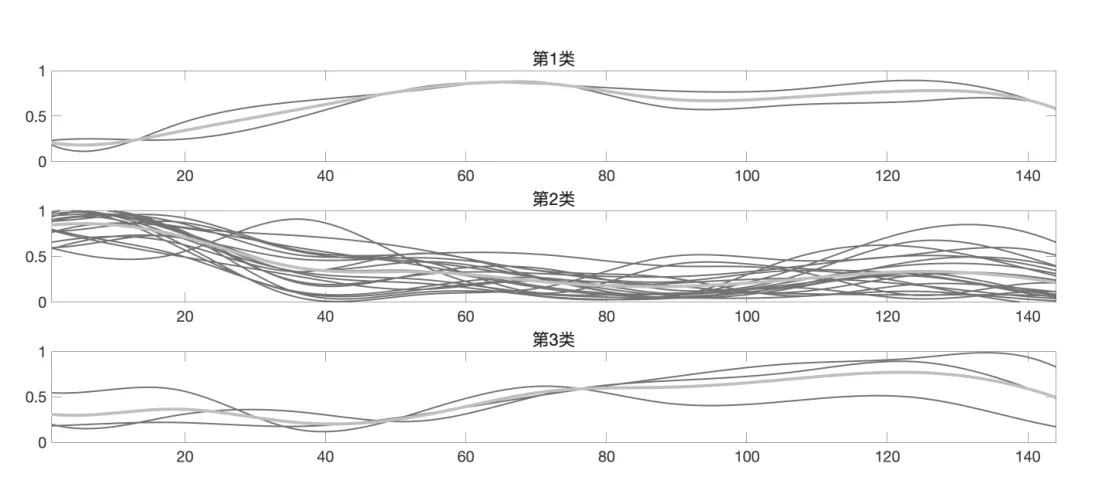
图5 DX模型K=10,k=3聚类结果展现图
DX模型聚类结果中各样本的分类如下:
第一类:花园生物,海天味业
第二类:黑芝麻,三全食品,皇氏集团,双塔食品,佳隆股份,燕塘乳业,桂发祥,上海梅林,莲花健康,安琪酵母,恒顺醋业,青海春天,三元股份,光明乳业,中炬高新,梅花生物,广泽股份,爱普股份,千禾味业
第三类:金达威,伊利股份,桃李面包
采用基于基函数本身的距离度量D2作为相似性度量,得到的最终聚类结果如图6所示:
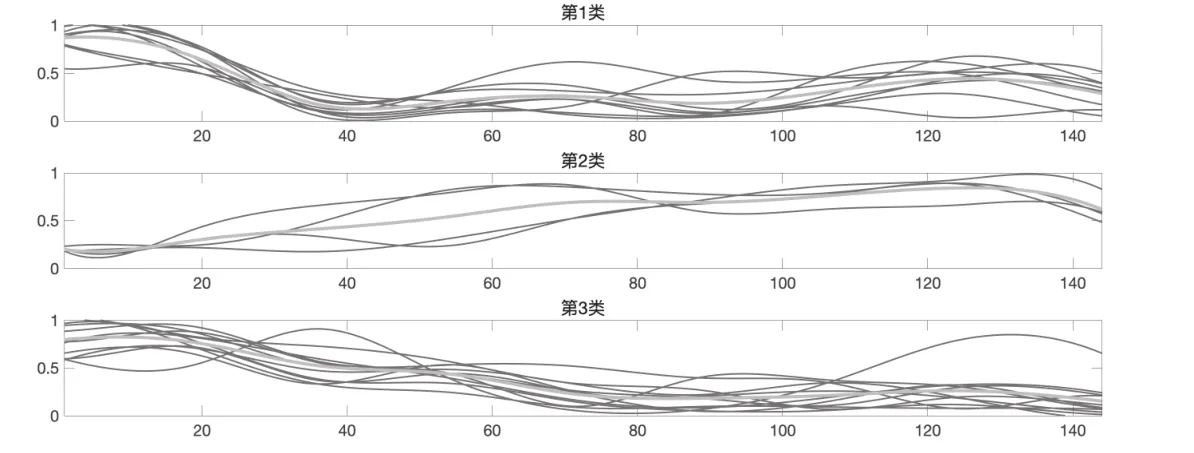
图6 D2模型K=10,k=3聚类结果展现图
第一类:黑芝麻,皇氏集团,双塔食品,佳隆股份,金达威,桂发祥,莲花健康,爱普股份,千禾味业
第二类:花园生物,伊利股份,海天味业,桃李面包
第三类:三全食品,燕塘乳业,上海梅林,安琪酵母,恒顺醋业,青海春天,三元股份,光明乳业,中炬高新,梅花生物,广泽股份
对比D2模型和DX模型具体聚类结果可以发现,DX模型和D2模型均将花园生物,伊利股份,海天味业,桃李面包单独进行分类,说明这4支股票有显著异于其他股票的特征.DX模型将5支显著异于其他股票的股票进一步分类,而D2模型则将其他股票进一步分类.D2模型的分类结果较为均匀,但是聚类效果劣于DX模型.虽然DX模型的操作能获得更好的聚类效果,但是第二类拥有较大的股票样本,对于投资者挑选股票仍具有一定难度.这可能是由于进行函数型聚类时使用的指标过少,因此有必要进行多指标聚类.
从整体的聚类上观察D2模型和DX模型的差异,如图7所示:

图7 D2模型,DX模型聚类中心曲线对比图
图7中分别展示了DX模型与D2模型的聚类中心曲线,从中可以看出DX模型的第一类,第三类与D2模型的第二类聚类中心曲线较为相似;DX模型的第二类与D2模型的第一类,第三类的聚类中心曲线较为相似.DX模型的聚类效果虽然整体优于其他的模型,但是分类结果与D2不好区分,所以需要进一步研究多指标的聚类效果.
§5 多指标函数型数据的聚类分析方法
依据多指标面板数据聚类的思想,多指标函数型数据聚类分析的核心也在于指标的综合.在对多指标函数型数据进行聚类分析时,一种简便的方法是首先对函数型数据的观测值先进行离散形式的多指标综合处理,然后对处理后的数据进行函数型分析.这种多指标函数型数据的聚类分析方法在进行指标综合过程中,会流失部分数据的函数特性.另一种更加合理的方式是先对函数型数据进行拟合,提取函数特征曲线,然后将函数曲线视作整体进行多指标综合.与多指标面板数据不同的是,函数型数据在进行指标综合的过程中,数据是以函数曲线的形式存在的,不能像多指标面板数据一样将数据视作为多个横截面的叠加,而且函数视角下连续时间的权重是难以衡量的,因此通常不考虑权重的时序性,求得综合指标值,即

这里假定指标个数为p,xij(t)表示第j个指标下样本i的拟合曲线,ωj为第j个指标的权重.
基于这样的思想,可以将多指标面板数据指标综合方法拓展至函数型数据领域.许多学者将主成分分析拓展至函数型数据领域并应用于函数型聚类分析,本文将尝试熵权法拓展至函数领域.
熵权法是利用指标的变异性进行定权的一种指标综合方法.熵是一种对系统状态不确定性的度量方法,被评价指标的熵值越小,则说明该指标的变异水平越高,提供的信息量也越大,在综合评价时所起作用也越大,权重相应越大;反之,评价指标提供的信息量少,则权重也相应越小.
5.1 多指标面板数据的熵权法
在多指标面板数据中,通常在计算第i项指标的第j个样本占该指标的比重时,样本不是一个单一的值,而是一个由多个时间点构成的一维向量,此时传统的熵权法无法直接使用,需要新的比重计算方式.
设有n个样本,p个指标,xij(tk)表示指标j下样本i在时间点tk上的观测值,k=1,2,···,T.本节将从多指标面板数据的聚类分析方法出发,研究多指标函数型数据的聚类分析.
第一步:指标正向化处理
第二步:计算第i项指标的第j个样本在观测点tk的值占该指标的比重
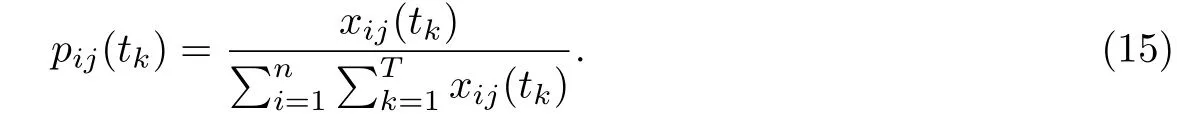
第三步:计算第j项指标的熵值

第四步:计算指标权重

5.2 基于函数型数据的熵权法
由于函数型数据多指标综合的对象是一个函数,因此在计算第i项指标的第j个样本占该指标的比重时,应当将所有的数据点视为一个整体,因此基于离散数据的熵权法中基于点值的计算方式不再适用于函数型数据.利用函数型熵值法求权重的具体过程如下:
第一步:数据预处理.对数据进行正向化处理,然后进行基函数拟合.
第二步:计算第i项指标的第j个样本占该指标的比重函数

第三步:计算第j项指标的熵值和变异程度
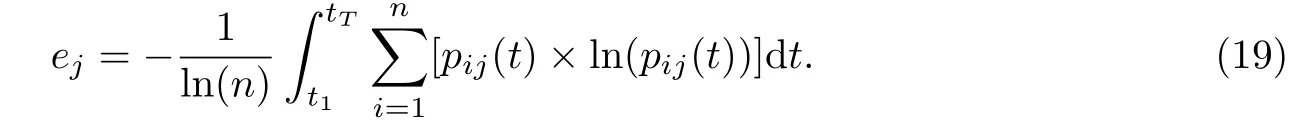
第四步:计算指标权重

5.3 多指标函数型数据的聚类分析方法的实例―上证50样本股量价双指标曲线聚类分析
Robert等[19]指出股市技术分析中最为重要的两个因素就是价格和成交量,因此本文选择价格和成交量两个指标进行聚类分析.首先利用多指标面板数据的熵权法计算离散情形下两个指标的权重,然后选取基函数个数为K=10,15,20,25,30的情形,分别依据不同的K值利用函数型熵权法计算出拟合后两条函数曲线之间的指标权重,具体权重如表2所示:

表2 不同K值下指标权数
从表2中能够看出,同样利用函数型熵权法,函数拟合时选用K值的不同会对指标权重产生微小的差异,而利用函数型熵权法计算的指标权重与利用传统离散情形的熵权法计算的指标权重有着较大的差异.具体使用哪种方式更具优势,需要进一步分析.
为了进一步体现函数型数据分析方法,本文展现了上述股票的价格指标,成交量指标以及量价综合指标的离散折线以及K=10拟合的函数曲线,如图8所示:
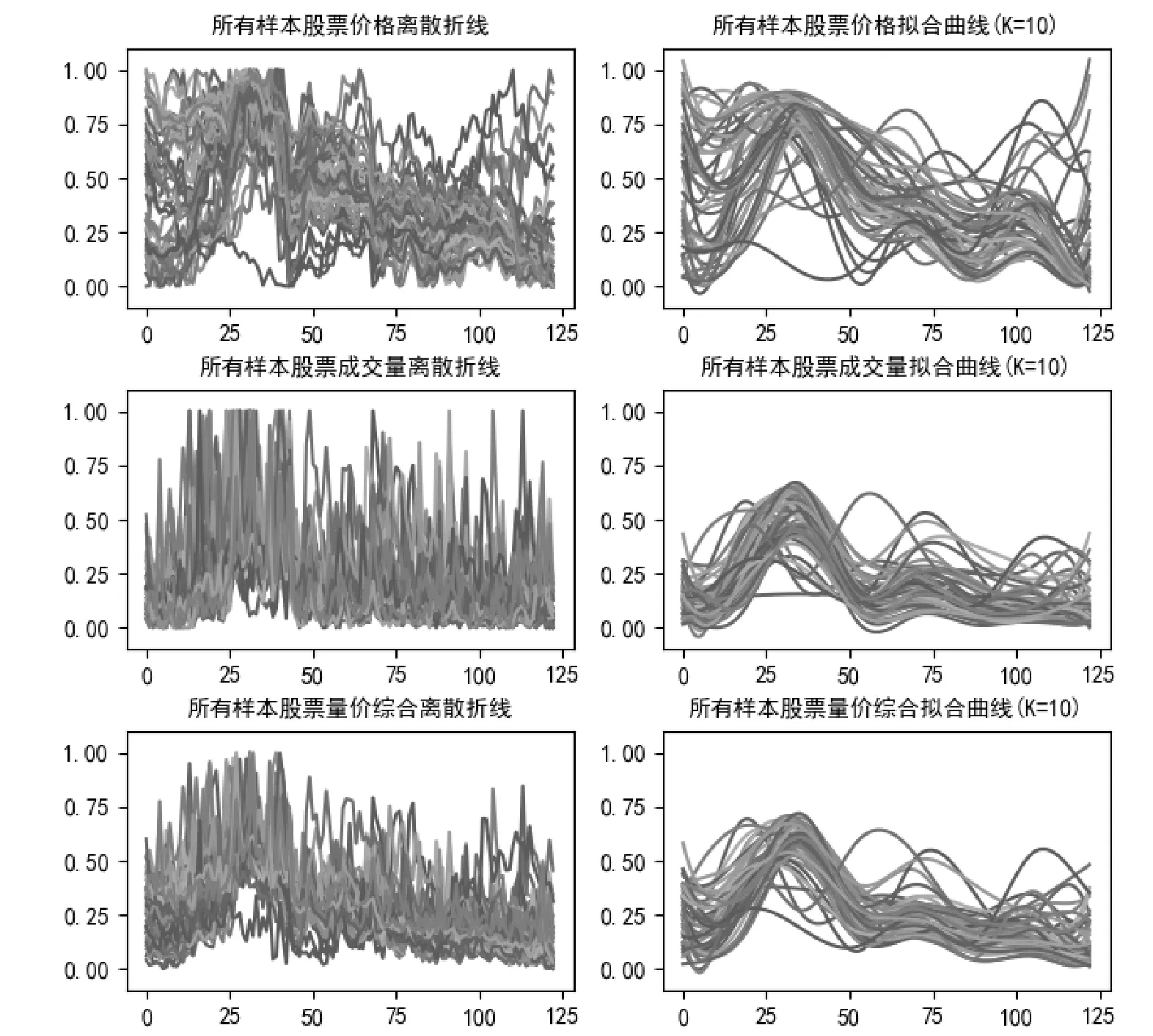
图8 所有股票离散情形和K=10拟合情形下价格,成交量以及综合指标图
聚类分析的相似性度量分别选择了上面实证效果较好度量方式,具体包括基于采集的离散数据本身的距离度量D1,基于基函数本身的距离度量D2以及基于曲线极值点偏移补偿的相似性度量DX.其他参数选择不做变化.
从表3中能够看出,无论使用基于基函数本身距离度量的D2模型还是基于曲线极值点补偿的相似性度量DX模型,最终的聚类效果都比直接使用离散数据距离度量的D1模型要好,说明多指标函数型聚类同样延续了单指标函数型聚类的优点,在聚类的性能上比离散情形有所提高.
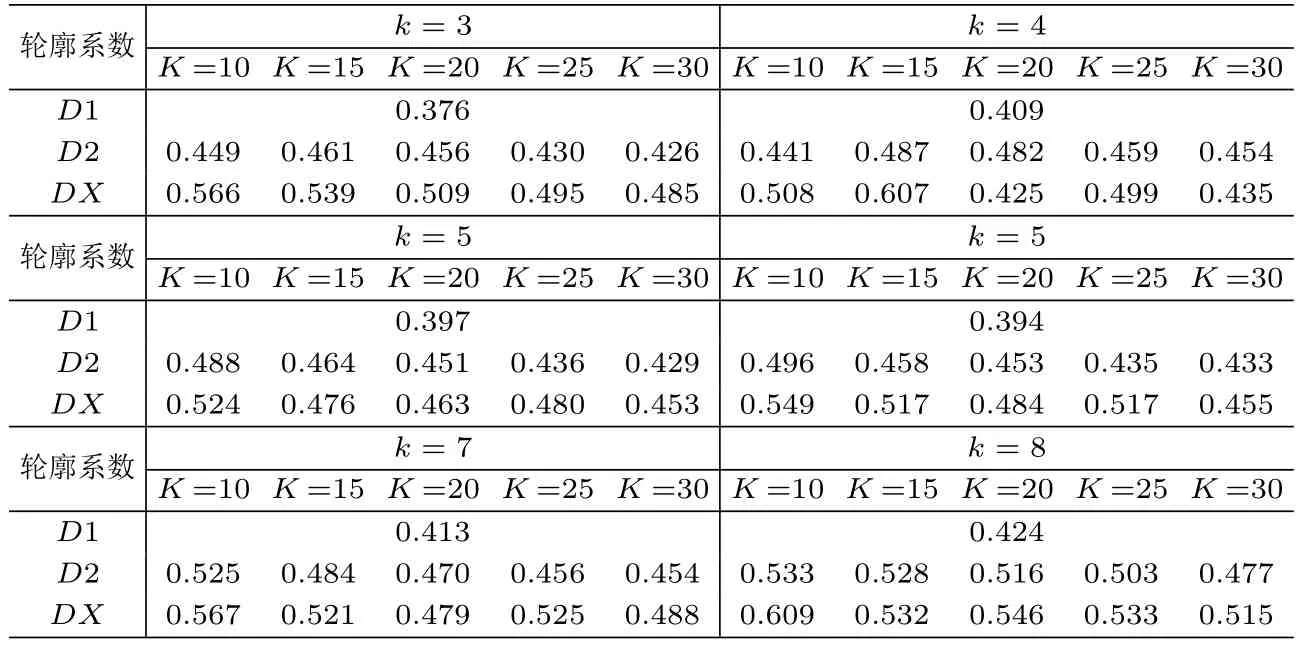
表3 不同参数下不同模型的聚类性能表
§6 结束语
在函数型聚类分析领域,目前的研究普遍侧重于独立研究基于数值距离的相似性测度方法和基于曲线形态的相似性测度方法.本文认为两者对于函数型数据的相似性度量都十分重要,因此提出一种新的相似性度量方法,基于曲线极值点偏差补偿的相似性度量方法.实证结果也说明本文所提的度量方法确实达到了同时测度函数型数据的数值距离与曲线形态的效果.这为函数型聚类分析领域提供了一种有实际应用价值的方法.
对于多指标函数型聚类,由于现有的研究非常至少,本文仅从多指标面板数据聚类的角度出发,将其拓展至函数型领域,将多指标函数型聚类转化为多指标综合问题.对于多指标函数型聚类分析是否有更好的方式,以及对多指标函数型聚类结果的解释问题,还需要作进一步研究.
